Навигация
0 f'(x) > 0
f''(x) >
0 f''(x) < 0
![]() f(a)
a x
f(a)
a x
 3) 4)
3) 4)
f'(x)
<0 f'(x) <0
f''(x)
<0 f''(x) > 0
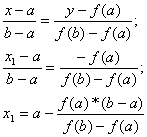 (2.1)
(2.1)
x1(x1,f(x1))
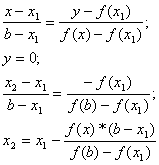
b – неподвижный конец отрезка.
Для случаев 1), 3)
![]()
Для случаев 2), 4)
![]()
Можем ввести некоторую с:
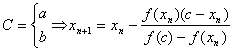 (2.2)
(2.2)
![]() (2.3)
(2.3)
Алгоритм:
1) Вычисляем неподвижный конец отрезка секущих по формуле(2.3)
2) Находим первое приближение к корню по формуле (2.1)
3) Находим первое приближение к корню по формуле (2.2) до тех пор, пока модуль разности двух последних приближений не станет меньше заданной точности. В этом случае, значением корня является последнее приближение.
МЕТОД КАСАТЕЛЬНЫХ
Дано: 1) f(x)![]() C''[a, b];
C''[a, b];
2) f(a)*f(b) < 0;
3) f'(x) и f''(x) знакопостоянны на [a, b];
4) ε, чтобы решить уравнение f(x)=0
![]()
т. х0
y=f(x0)+f'(x0)(x-x0) –
уравнение касательной
a x2 x1 b
y=f(b)+f’(b)*(x-b)
(x1,0) : 0= f(b)+ f’(b)(x1-b)
x1=![]()
x2=![]()
xn+1=![]() (2.4)
(2.4)
Второй подход (метод Ньютона):
![]() -приближение
-приближение
0 = f(![]() ) = f(xn+hn) ≈ f(xn)+f'(xn)*hn
) = f(xn+hn) ≈ f(xn)+f'(xn)*hn
x0 =![]() начальное приближение (2.5)
начальное приближение (2.5)
Алгоритм:
1) По формуле (2.5) находим первое приближение к корню х0 (начальное)
2) По формуле (2.4) находим последующее приближение к корню до тех пор, пока модуль разности двух последних приближений не станет заданной точности. В этом случае корень равен последнему приближению.
МЕТОД ИТЕРАЦИЙ
Дано: 1) f(x)![]() C''[a,b]
C''[a,b]
2)f(a)*f(b)<0
3)f'(x) знакопостоянна
4)ε, f(x)=0
Уравнение f(x)=0 заменяется уравнением вида x=φ(x)
φ(x)=x-f(x)*C (2.6)
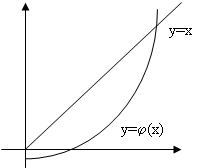 Пока |xn+1-xn|<ε
Пока |xn+1-xn|<ε
φ' >0
Cтроим последователь ![]()
Выбираем ![]()
Находим значение функции
x2= φ(x1), x3= φ(x2)
xn+1= φ(xn) (2.7)
Точка ε, для которой выполняется ε=f(ε), называется неподвижной точкой метода итераций. Очевидно, что эта точка является корнем уравнения f(x)=0.
φ(ε)![]() ε -f(x)* ε
ε -f(x)* ε
0 ![]() f(ε)*C
f(ε)*C
f(ε) ![]() 0
0
Достаточное условие: для того, чтобы метод итераций сходился достаточно чтобы:
1) φ(x)![]() (2.8) - Функция является непрерывной и дифференцируемой на [a,b].
(2.8) - Функция является непрерывной и дифференцируемой на [a,b].
2) φ(x) значения ![]() - является необходимым условием
- является необходимым условием
3) |φ(x)|<1 для всех ![]()
Константа С в формуле(2.6) подбирается таким образом, чтобы функция
φ(x) удовлетворяла условиям сходимости метода итераций.
Скорость сходимости метода Ньютона (касательных) выше сходимости метода секущих (хорд).
ЛЕКЦИЯ №3
МЕТОДЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Общий вид алгебраического уравнения:
а0хn+ а1хn+1+…+ аn-1х+an=0, a0![]() 0 (3.1)
0 (3.1)
n=1: а0х+a1=0, x=![]()
n=2: а0х2+a1x+a2=0, x1,2=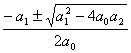
Алгебраическое уравнение n- степени имеет ровно n корней.
Теорема Виета (обобщенная):
xn+![]() xn-1+…+
xn-1+…+![]() x+
x+![]() =0
=0
x1+x2+…+xn=-![]() ;
(3.2)
;
(3.2)
x1x2+x1x3+…+xn-1xn=![]() ;
;
x1x2x3…xn=(-1)![]() ;
;
Пусть все корни уравнения (3.1) действительны, различны и удовлетворяют соотношениям:
|x1|>>|x2|>>…>>|xn| (3.3)
Преобразуем:
![]() x1(1+
x1(1+![]() +…+
+…+![]() )=
)=![]()
![]() x1=-
x1=-![]() ; (3.4)
; (3.4)
Подставим (3.4) : х2=-![]() продолжая получим общую формулу
продолжая получим общую формулу
хk=-![]() , k=1,n (3.5)
, k=1,n (3.5)
Корни уравнения, удовлетворяющие соотношения(3.3), называются отдельными. Задача состоит в том, чтобы по исходному уравнению построить такое уравнение, корни которого будут отделены.
yi=-xim
b0yn + b1yn-1+…+ bn-1y+bn=0 (3.6)
|x1|>|x2|>…>|xn|
Решив уравнение (3.6), корни которого являются отдельными, получим уравнения y1…yn
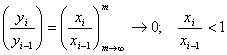 , i=2,n
, i=2,n
Значит |yi-1|>>|xi|
МЕТОД ЛОБАЧЕВСКОГО
Для отделения корней Лобачевский предложил метод квадратирования - способ построения по исходному уравнению нового уравнения, кони которого связаны с корнями исходного следующим образом:
yi=-xi2 (3.7)
Процедура выполнения многократна, пока не достигнем серьёзной разницы модуля разности корней
b0(m)yn + b1(m)yn-1+…+ bn-1(m)y+ bn(m)=0 (3.8)
Пусть уравнение (3.8) получено в результате m-го шага квадрирования.
m=1 b0(1)=a02, b1(1)= a12=2 a0 a2
bk(1)=ak2-2ak-1ak+1+2ak-2ak+2….,k=0,n
При получении bk коэффициента , который рассчитывается как квадрат соответствующего коэффициента ak минус удвоенное произведение соседних коэффициентов с akплюс удвоенное произведение следующей пары соседей , чередуя знаки, пока в число соседних коэффициентов не попадут а0 и аn.
![]() m>1b0(m)=( b0(m-1))2, b1(m)=( b1(m-1))2-2b0(m-1)b2(m-1) (3.9)
m>1b0(m)=( b0(m-1))2, b1(m)=( b1(m-1))2-2b0(m-1)b2(m-1) (3.9)
bk(m)=( b0(m-1))2-2bk-1(m-1)bk-1(m-1)+2bk-2(m-1)bk+2(m-1)
Критерий остановки: bk(m)≈( b0(m-1))2, k=0,n (3.10)
Получим корень: yi(m)=-xi2![]() , i=1,n (3.11)
, i=1,n (3.11)
(3.11)-связь корней, полученных на m-шаге процесса квадрирования с корнями исходного уравнения.
yi на m-шаге : 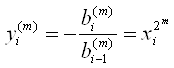 , отсюда
, отсюда
 , i=1,n (3.12)
, i=1,n (3.12)
![]() Знак xi определяется путем подстановки в исходное уравнение. Те коэффициенты, которые будут отвечать за наличие комплексных корней, имеют следующий признак: один или несколько коэффициентов в ходе процесса квадрирования ведут себя неправильно (все остальные коэффициенты →к квадратам предыдущих, а неправильные →к квадратам предыдущих могут менять знак).
Знак xi определяется путем подстановки в исходное уравнение. Те коэффициенты, которые будут отвечать за наличие комплексных корней, имеют следующий признак: один или несколько коэффициентов в ходе процесса квадрирования ведут себя неправильно (все остальные коэффициенты →к квадратам предыдущих, а неправильные →к квадратам предыдущих могут менять знак).
Признак наличия кратных корней: один или несколько коэффициентов → к половине квадрата коэффициента предыдущего шага.
МЕТОДЫ РЕШЕНИЯ СИСТЕМ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
СЛАУ
Методы решения СЛАУ делятся на точные и приближенные. К точным методам относятся метод Гаусса, метод Крамера, метод обратной матрицы .
Существуют приближенные методы: метод итераций, Зейделя и т.д.
Общий вид СЛАУ:
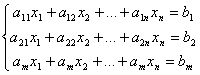 (3.13)
(3.13)
Сколько переменных столько и ограничений на них.
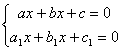 пересечение прямых (точка)
пересечение прямых (точка)
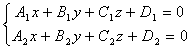 пересечение плоскостей (прямая)
пересечение плоскостей (прямая)
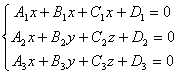 точка пересечения трех плоскостей
точка пересечения трех плоскостей
Т.о. геометрический смысл решения СЛАУ – точка пересечения гиперплоскостей в n-мерном пространстве.
Матрица : =А; B=
=А; B=![]() ; X=
; X=![]() ;
;
Cn*k*Dk*m=Zn*m , An*n*Bn*1=Xn*1![]() AX=B (3.14)
AX=B (3.14)
ЛЕКЦИЯ №4
МЕТОД ГАУССА
Метод имеет прямой и обратный ход. Будем рассматривать процедуру прямого хода метода с выбором главного элемента. Главный элемент – максимальный по модулю элемент матрицы, выбранный на заданном множестве строк и столбцов.
1 шаг: Выбираем в матрице А максимальный элемент по всем строкам и столбцам. Путем перестановки строк и столбцов ставим этот элемент на место а11. Теперь а11- главный элемент.
А→А1→А2→…→Аn
Аn должна будет содержать ниже главной диагонали все нули.
![]() , j =1,n ; b1 =b1/a11
, j =1,n ; b1 =b1/a11
Получим систему вида 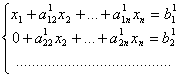
![]() , i=2,n , j=1,n
, i=2,n , j=1,n
![]() Получим А' х=В' и систему
Получим А' х=В' и систему
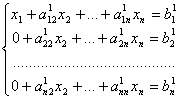
Пусть а221 – максимальный по модулю элемент матрицы А1 по строкам i≥2 и столбцам j≥2. Если это не так, то добиваемся этого путем перестановки строк и столбцов.
А2: 
В2: b12=b11; b22=b21/a221; bi2=bi1-b22-b22ai21
Пусть акк+1 максимальный по модулю элемент матрицы Ак, i≥k, j≥k.
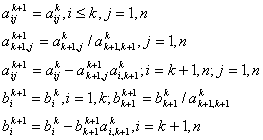
Пусть на некотором шаге k<n элемент ![]() =0, матрица Вк имеет ∞ множество решений. Причем корни х1,…хк являются зависимыми, а корни хк+1,….xn – независимые.
=0, матрица Вк имеет ∞ множество решений. Причем корни х1,…хк являются зависимыми, а корни хк+1,….xn – независимые.
Если хотя бы один элемент bik при i≥k+1 ¹ 0, то решения у системы нет.
Если была получена матрица Аn, то система имеет единственное решение.
Начинается обратный ход метода Гаусса.
МЕТОД КРАМЕРАОпределитель : det A=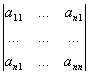
det A= =a11a22-a12a21
=a11a22-a12a21
Минор Hij элемента матрицы aij представляет собой определитель, полученный из матрицы А путем вычеркивания i cтроки и j столбца.
Алгебраическое дополнение Аij элемента аij называется число, равное
Аij=(-1)i+j*Mij
![]()
Способы вычисления определителей
1. Привести определитель к треугольному виду (ниже главной диагонали все элементы=0). Достичь этого можно путем вычитания (сложения) строк определителя, умноженных на некоторое число. При перестановки строк/столбцов знак определителя меняется на противоположный. Определитель треугольного вида равен произведению элементов главной диагонали.
2. Рекуррентный способ основан на том, что определитель равен сумме произведений элементов строки/столбца на их алгебраические дополнения. Т.о. задача вычисления определителя n-го порядка сводится к вычислению n определителей n-1 порядка.
Наиболее целесообразно раскладывать определитель по той строке/столбцу, которая содержит максимальное количество нулей. Алгебраическое дополнение 0-го элемента можно не вычислять.
Пусть дана система уравнений вида Ах=В
Если определитель А=0, то система может решений не иметь, либо иметь бесконечное множество решений.
Если определитель А≠0, то корни системы могут быть найдены следующим образом.
Пусть Ак-матрица, полученная из матрицы А путем замен к-го столбца на матрицу-столбец В. Тогда решение ![]() .
.
Пусть дана система Ах=В и detA≠0.
Умножим обе части системы на А-1:
А-1*Ах=А-1*В→х=А-1*В
Способы нахождения обратной матрицы:
1. Способ основан на методе Гаусса.
Записать матрицу А, а рядом с ней единичную матрицу. Выполняя элементарные преобразования матрицы А, параллельно выполнять те же преобразования над единичной матрицей. Как только матрица А превратилась в единичную на месте исходной единичной матрицы будет обратная к матрице А.
2. Через алгебраические дополнения.
Составить матрицу алгебраических дополнений, в которой на месте aij элементов будут находиться Aij.
Разделить каждый элемент матрицы алгебраических дополнений на detA.
Транспонировать матрицу алгебраических дополнений, т.е. поменять местами элементы, симметричные относительно главной диагонали.
Похожие работы
... с помощью рекурентных соотношений? 104) Приведите конечно-разностные выражения для первой производной. 105) Подынтегральная функция y = f(x) задана таблицейВзяв h = 0,3, вычислить интеграл на отрезке [0,3; 0,9] методом Симпсона. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету ЧИСЛЕННЫЕ МЕТОДЫ Билет № 22 106) Как ...
... затрачивается большой объем памяти для хранения промежуточных данных (u,v,p,…). Метод Рунге скорее удобен для вычисления вручную, но менее актуален в программировании. Если говорить о нахождении более оптимального метода расчета коэффициентов Фурье на ЭВМ, то таким является вышеописанное быстрое преобразование Фурье. Он позволяет сократить количество операций до . В сравнении с вышеописанными ...
... 3. Для функционирования программы необходима операционная система MS DOS 3.30 и выше или полностью совместимой с ней. Исходный текст программы написан на языке программирования высокого уровня Турбо Паскаль версии 7.0 фирмы Borland для DOS и WINDOWS с применением библиотеки Turbo Vision и содержится в файле notebook.pas в форме пригодной к использованию его как текстового документа в среде ДОС, и ...
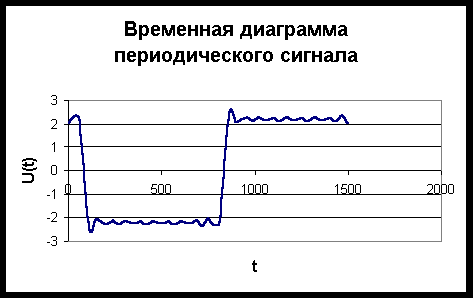
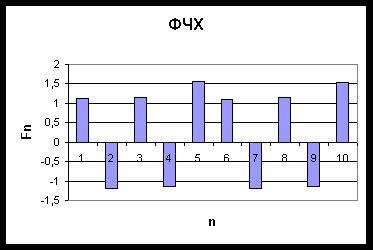
... . Сигнал задан в виде функции времени U(t) , повторяющийся с периодом Т. Требуется выполнить спектральный анализ сигнала и построить графики амплитудного и фазового спектров сигнала. 2.Численные методы расчетов спектральных и временных характеристик периодических сигналов Для расчета спектральных и временных характеристик периодического сигнала используем численные методы, чтобы упростить ...
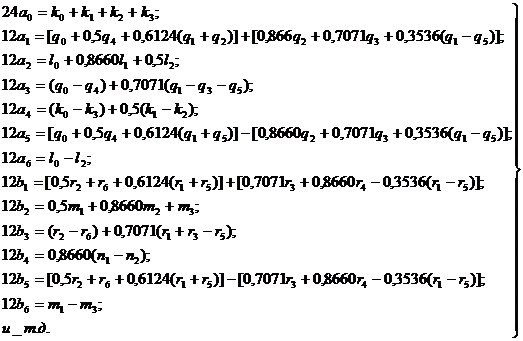
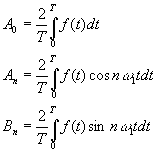
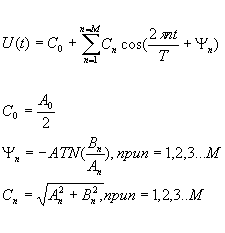
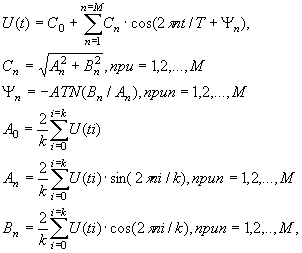
0 комментариев