Навигация
Федеральное агентство по образованию
ГОУ ВПО «Красноярский государственный педагогический университет им. В.П. Астафьева
Факультет математики и информатики
Кафедра математического анализа и методики его преподавания
Курсовая работа
по математическому анализу на тему
«Циклоида»
Выполнила студентка 43 группы
Ковальчук М.В.
Научный руководитель
доцент кафедры мат. анализа и мп
Шатохина М.П
Красноярск 2010
Оглавление
1. Введение
2. Исторические сведения
3. Основные свойства циклоиды
4. Построение циклоиды
5. Геометрическое определение циклоиды
6. Параметрическое уравнение циклоиды и уравнение в декартовых координата
7. Задачи на нахождение частей циклоиды и фигур, образованных циклоидой
8. Заключение
Литература
Введение
Кривая циклоида очень интересна для изучения, однако не так просто найти литературу ей посвященную. В большинстве таких источников циклоида упоминается только вскользь или рассматривается не достаточно полно. Однако она используется при решении различных задач. В виду того, что в школах вводится углубленное изучение математических дисциплин, в скором времени может понадобиться подробная информация о различных кривых, в том числе и о циклоиде. Так же задачи связанные с циклоидой встречаются и в физике и в высшей математике. Поэтому я посчитала данную тему актуальной и интересной для изучения.
Цель работы: описать основные свойства циклоиды, привести решение геометрических задач, связанных с циклоидой.
1. Исторические сведения
Первым кто стал изучать циклоиду, был Галилео Галилей (1564-1642)_ знаменитый итальянский, астроном, физик и просветитель. Он же и придумал название «циклоида» , что значит : «напоминающая о круге». Сам Галилей о циклоиде ничего не писал, но о его работах в этом направлении упоминают ученики и последователи Галилея: Вивиани, Торичелли и другие.
Великий античный философ — «отец логики» — Аристотель из Стагиры (384—322 годы до н. э.), занимаясь логическим обоснованием понятия движения, рассматривал, между прочим, следующий парадокс.
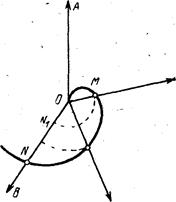
рис. 1
Пусть кружок, изображенный на рис. 1 жирной линией, катится по прямой АВ. Когда кружок этот сделает полный оборот, точка М вернется на прямую АВ и займет положение Мх. При этом, как мы знаем, отрезок ММХ будет равен длине «жирной» окружности. Рассмотрим начерченный кружок с центром О, изображенный тонкой линией. Когда точка М придет в положение М1 этот маленький кружок тоже сделает полный оборот и его точка К придет в положение К1. При этом в каждый момент времени какая-то одна единственная точка маленькой окружности совмещается с единственной же точкой отрезка КК1. Каждой точке окружности соответствует единственная точка отрезка и каждой точке отрезка — единственная точка окружности. Поэтому напрашивается вывод: длина маленькой «тонкой» окружности равна длине отрезка КК1 — ММ1 т. е. равна длине большой («жирной») окружности. Итак, круги различных радиусов имеют окружности одинаковой длины! В этом и состоит парадокс Аристотеля.
Ошибка здесь в следующем. Из того, что каждой точке окружности радиуса ОК соответствует единственная точка отрезка КК1 вовсе не следует, что длина этой окружности равна КК1. Так, например, на рис. 2 точки отрезка АВ приведены при помощи лучей, проходящих через точку D, во «взаимно однозначное» соответствие с точками вдвое большего отрезка СЕ, но никому в голову не придет утверждать, что отрезки АВ и СЕ имеют одинаковую длину! Это же относится не только к отрезкам прямых, но и кривых линий. Парадоксу Аристотеля можно придать следующую, более грубую, а потому и более ясную форму: рассмотрим две концентрические окружности (рис. 3). На них «поровну» точек: соответствующие точки соединены на рис. 3 прямыми линиями (радиусами). И все же никто не станет утверждать, что длины этих окружностей одинаковы.
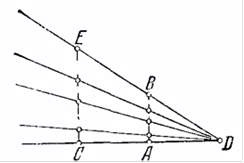
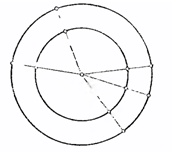
рис 2 рис. 3
Аристотель рассматривал именно то движение, которое через 1900 лет привело Галилея к открытию циклоиды; но он не заинтересовался кривыми, которые вычерчиваются точками окружности катящегося круга.
В самом начале XVII века юный Галилей пытался экспериментально проверить свою догадку о том, что свободное падение — равноускоренное движение. Когда он перенес наблюдения с Пизанской башни в лаборатории, ему стало очень мешать то, что тела падают «слишком быстро». Чтобы замедлить это движение, Галилей решил заменить свободное падение тел их движением по наклонной плоскости, предположив, что и оно будет равноускоренным. Проводя эти опыты, Галилей обратил внимание на то, что в конечной точке величина скорости тела, скатившегося по наклонной плоскости, не зависит от угла наклона плоскости, а определяется только высотой H и совпадает с конечной скоростью тела, свободно упавшего с той же высоты (как вы хорошо знаете, в обоих случаях |v̄|=
Изучив движения по наклонным плоскостям, Галилей перешел к рассмотрению движения материальной точки под действием силы тяжести по ломаным линиям. Сравнивая времена движения по различным ломаным, соединяющим фиксированную пару точек А и В, Галилей заметил, что если через эти две точки А, В провести четверть окружности и вписать в нее две ломаные М и L, такие, что ломаная L «вписана» в ломаную М, то материальная точка из А в В быстрее попадает по ломаной М, чем по ломаной L. Увеличивая у ломаной число звеньев и переходя к пределу, Галилей получил, что по четверти окружности, соединяющей две заданные точки, материальная точка спустится быстрее, чем по любой вписанной в эту четверть окружности ломаной. Из этого Галилей сделал ничем не аргументированный вывод, что четверть окружности, соединяющая пару заданных точек А, В (не лежащих на одной вертикали), и будет для материальной точки, движущейся под действием силы тяжести, линией наискорейшего спуска (позже линию наискорейшего спуска стали называть брахистохроной). Впоследствии выяснилось, что это утверждение Галилея было не только необоснованным, но и ошибочным.
Свойства касательной и нормали к циклоиде были впервые изложены Торичелли (1608—1647) в его книге «Геометрические работы» (1644 год). Торичелли использовал при этом сложение движений. Несколько позже, но полнее, разобрал эти вопросы Роберваль (псевдоним французского математика Жилля Персонна, 1602—1672). В 1634 году Роберваль –вычислил площадь, ограниченную аркой циклоиды и ее основанием. Свойства касательной к циклоиде изучал также Декарт; он изложил свои результаты, не прибегая к помощи механики.
Похожие работы
... материя и движение, и тот метод, который они составляют, дают возможность каждому реализовать свои потенциальные возможности в познании истины. Разработка методики развития диалектико-материалистической формы мышления и овладение аналогичным ему методом познания является вторым шагом на пути решения проблемы развития и реализации возможностей Человека. Фрагмент XX Возможности ...
... обстановке могут заболеть неврастенией – неврозом, основу клинической картины которого составляет астеническое состояние. И в случае неврастении, и в случае декомпенсации неврастенической психопатии существо душевной (психологической) защиты сказывается уходом от трудностей в раздражительную слабость с вегетативными дисфункциями: либо от нападения человек бессознательно «отбивается»больше ...
... различных видах деятельности; • развитии пространственного воображения и пространственных представлений, образного, пространственного, логического, абстрактного мышления школьников; • формировании умений применять геометро-графические знания и умения для решения различных прикладных задач; • ознакомлении с содержанием и последовательностью этапов проектной деятельности в области технического и ...
... дуги. Спиралями являются также эвольвенты замкнутых кривых, например эвольвента окружности. Названия некоторым спиралям даны по сходству их полярных уравнений с уравнениями кривых в декартовых координатах, например: · параболическая спираль (а - r)2 = bj, · гиперболическая спираль: r = а/j. · Жезл: r2 = a/j · si-ci-cпираль, параметрические уравнения которой имеют вид: , [si (t) и ci ...
0 комментариев