Педагогічні програмні засоби довідково-інформаційного призначення

4. Педагогічні програмні засоби довідково-інформаційного призначення.

Ці засоби використовуються для доповнення підручників та навчальних посібників. За формою структурування і подання матеріалу ці засоби можуть бути:

- базами даних (у т.ч. з текстовим і/або мультимедійним поданням навчальної матеріалу) із реляційною, ієрархічною, мережевою моделлю організації даних;

- гіпертекстовими або гіпермедійними системами;

- базами знань, як складовими експертних систем навчального призначення.

За способами зберігання даних довідково-інформаційні системи можуть відповідати зосередженим або розподіленим моделям зберігання даних.

Ефективність здійснення навчального процесу математики у загальноосвітній школі за умов широкого впровадження засобів сучасних інформаційно-комунікаційних технологій (ІКТ) у значній мірі залежить від розуміння вчителями математики шляхів та методів педагогічно-доцільного та виваженого застосування програмних засобів.

Сьогодні існує чимало засобів загального, спеціального, навчального призначення, які можна використовувати у процесі навчання математики, серед них: GRAN, DG, TepM, DERIVE, EUREKA, Maple, MathCAD, MatLAB, Mathematica, Maxima, Reduce тощо. Потенціал застосування цих програмних засобів у навчанні математики в школі висвітлено у роботах Вінниченка Є.Ф., Ганжели С.І., Горошка Ю.В., Грамбовської

Л.В., Жалдака М.І., Крамаренко Т.Г., Костюченко А.О., Ракова С.А., Співаковського О.В., Яценко С.Є. та ін. Більшість вищезгаданих досліджень стосуються застосування програм «сімейства» GRAN, DG, TepM у процесі навчання учнів математики.

Подальшого дослідження потребує визначення шляхів та методів використання систем комп’ютерної математики (DERIVE, EUREKA, Maple, MathCAD, Mathematica, MatLAB, Maxima, SAGE та ін.) у процесі навчання математики в школі.

Системи комп’ютерної математики (СКМ) – програмні засоби задопомогою яких можна досить швидко і якісно виконати чисельні обчислення, аналітичні перетворення, побудувати дво- та тривимірні графіки. Ці засоби сьогодні знайшли широке використання у науці, техніці та освіті. З 90-х років СКМ використовуються в системах середньої освіти Австрії, Словенії, Німеччини, Франції, Італії, Португалії та інших країн.

Вибір СКМ для навчання математики залишається за вчителем. Лідерами серед СКМ є системи Maple та Mathematica. На жаль, на сьогодні вони є комерційними продуктами. Проте, існуючі вільнопоширювані СКМ (до них належать Maxima, SAGE) практично нічим не поступаються згаданим системам. У них реалізовано багато команд для перетворення та спрощення алгебраїчних виразів, диференціювання функцій, обчислення невизначених і визначенихінтегралів, скінченних, нескінченних сум і добутків, розв'язування алгебраїчних і диференціальних рівнянь, їх систем, знаходження границь функцій тощо.

Завдяки значній кількості команд та послуг СКМ для розв'язання досить широкого класу математичних задач з візуалізацією основних етапів розв’язування, ці програмні засоби можна з успіхом використовувати у процесі навчання математики у школі. А саме, для:

• візуалізації абстрактних математичних понять, включаючи можливість анімації графічних зображень;

• виконання громіздких рутинних обчислень з наперед заданою точністю;

• здійснення символьних перетворень для спрощення виразів, доведення тотожностей, тверджень;

• проведення комп’ютерних експериментів, дослідження математичних моделей реальних практичних задач;

• створення електронних документів математичного змісту, що містять текст, графічні ілюстрації, результати обчислень, гіперпосилання на інші документи та ресурси Інтернету тощо.

СКМ можна застосовувати при вивченні таких тем математики: границя числової послідовності, границя функції, похідна функції, дослідження функції на неперервність, монотонність, обернена функція, інтеграл та його застосування, розв'язування різних типів рівнянь, нерівностей, їх систем тощо. Використання СКМ також дає можливість розглянути теми, які часто не розглядаються у процесі навчання математики у зв’язку з необхідністю виконання значного обсягу обчислень (наприклад, при вивченні методів наближеного розв'язування рівнянь).

Використання цих засобів на різних етапах уроку дає змогу активізувати навчально-пізнавальну діяльність учнів, сприяє розвитку їх творчих здібностей, математичної інтуїції, навичок здійснення дослідницької діяльності з використанням сучасних засобів ІКТ.

Можливість проведення комп’ютерних експериментів у середовищі СКМ дає змогу організувати навчання математики з використанням елементів проблемного навчання, дослідницьких підходів у навчанні.

Головною умовою застосування СКМ у процесі навчання математики є те, що воно завжди має бути педагогічно доцільним і виваженим, здійснюватися з метою досягнення поставленої навчальної мети уроку, шляхом встановлення міжпредметних зв’язків курсів математики та інформатики у формі інтегрованих уроків.

Слід також зазначити, що оволодіння вміннями та навичками здійснення обчислень у певній СКМ та використання цих засобів для розв'язування навчальних та прикладних задач є необхідною умовою формування математичних компетентностей учнів, особливо тих, які навчаються у класах з поглибленим вивченням математики і будуть продовжувати навчання на математичних спеціальностях у ВНЗ.

Засоби підготовки електронних документів математичного змісту у середовищі СКМ можуть використовуватися вчителем для створення методичного забезпечення навчання математики на уроках і організації самостійної роботи учнів. Відмітимо, що ефективно використовувати засоби СКМ для розв'язування навчальних задач може лише учень, що розуміє зміст основних математичних перетворень, володіє достатнім рівнем математичної підготовки. Це ще раз спростовує безпідставність суджень деяких вчителів щодо загрози використання СКМ формуванню в учнів математичних навичок. Як показує практика, школярі, використовуючи СКМ як інструмент своєї навчально-пізнавальної діяльності, поступово перетворюються з реципієнтів навчального матеріалу на активних учасників навчального процесу, творців власної системи знань. При високопрофесійній розробці методичного забезпечення, що ґрунтується на принципі педагогічної доцільності застосування СКМ, використання цих програмних засобів у процесі навчання математики, сприятиме утвердженню нової парадигми розвитку математичної освіти, за якою основним її змістом є не опанування певними алгоритмами розв’язування математичних задач, а розуміння і застосування математичних методів дослідження.

Відзначимо такі програми GRAN1, GRAN-2D, GRAN-3D. Вони допомагають організувати евристичну діяльність учнів, у ході якої формуються наступні евристичні уміння:

. спостереження явищ у плані логічних і математичних категорій;

. аналіз фактів, сприйняття їх через призму математичних відносин;

. виділення об'єктів, важливих для пошуку розв’язання задач;

. облік і співвіднесення всіх завдань між собою, з'ясування їхньої погодженості й протиріччя;

. висування різних припущень з обґрунтуванням їхньої можливості (гіпотези);

. передбачення результатів;

. формулювання узагальненого принципу, що пояснює сутність завдання;

. побудова варіантів плану дії, розв’язування;

. пошук асоціацій у зв'язку з об'єктом завдання;

. відшукання нових функцій одного й того ж об'єкта;

. комбінування одних відомих прийомів і способів розв’язування з іншими;

. формулювання й доведення висновків;

. перевірка правильності виконаних дій;

. перевірка повноти й достатності доказів;

. зіставлення результатів з еталонними, нормативними.

Одним із засобів візуалізації задачі та її розв'язку, який робить діалог учня та вчителя більш доступним є педагогічний програмний засіб Gran1. За допомогою Gran1 школярі можуть будувати та аналізувати функціональні залежності явного у(х) та неявного 0(х,у) видів, які задані в декартових чи в полярних координатах, параметрично, таблично. Модифікований Gran1 дозволяє введення і одночасне оперування в програмі дев'ятьма параметрами Р1, Р2, ...Р9, що відкриває нові можливості для реалізації навчання математики. При створенні об'єкта „функція" аналітичний вираз може містити кілька параметрів. В ході дослідження змінюють поточний параметр рухаючи бігунок з певним кроком в заданих межах (Міп-Мах).

Використання ІКТ, а зокрема Gran1, у навчанні математики дозволяє зробити доступнішими для сприйняття абстрактні математичні об' єкти та методи, здійснювати індивідуальний підхід в навчанні, посилює мотивацію, підвищує ефективність процесу навчання математики; створює умови для розвитку творчого мислення та уяви.

Лабораторне заняття №1

З курсу «Застосування ІКТ у навчанні математики»

Тема. Педагогічний програмний засіб GRAN 1.

Навчально-матеріальне забезпечення. Персональні комп’ютери, програмне забезпечення Windows XP, ППЗ GRAN1.

Мета роботи. Отримати навички роботи з педагогічним програмним засобом GRAN1.

Завдання:

1.  Виконати завдання.

2.  Зберегти електронну версію отриманих результати.

3.  Оформити звіт.

Звіт містить такі розділи:

-  Титульний аркуш.

-  Завдання роботи.

-  Письмовий опис дій по виконанню завдань.

-  Отримані результати.

Для роботи у програмі нам знадобляться деякі відомості.

1. Для того щоб створити нову функцію клікніть мишкою на кнопку у вікні «Список об’єктів» та виберіть ту функцію, яка вам потрібна. Потім клацніть правою кнопкою миші у цьому вікні і виберіть «створити».

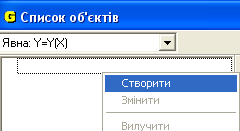
Рис.1 Рис.2

2. Для того щоб побудувати графік натисніть кнопку

3. Для того щоб побудувати пряму х = к задаємо її як ламану, координати точок (к, в) (к, -в), в – будь яке число.

4. Для того щоб знайти площу поверхні та об’єм тіла навколо осі клацніть мишею на кнопку «Операції», виберіть інтеграл, а потім виберіть навколо якої осі відбувається обертання.

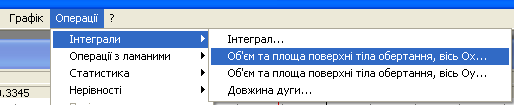
Рис.3

Примітка. Для того щоб записати |х| у програмі вводимо функцію Abs(x), щоб ввести  застосовуємо функцію Sqrt(x).

Практичні завдання

1.  Знайти об’єм тіла та площу повної поверхні тіла, утвореного обертанням навколо осі Ох функції  та прямими у= 0 та х = 3 .

2.  Знайти об’єм тіла, утвореного обертанням навколо осі Ох функції  і прямими у = 0, х = 0, х =

3.  Знайти об’єм тіла та площу повної поверхні тіла, утвореного обертанням навколо осі Ох функції , у = 0, х = 2, х= 1.

4.  Знайти площу повної поверхні тіла, утвореного обертанням навколо осі Ох функції  у = 0, х = 0 , х = /2.

5.  Знайти площу повної поверхні тіла, утвореного обертанням навколо осі Оу функції , у = 0, х = 0.

6.  Знайти об’єм тіла та площу повної поверхні тіла, утвореного обертанням навколо осі Оу функції  та у = 0.

7.  Знайти об’єм тіла та площу повної поверхні тіла, утвореного обертанням навколо осі Оу функції  та у = 0

8.  Знайти об’єм тіла та площу повної поверхні тіла, утвореного обертанням навколо осі Оу функції  та .

9.  Розв’язати нерівність >.

10.Побудувати графік функції

11.Побудувати графік функції

12.Побудувати графік функції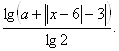

13.Побудувати графік функції .

14.Вкажіть, скільки дійсних коренів має рівняння

15.При яких значеннях параметра а нерівність <0.

16.Обчислити інтеграл .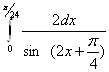

17.Обчислити інтеграл .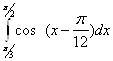

18.Обчислити інтеграл .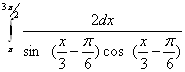

19.Обчислити інтеграл .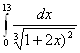

20.Обчислити інтеграл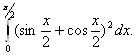

Розв’язання вправ

1.  Знайти об’єм тіла та площу повної поверхні цього тіла, утвореного обертанням навколо осі Ох функцї  та прямими у = 0 та х = 3 .

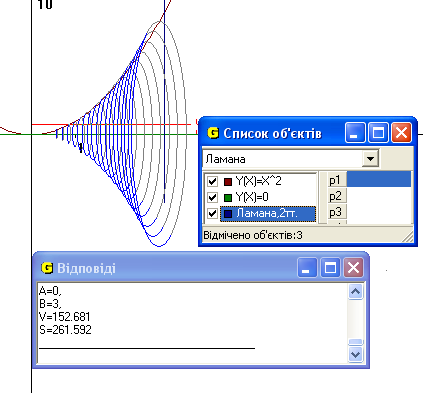
Рис.4

Відповідь: об’єм 152.682 од.куб., площа повної поверхні 261.592 од.кв. тіла утвореного обертанням навколо осі Ох функції  та прямими у = 0 та х = 3 (Рис4).

2.  Знайти об’єм тіла, утвореного обертанням навколо осі Ох функції  і прямими у = 0, х = 0, х =

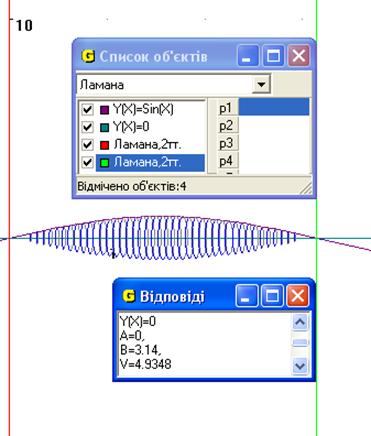
Рис.5

Відповідь: об’єм тіла утвореного обертанням навколо осі Ох функції  і прямими у = 0, х = 0, х =  дорівнює 4.9348 од.куб (Рис.5).

3.  Знайти об’єм тіла та площу повної поверхні тіла, утвореного обертанням навколо осі Ох функції , у = 0, х = 2, х = 1.

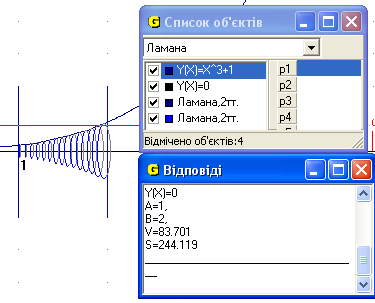
Рис.6

Відповідь: об’єм 83.701 од.куб. та площа повної поверхні 244.119 од.кв. тіла, утвореного обертанням навколо осі Ох функції , у = 0, х = 2, х=1(Рис.6).

4.  Знайти площу повної поверхні тіла, утвореного обертанням навколо осі Ох функції  у = 0, х = 0 , х = /2.

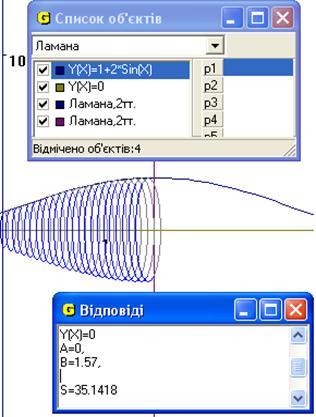
Рис.7

Відповідь: площа повної поверхні тіла, утвореного обертанням навколо осі Ох функції  у = 0, х = 0 , х = /2 дорівнює 35.1418 од.кв (Рис.7).

5.  Знайти площу повної поверхні тіла, утвореного обертанням навколо осі Оу функції , у = 0, х = 0.

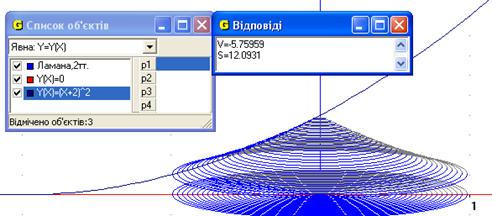
Рис.8

Відповідь: площа повної поверхні тіла, утвореного обертанням навколо осі Оу функції , у = 0, х = 0 дорівнює 12.1 од.кв (Рис.8).

6.  Знайти об’єм тіла та площу повної поверхні тіла, утвореного обертанням навколо осі Оу функції  та у = 0.

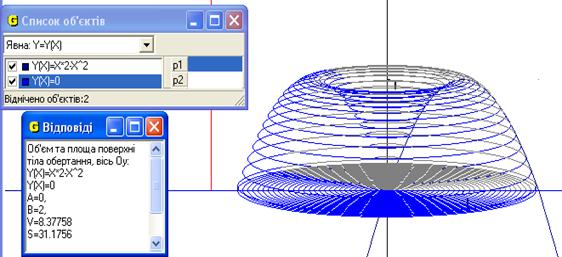
Рис.9

Відповідь: об’єм тіла 8.38 од.куб. та площ повної поверхні тіла, утвореного обертанням навколо осі Оу функції  та у = 0 31.18 од.кв (Рис.9).

7.  Знайти об’єм тіла та площу повної поверхні тіла, утвореного обертанням навколо осі Оу функції  та у = 0.

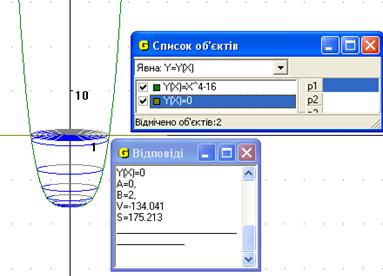
Рис.10

Відповідь: об’єм тіла 134 од.куб. та площа повної поверхні тіла, утвореного обертанням навколо осі Оу функції  та у = 0 175.2 од.кв (Рис.10).

8.  Знайти об’єм тіла та площу повної поверхні тіла, утвореного обертанням навколо осі Оу функції  та .

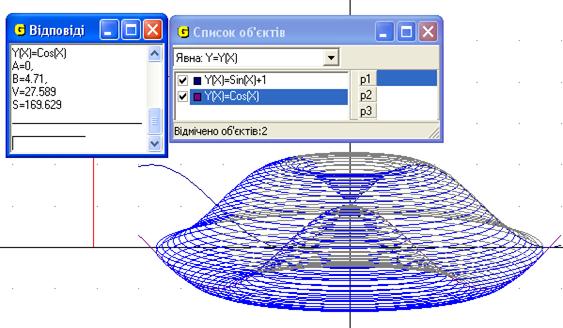
Рис.11

Відповідь: об’єм тіла 27.59 од.куб. та площа повної поверхні тіла, утвореного обертанням навколо осі Оу функції  та  дорівнює 169.63 од.кв (Рис.11).

9. Розв’язати нерівність >.

Будуємо графіки функцій f(x)= i g(x)=.(Рис.12)

 На екрані бачимо, що графіки функцій f(x) та g(x) перетинаються у трьох точках x = − 1; x = 0 та x = 2 . Перевіряємо чи є ці числа коренями рівняння =.

З’ясовуємо що розв’язками нерівності f(x)> (<) g(x) будуть ті значення аргументу, при яких графік функцій f(x) знаходиться вище (нижче) графіка функцій g(x). За допомогою графіка приходимо висновку, що задана нерівність виконується, якщо x ∈ (− ∞ ; − 1 ) ∪(− 1; 0 ) ∪(2; +∞ ).

Отже, маємо розв’язок: x ∈ (− ∞ ;−1) ∪(− 1; 0 )∪ (2; + ∞ ).

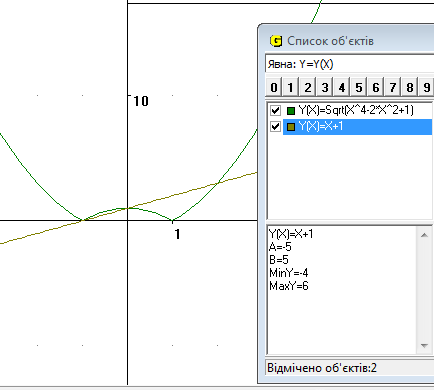
Рис.12

10. Побудувати графік функції

Для цього задаємо тип функції «неявна», а – задаємо як Р1. Змінюючи значення параметру за допомогою повзунку або вводячи значення Р1 з клавіатури ми бачимо як змінюється радіус кола (Рис.13.1). Якщо значення Р1 більше нуль або дорівнює 0, то порушується умова (Рис.13.2).

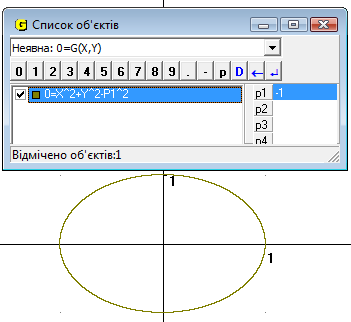
Рис.13.1

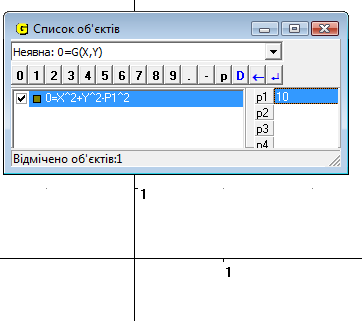
Рис.13.2

11. Побудувати графік функції

При початкових значеннях Р1=0 та Р2=0 ми отримуємо симетричну відносно вісі Оу фігуру, яка проходить черех початок координат (Рис.14.1). Якщо змінювати параметр Р1 (не змінюючи Р2) то ми бачимо як порушується симетрія, а функція все одно проходить через початок координат (Рис.14.2). Якщо змінювати параметр Р2 (не змінюючи Р1) ми бачимо, що симетрія не порушується, але відбуваеться ковзання графіку вздовж осі Оу (Рис.14.3). Якщо змінювати обидва параметри Р1 та Р2, то порушується і симетрія, і відбувається рух вздовж осі Оу.

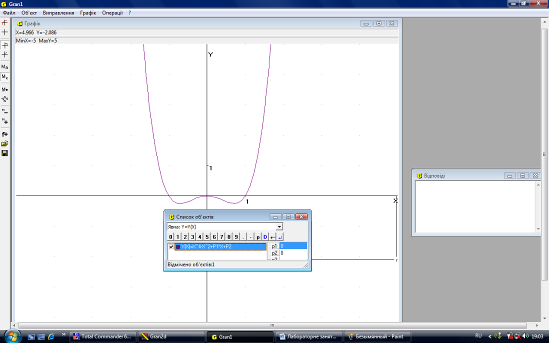
Рис.14.1

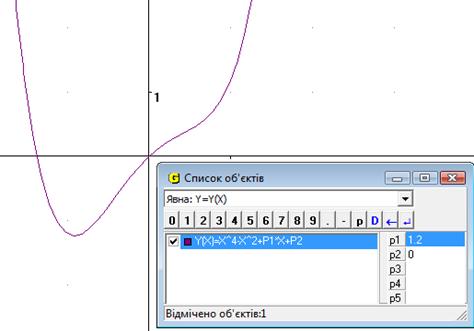
Рис.14.2

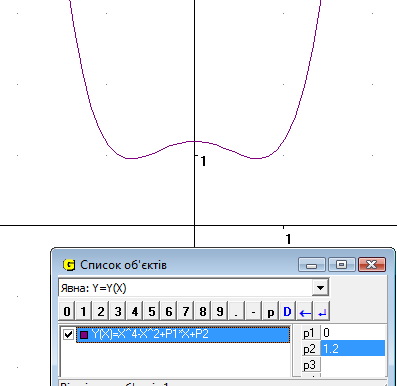
Рис.14.3

12.   Побудувати графік функції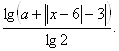

Якщо надати початкове значення Р1 = 0, то ми отримуємо розривну функцію (Рис.15.1). Якщо збільшувати значення параметра, то бачимо, що функція не має точок розриву, а при великому збільшенні Р1 не перетинає вісь Ох і піднімається вздовж Оу (Рис.15.2). Якщо ж навпаки зменшувати значення Р1, ми бачимо, що графік губить одну свою частину і рухається у ІІІ чтверть (Рис.15.3).

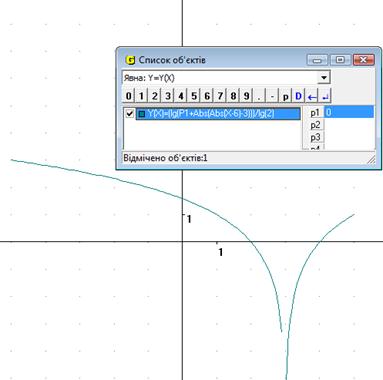
Рис.15.1

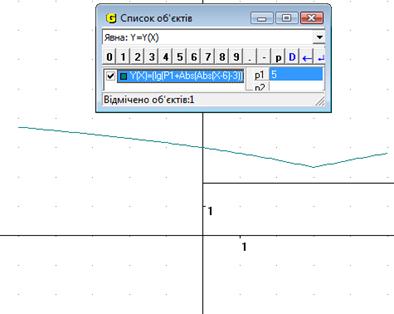
Рис.15.2

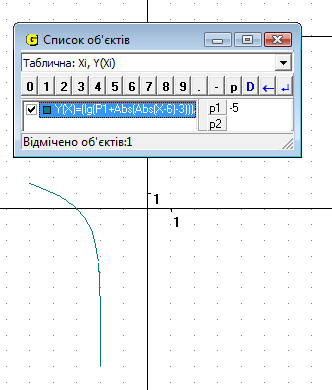
Рис.15.3

13.   Побудувати графік функції

При початкових значеннях Р1 та Р2 ми бачимо, що графік функції складається з 2х частин і знаходиться у нижній частині сітки координат. При зміні Р1 відбувається зміна графіка (випуклість або вогнутість) (Рис.16.1), при зміні Р2 відбувається рух вздовж осі Оу (Рис.16.2). При зміні обох параметрів відбувається і рух вздовж осі ОУ, і зміна графіку (Рис.16.3).

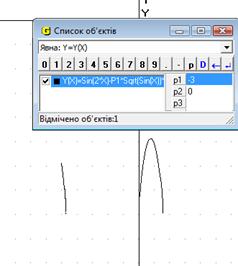
Рис.16.1

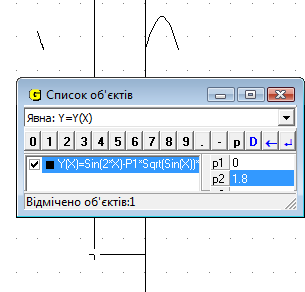
Рис.16.2

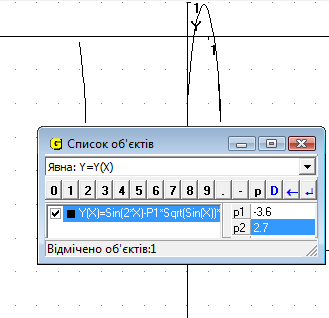
Рис.16.3

14.   Вкажіть, скільки дійсних коренів має рівняння .

 Виконавши найпростіші рівносильні перетворення, маємо рівняння  будуємо у ППЗ «GRAN1» графіки функцій  та  бачимо, що вони перетинаються лише у двох точках (x = 0; x = 2) і робимо висновок, що рівняння має два корені.

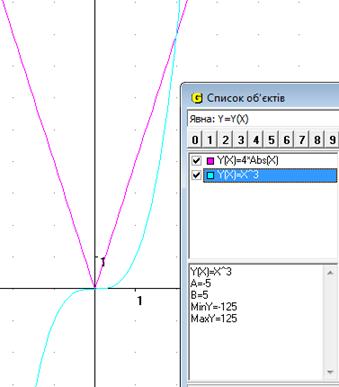
Рис.17

15.   При яких значеннях параметра а нерівність <0.

Треба побудувати графік функції f ( x) = а cos(sinx) та, змінюючя значення параметра а, з’ясувати, при яких значеннях параметру графік функції f(x) лежить вище осі Ох.

Будуємо у ППЗ «GRAN1» графік функції f (x) = а cos(sinx) і аналізують поведінку графіка цієї функції в залежності від значення параметра а.

Висновок. Нерівність має розв’язки при а < 0.

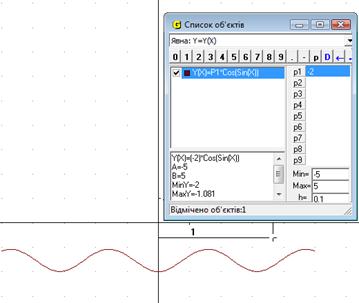
Рис.18.1

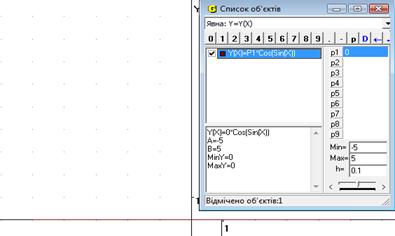
Рис.18.2

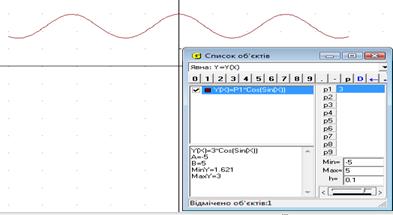
Рис.18.3

16.   Обчислити інтеграл .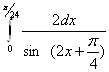

Спочатку створюємо функцію, малюємо графік. Тепер вибираємо вкладку Обчислення – Інтеграл.Отже значення інтеграла І=0.33 од (Рис.19).

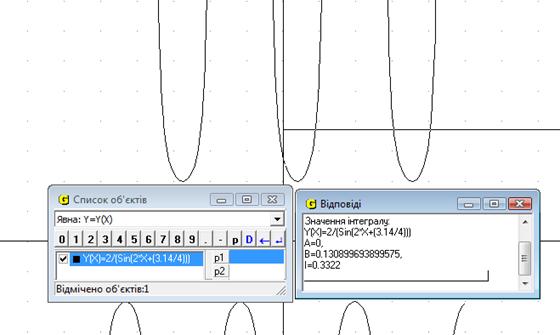
Рис.19

17.  Обчислити інтеграл .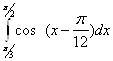

Як і в попередньому прикладі створюємо функцію та обчислюємо інтеграл. Відповідь: 0.26

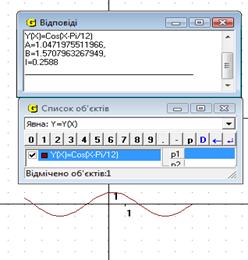
Рис.20

18.  Обчислити інтеграл .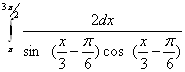

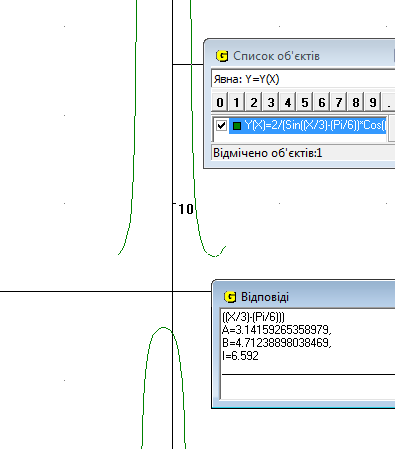
Рис.21

Відповідь: І=6.53 од (Рис.21).

19.  Обчислити інтеграл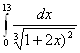

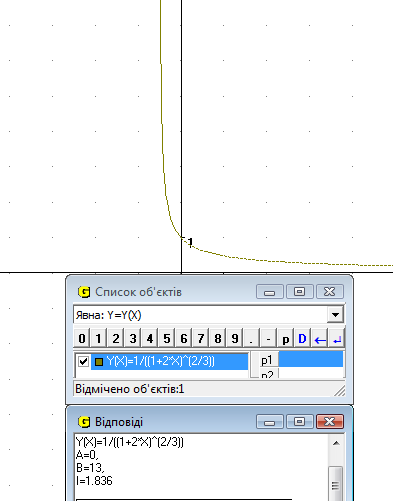
Рис.22

Відповідь: І=1.84 од (Рис.22).

20.  Обчислити інтеграл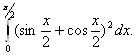

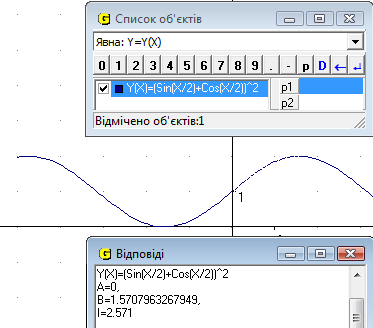
Рис.23

Відповідь: І=2.57 од (Рис.23).

Лабораторне заняття №2

З курсу «Застосування ІКТ у навчанні математики»

Тема. Педагогічний програмний засіб GRAN 2

Навчально-матеріальне забезпечення. Персональні комп’ютери, програмне забезпечення Windows XP, ППЗ GRAN2.

Мета роботи. Отримати навички роботи з педагогічним програмним засобом GRAN2.

Завдання:

4.  Виконати завдання.

5.  Зберегти електронну версію отриманих результати.

6.  Оформити звіт.

Звіт містить такі розділи:

-  Титульний аркуш.

-  Завдання роботи.

-  Письмовий опис дій по виконанню завдань.

-  Отримані результати.

Для роботи у програмі нам знадобляться деякі відомості.

Активні кнопки для швидкого створення об’єктів:

  створити точку

  створити відрізок

  створити промінь

  створити пряму

  створити коло

створити коло за радіусом

  створення середньої точки

  створення точки перетину об’єктів

  створення паралельної прямої

 створення перпендикулярної прямої

  створення ламаної

також це можна зробити за допомогою вкладки «Створити».

Обчислення проводимо за допомогою вкладки «Обчислення».

Для створення динамічного виразу користуємося наступними:

LEN - довжина між двома точками, точкою і прямою, відрізка, кола, дуги, ламаної;

AREA - площа многокутника, кола, дуги, ламаної;

ANGLE - величина кута між трьома точками;

OANGLE - орієнтований кут між трьома точками;

XANGLE – кут нахилу вектора з віссю ОХ;

NORM – відстань від точки до початку координат;

ARG – полярний кут точки;

X – визначити координату точки Х;

Y – визначити координату точки Y.

Практичні завдання

1.  Покажіть, що сума кутів трикутника дорівнює 180°.

2.  З одної точки проведено дві дотичні до кола. Покажіть, що відрізки дотичних рівні.

3.  На стороні АВ трикутника АВС взяли точку D. Покажіть, що відрізок CD менше принаймні однієї з сторін АС або ВС.

4.  Два кола із центрами А і С перетинаються у двох точках E i F. Покажіть, що пряма АС перпендикулярна EF.

5.  Покажіть, що серединні перпендикуляри до двох сторін трикутника перетинаються.

6.  Покажіть, що у будь якому трикутнику всяка сторона менша за півпериметр.

7.  Покажіть, що в прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів (теорема Піфагора)

8.  Покажіть, що центр кола вписаного у трикутник, є точкою перетину його бісектрис.

9.  Знайти значення похідної від функції  в точці .

10.  Знайти значення похідної від функції в точці.

11.  Тіло рухається зі швидкістю, яка змінюється за законом(м/с). Знайдіть шлях, який пройшло тіло за інтервал часу від t=1с до  =3с.

12.  Обчислити роботу, яку треба виконати, щоб викачати воду з ями глибиною 4м., що має квадратний переріз зі стороною 2м. густина  кг/м.

13.  Знайти масу стержня завдовжки 35 см., якщо його лінійна густина змінюється за законом (кг/м).

14.  Знайти кількість електрики, що проходить через поперечний переріз провідника за 10с., якщо сила струму змінюється за законом(А).

15.  Експериментально встановлено, що продуктивність праці робітника наближено виражається формулою , де t - робочий час у годинах. Обчислити обсяг випуску за квартал, вважаючи робочий день восьмигодинним, а кількість робочих днів у кварталі – 62.

16.  Експериментально встановлено, що залежність витрати бензину автомобілем від швидкості на 100 км шляху визначається формулою  , де 30≤v≤110. Визначити середню витрату бензину, якщо швидкість руху 50 – 60 км/год.

Розв’язання вправ