Преобразование Фурье

2.2 Преобразование Фурье

Начнем с комплексного ряда Фурье

Рассмотрим случай L.Тогда сумму можно преобразовать в интеграл следующим образом: определим и =g(y).Так как  возрастает каждый раз на единицу ,то

где .

Таким образом, полученные выше формулы приобретают вид

(4.1)

Величина называется преобразованием Фурье от  и наоборот. Положение множителя  довольно произвольно; часто величины  и  определяют более симметрично:

 (4.2)

Выражения (4.1) или (4.2) можно скомбинировать следующим образом:

(4.3)

Равенство (4.3) удовлетворяется для любой функции  это позволяет сделать интересный вывод об интеграле  как функции . Он равен нулю всюду, кроме точки , а интеграл от него по любому промежутку ,включающему , равен единице, т.е. эта функция имеет бесконечно высокий и бесконечно узкий пик в точке .

Обычно определяют  (Дирака)  следующим образом:

 (4.4)

Из этих уравнений следует, что

 (4.5)

для любой функции , в случае если интервал интегрирования включает точку .

Проделанные выше операции над интегралами Фурье показали, что

 (4.6)

Это интегральное представление функции.

Дельта – функцию можно использовать, чтобы выразить важный интеграл 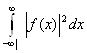 через преобразование Фурье (4.1) от :

(4.7)

Это равенство называется теоремой Парсеваля. Она полезна для понимания физической интерпретации преобразования Фурье для , если известен физический смысл .

Предположим, что  четная функция. Тогда

Заметим теперь, что -- также четная функция. Поэтому

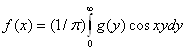(4.9)

Функция и ,определенные теперь только для положительных  и , называются косинус - преобразованиями Фурье по отношению друг к другу.

Рассматривая преобразования Фурье нечетной функции, получаем аналогичные соотношения Фурье между синус - преобразованиями Фурье:

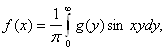
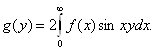 (4.10)

Если нужно, можно симметризовать выражения, поставив множитель  перед каждым интегралом (4.7)-(4.10). [4]