Навигация
Элементы программирования Java 2 используемые в работе
4.2 Элементы программирования Java 2 используемые в работе
При реализации метода аппроксимации оператора эволюции средствами языка программирования Java 2, использовались основные элементы объектно-ориентированного программирования, позволяющие разбить программу на более мелкие структурные части, для дальнейшего совершенствования и настраивания ее под различные физические задачи. Использование технологии AWT позволило создать графический интерфейс, наиболее удобный и понятный различному кругу пользователей. В данной работе использовался модуль JSci.math предназначенный для проведения вычислений в специализированных физических и математических задачах. В качестве среды разработки данного программно приложения использовался Eclipse 3.2.
Анимированный апплет позволяет получить наглядное решение нестационарного уравнения Шредингера в различные моменты времени с различными потенциалами. Также выполненный апплет может быть размещен на Internet-сервере и являться частью jsp-странички, что позволит использовать результаты его вычислений различным пользователям сети Internet, используя Internet-браузер для просмотра данной странички.
Программный код
public class Shreding {
final double K0 = 1.0;
final double C = 0.893;
double i = Math.sqrt(-1);
double hx = (XMax-XMin)/N;
double hp = 2*PMax/N;
double[] x = new double[N+1];{
Wave ob = new Wave();
x = ob.x();}
double[] p = new double[N+1];{
Wave ob = new Wave();
p = ob.p();}
double[] w = new double[N+1];{
Wave ob = new Wave();
w = ob.w();}
double[] rePsyX0 = new double[N+1];{
Wave ob = new Wave();
rePsyX0 = ob.rePsyX0();}
double[] imPsyX0 = new double[N+1];{
Wave ob = new Wave();
imPsyX0 = ob.imPsyX0();}
double[] psyX02 = new double[N+1];{
Wave ob = new Wave();
psyX02 = ob.psyX02();}
double[] rePsyP0 = new double[N+1];{
Wave ob = new Wave();
rePsyP0 = ob.rePsyP0();}
double[] imPsyP0 = new double[N+1];{
Wave ob = new Wave();
imPsyP0 = ob.imPsyP0();}
double[] rePsyPt2 = new double[N+1];{
Wave ob = new Wave();
rePsyPt2 = ob.rePsyPt2();}
double[] imPsyPt2 = new double[N+1];{
Wave ob = new Wave();
imPsyPt2 = ob.imPsyPt2();}
double[] rePsyX1t2 = new double[N+1];{
Wave ob = new Wave();
rePsyX1t2 = ob.rePsyX1t2();}
double[] imPsyX1t2 = new double[N+1];{
Wave ob = new Wave();
imPsyX1t2 = ob.imPsyX1t2();}
double[] rePsyX1t2V = new double[N+1];{
Wave ob = new Wave();
rePsyX1t2V = ob.rePsyX1t2V();}
double[] imPsyX1t2V = new double[N+1];{
Wave ob = new Wave();
imPsyX1t2V = ob.imPsyX1t2V();}
double[] rePsyP1t = new double[N+1];{
Wave ob = new Wave();
rePsyP1t = ob.rePsyP1t();}
double[] imPsyP1t = new double[N+1];{
Wave ob = new Wave();
imPsyP1t = ob.imPsyP1t();}
double[] rePsyP1te = new double[N+1];{
Wave ob = new Wave();
rePsyP1te = ob.rePsyP1te();}
double[] imPsyP1te = new double[N+1];{
Wave ob = new Wave();
imPsyP1te = ob.imPsyP1te();}
double[] rePsyX2t = new double[N+1];{
Wave ob = new Wave();
rePsyX2t = ob.rePsyX2t();}
double[] imPsyX2t = new double[N+1];{
Wave ob = new Wave();
imPsyX2t = ob.imPsyX2t();}
double[] psyX2t = new double[N+1];{
Wave ob = new Wave();
psyX2t = ob.psyX2t();}
/**
*
* Метод осуществляющий вычисление всех моментов времени
*/
public double[][] time(){
double M[][]= new double[N+1][20+15*(NT+1)];
double L[][]= new double[N+1][NT+1];
for (int m = 0; m < N+1; m++){
M[m][0] = x[m];
M[m][1] = p[m];
M[m][2] = w[m];
M[m][3] = rePsyX0[m];
M[m][4] = imPsyX0[m];
M[m][5] = psyX02[m];
}
for (int k = 1; k < NT+1; k++){
for (int j = 0; j < N+1; j++){
M[j][6+15*(k-1)] = rePsyP0[j];
M[j][7+15*(k-1)] = imPsyP0[j];
M[j][8+15*(k-1)] = rePsyPt2[j];
M[j][9+15*(k-1)] = imPsyPt2[j];
}
for (int m = 0; m < N+1; m++){
M[m][10+15*(k-1)] = rePsyX1t2[m];
M[m][11+15*(k-1)] = imPsyX1t2[m];
M[m][12+15*(k-1)] = rePsyX1t2V[m];
M[m][13+15*(k-1)] = imPsyX1t2V[m];
}
for (int j = 0; j < N+1; j++){
M[j][14+15*(k-1)] = rePsyP1t[j];
M[j][15+15*(k-1)] = imPsyP1t[j];
M[j][16+15*(k-1)] = rePsyP1te[j];
M[j][17+15*(k-1)] = imPsyP1te[j];
}
for (int m = 0; m < N+1; m++){
M[m][18+15*(k-1)] = rePsyX2t[m];
M[m][19+15*(k-1)] = imPsyX2t[m];
M[m][20+15*(k-1)] = psyX2t[m];
rePsyX0 = rePsyX2t;
imPsyX0 = imPsyX2t;
L[m][k] = M[m][20+15*(k-1)];
}
}return L;
}
}
class Wave{
final double K0 = 1.0;
final double C = 0.893;
double i = Math.sqrt(-1);
double hx = (XMax-XMin)/N;
double hp = 2*PMax/N;
/**
*
* Вычисление координат x
*/
double[] x(){
double X[] = new double[N+1];
for (int j = 0; j < N+1; j++){
X[j] = XMin+j*hx;
}return X;
}
double[] x = new double[N+1];{
x = x();}
**
*
* Вычисление импульсов p
*/
double[] p(){
double P[] = new double[N+1];
for (int j = 0; j < N+1; j++){
P[j] = -1*PMax + j*hp;
}return P;
}
double[] p = new double[N+1];{
p = p();}
/**
*
* Построение потенциального барьера
*/
double[] w(double a, double b, double VMax){
double W[]= new double[N+1];
for (int j = 0; j < N+1; j++){
double V = 0;
if (x[j]>a && x[j]<b){
V = VMax;
}W[j] = V;
}return W;
}
double[] w = new double[N+1];{
w = w();}
/**
*
* Действительная часть функци Psy в начальный момент времени
*/
double[] rePsyX0(){
double RePsyX0[]= new double[N+1];
for (int j = 0; j < N+1; j++){
RePsyX0[j] = C*Math.exp(-x[j]*x[j])*Math.cos(K0*x[j]);
}return RePsyX0;
}
double[] rePsyX0 = new double[N+1];{
rePsyX0 = rePsyX0();}
/**
*
* Мнимая часть функци Psy в начальный момент времени
*/
double[] imPsyX0(){
double ImPsyX0[]= new double[N+1];
for (int j = 0; j < N+1; j++){
ImPsyX0[j] = C*Math.exp(-x[j]*x[j])*Math.sin(K0*x[j]);
}return ImPsyX0;
}
double[] imPsyX0 = new double[N+1];{
imPsyX0 = imPsyX0();}
/**
*
* Вероятность в нвчальный момент времени
*/
double[] psyX02(){
double[] L = new double[N+1];
double[] K = new double[N+1];
double[] PsyX02 = new double[N+1];
L = rePsyX0;
K = imPsyX0;
for (int j = 0; j < N+1; j++){
PsyX02[j] = L[j]*L[j] + K[j]*K[j];
}return PsyX02;
}
double[] psyX02 = new double[N+1];{
psyX02 = psyX02();}
/**
*
* Первое преобразование Фурье и вычисление действительной части функции Psy
*/
double[] rePsyP0(){
double RePsyP0[]= new double[N+1];
for (int j=0; j<N+1; j++){
double S = 0;
for (int s=0; s<N+1; s++){
S += rePsyX0[s]*Math.cos(p[j]*x[s]) + imPsyX0[s]*Math.sin(p[j]*x[s]);
}
RePsyP0[j] = hx*S/Math.sqrt(2*Math.PI);}
//rePsyX0 = rePsyX2t;
//imPsyX0 = imPsyX2t;
return RePsyP0;
}
double[] rePsyP0 = new double[N+1];{
rePsyP0 = rePsyP0();}
/**
*
* Первое преобразование Фурье и вычисление мнимой части функции Psy
*/
double[] imPsyP0(){
double ImPsyP0[]= new double[N+1];
for (int j=0; j<N+1; j++){
double S = 0;
for (int s=0; s<N+1; s++){
S += imPsyX0[s]*Math.cos(p[j]*x[s]) - rePsyX0[s]*Math.sin(p[j]*x[s]);
}
ImPsyP0[j] = hx*S/Math.sqrt(2*Math.PI);}
//rePsyX0 = rePsyX2t;
//imPsyX0 = imPsyX2t;
return ImPsyP0;
}
double[] imPsyP0 = new double[N+1];{
imPsyP0 = imPsyP0();}
/**
*
* Произведение действительной части функции Psy и первой составляющей оператора расщепления
*/
double[] rePsyPt2(){
double RePsyPt2[]= new double[N+1];
for (int j=0; j<N+1; j++){
RePsyPt2[j] = rePsyP0[j]*Math.cos(p[j]*p[j]*DT/2) + imPsyP0[j]*Math.sin(p[j]*p[j]*DT/2);
}return RePsyPt2;
}
double[] rePsyPt2 = new double[N+1];{
rePsyPt2 = rePsyPt2();}
/**
*
* Произведение мнимой части функции Psy и первой составляющей оператора расщепления
*/
double[] imPsyPt2(){
double ImPsyPt2[]= new double[N+1];
for (int j=0; j<N+1; j++){
ImPsyPt2[j] = imPsyP0[j]*Math.cos(p[j]*p[j]*DT/2) - rePsyP0[j]*Math.sin(p[j]*p[j]*DT/2)*0;
}return ImPsyPt2;
}
double[] imPsyPt2 = new double[N+1];{
imPsyPt2 = imPsyPt2();}
/**
*
* Второе преобразование Фурье и вычисление действительной части функции Psy
*/
double[] rePsyX1t2(){
double RePsyX1t2[]= new double[N+1];
for (int j=0; j<N+1; j++){
double S = 0;
for (int s=0; s<N+1; s++){
S += rePsyPt2[s]*Math.cos(p[s]*x[j]) - imPsyPt2[s]*Math.sin(p[s]*x[j]);
}
RePsyX1t2[j] = hp*S/Math.sqrt(2*Math.PI);
}return RePsyX1t2;
}
double[] rePsyX1t2 = new double[N+1];{
rePsyX1t2 = rePsyX1t2();}
/**
*
* Второе преобразование Фурье и вычисление мнимой части функции Psy
*/
double[] imPsyX1t2(){
double ImPsyX1t2[]= new double[N+1];
for (int j=0; j<N+1; j++){
double S = 0;
for (int s=0; s<N+1; s++){
S += imPsyPt2[s]*Math.cos(p[s]*x[j]) + rePsyPt2[s]*Math.sin(p[s]*x[j]);
}
ImPsyX1t2[j] = hp*S/Math.sqrt(2*Math.PI);
}return ImPsyX1t2;
}
double[] imPsyX1t2 = new double[N+1];{
imPsyX1t2 = imPsyX1t2();}
/**
*
* Произведение действительной части функции Psy и второй составляющей оператора расщепления
*/
double[] rePsyX1t2V(){
double RePsyX1t2V[]= new double[N+1];
for (int j=0; j<N+1; j++){
RePsyX1t2V[j] = rePsyX1t2[j]*Math.cos(w[j]*DT) + imPsyX1t2[j]*Math.sin(w[j]*DT);
}return RePsyX1t2V;
}
double[] rePsyX1t2V = new double[N+1];{
rePsyX1t2V = rePsyX1t2V();}
/**
*
* Произведение мнимой части функции Psy и второй составляющей оператора расщепления
*/
double[] imPsyX1t2V(){
double ImPsyX1t2V[]= new double[N+1];
for (int j=0; j<N+1; j++){
ImPsyX1t2V[j] = imPsyX1t2[j]*Math.cos(w[j]*DT) - rePsyX1t2[j]*Math.sin(w[j]*DT);
}return ImPsyX1t2V;
}
double[] imPsyX1t2V = new double[N+1];{
imPsyX1t2V = imPsyX1t2V();}
/**
*
* Третье преобразование Фурье и вычисление действительной части функции Psy
*/
double[] rePsyP1t(){
double RePsyP1t[]= new double[N+1];
for (int j=0; j<N+1; j++){
double S = 0;
for (int s=0; s<N+1; s++){
S += rePsyX1t2V[s]*Math.cos(p[j]*x[s]) + imPsyX1t2V[s]*Math.sin(p[j]*x[s]);
}
RePsyP1t[j] = hx*S/Math.sqrt(2*Math.PI);
}return RePsyP1t;
}
double[] rePsyP1t = new double[N+1];{
rePsyP1t = rePsyP1t();}
/**
*
* Третье преобразование Фурье и вычисление мнимой части функции Psy
*/
double[] imPsyP1t(){
double ImPsyP1t[]= new double[N+1];
for (int j=0; j<N+1; j++){
double S = 0;
for (int s=0; s<N+1; s++){
S += imPsyX1t2V[s]*Math.cos(p[j]*x[s]) - rePsyX1t2V[s]*Math.sin(p[j]*x[s]);
}
ImPsyP1t[j] = hx*S/Math.sqrt(2*Math.PI);
}return ImPsyP1t;
}
double[] imPsyP1t = new double[N+1];{
imPsyP1t = imPsyP1t();}
/**
*
* Произведение действительной части функции Psy и третьей составляющей оператора расщепления
*/
double[] rePsyP1te(){
double RePsyP1te[]= new double[N+1];
for (int j=0; j<N+1; j++){
RePsyP1te[j] = rePsyP1t[j]*Math.cos(p[j]*p[j]*DT/2) + imPsyP1t[j]*Math.sin(p[j]*p[j]*DT/2);
}return RePsyP1te;
}
double[] rePsyP1te = new double[N+1];{
rePsyP1te = rePsyP1te();}
/**
*
* Произведение мнимой части функции Psy и третьей составляющей оператора расщепления
*/
double[] imPsyP1te(){
double ImPsyP1te[]= new double[N+1];
for (int j=0; j<N+1; j++){
ImPsyP1te[j] = imPsyP1t[j]*Math.cos(p[j]*p[j]*DT/2) - rePsyP1t[j]*Math.sin(p[j]*p[j]*DT/2);
}return ImPsyP1te;
}
double[] imPsyP1te = new double[N+1];{
imPsyP1te = imPsyP1te();}
/**
*
* Четвертое преобразование Фурье и вычисление действительной части функции Psy
*/
double[] rePsyX2t(){
double RePsyX2t[]= new double[N+1];
for (int j=0; j<N+1; j++){
double S = 0;
for (int s=0; s<N+1; s++){
S += rePsyP1te[s]*Math.cos(p[s]*x[j]) - imPsyP1te[s]*Math.sin(p[s]*x[j]);
}
RePsyX2t[j] = hp*S/Math.sqrt(2*Math.PI);
}return RePsyX2t;
}
double[] rePsyX2t = new double[N+1];{
rePsyX2t = rePsyX2t();}
/**
*
* Четвертое преобразование Фурье и вычисление мнимой части функции Psy
*/
double[] imPsyX2t(){
double ImPsyX2t[]= new double[N+1];
for (int j=0; j<N+1; j++){
double S = 0;
for (int s=0; s<N+1; s++){
S += imPsyP1te[s]*Math.cos(p[s]*x[j]) + rePsyP1te[s]*Math.sin(p[s]*x[j]);
}
ImPsyX2t[j] = hp*S/Math.sqrt(2*Math.PI);
}return ImPsyX2t;
}
double[] imPsyX2t = new double[N+1];{
imPsyX2t = imPsyX2t();}
/**
*
* Вычисление вероятности в момент DT
*/
double[] psyX2t(){
double[] L = new double[N+1];
double[] K = new double[N+1];
double[] PsyX2t = new double[N+1];
L = rePsyX2t;
K = imPsyX2t;
for (int j = 0; j < N+1; j++){
PsyX2t[j] = L[j]*L[j] + K[j]*K[j];
}return PsyX2t;
}
}
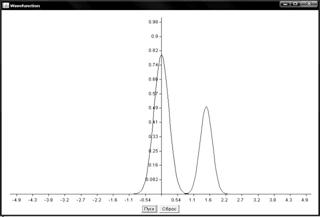
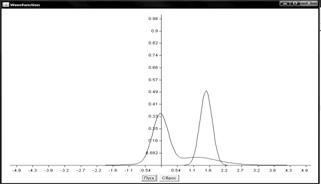
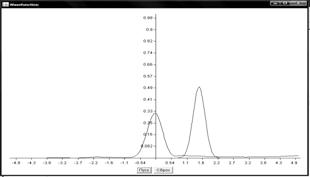
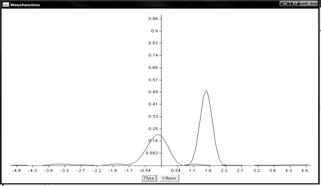
Графики поведения волновых функций
Прямоугольный потенциальный барьер
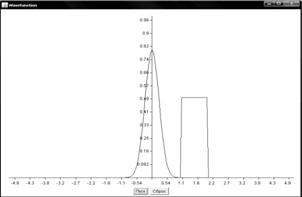
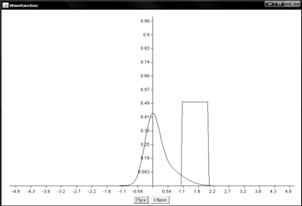
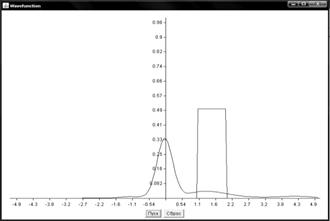
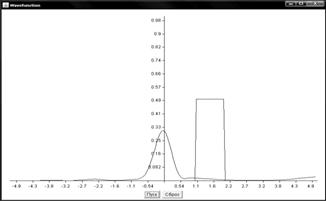
Барьер гауссова функция
Заключение
Численное решение нестационарного уравнения Шредингера имеет важное значение для компьютерного исследования квантовых систем. В данной работе рассмотрены два метода численного решения одномерного нестационарного уравнения Шредингера: метод конечных разностей и метод аппроксимации оператора эволюции. По результатам вычислений построены графики поведения волновой функции в зависимости от времени для ступенчатого потенциала.
Полученные значения полностью соответствуют теоретическим данным для квантовомеханической задачи со ступенчатым потенциалом и наглядно отражают процессы отражения и прохождения частицы через потенциальный барьер. Также рассмотренные численные методы могут использоваться для расчета других видов волновых функций и потенциалов.
Список использованных источников
1. А.С. Давыдов. Квантовая механика//М.,: "Наука", 1973г., 704 с
2. З. Флюгге. Задачи по квантовой механике//М.: "Мир", Т.1, 1974г., 343 с
3. Е.А. Волкова, А.М. Попов, А.Т. Рахимов, "Квантовая механика на персональном компьютере"//Москва.: "УРСС", 1995.
4. Дж. Мэтьюз, Р. Уокер "Математические методы физики".
4. С.В. Поршнев Моделирование квантовых систем //www.exponenta.ru
6. П.Ноутон, Г.Шилдт Java 2 Наиболее полное руководство//С-Петербург: "БХВ-Петербург" 2007.
0 комментариев