Методы численного решения стационарного уравнения Шредингера

3. Методы численного решения стационарного уравнения Шредингера

3.1 Метод Нумерова

Рассмотрим решения одномерного стационарного уравнения Шредингера (3.1) частицы, движущейся в одномерном потенциале U(x).

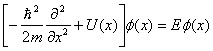(3.1)

Будем при этом полагать, что его форма имеет потенциала, представленного на рис.1: в точках x_min, x_max потенциал становится бесконечно большим. Это означает, что в точках x_min, x_max расположены вертикальные стенки, а между ними находится яма конечной глубины.

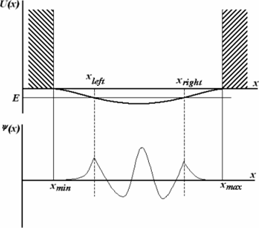
Рисунок 1.

Для удобства дальнейшего решения запишем уравнение Шредингера (3.1) в виде:

(3.2)

Где

(3.3)

С математической точки зрения задача состоит в отыскании собственных функций оператора, отвечающим граничным условиям

(3.4)

и соответствующих собственных значений энергии E.

Так как при  и  при , , то можно ожидать, что собственному решению данной задачи соответствует собственная функция, осциллирующая в классически разрешенной области движения  и экспоненциально затухающим в запрещенных областях, где  ,, при ,  . Так как все состояния частицы в потенциальной яме оказываются связанными (т.е. локализованными в конечной области пространства), спектр энергий является дискретным. Частица, находящаяся в потенциальной яме конечных размеров  при ,  при , имеет дискретный спектр при  и непрерывный спектр при .

Традиционно для решении задачи о нахождении собственных значений уравнения Шредингера используется метод пристрелки. Идея метода пристрелки состоит в следующем. Допустим, в качестве искомого значения ищется одно из связанных состояний, поэтому в качестве пробного начального значения энергии выбираем отрицательное собственное значение. Проинтегрируем уравнение Шредингера каким-либо известным численным методом на интервале . По ходу интегрирования от  в сторону больших значений  сначала вычисляется решение  , экспоненциально нарастающее в пределах классически запрещенной области. После перехода через точку поворота , ограничивающую слева область движения разрешенную классической механикой, решение уравнения становится осциллирующим. Если продолжить интегрирование далее за правую точку поворота , то решение становится численно неустойчивым. Это обусловлено тем, что даже при точном выборе собственного значения, для которого выполняется условие , решение в области  всегда может содержать некоторую примесь экспоненциально растущего решения, не имеющего физического содержания. Отмеченное обстоятельство является общим правилом: интегрирование по направлению вовнутрь области, запрещенной классической механикой, будет неточным. Следовательно, для каждого значения энергии более разумно вычислить еще одно решение , интегрируя уравнение (3.1) от  в сторону уменьшения . Критерием совпадения данного значения энергии является совпадение значений функций  и  в некоторой промежуточной точке . Обычно в качестве данной точки выбирают левую точку поворота . Так как функции , являются решениями однородного уравнения (3.1), их всегда можно нормировать так, чтобы в точке  выполнялось условие . Помимо совпадения значений функций в точке  для обеспечения гладкости сшивки решений потребуем совпадения значений их производных

(3.5)

Используя в (17) простейшие левую и правую конечно-разностные аппроксимации производных функций ,  в точке , находим эквивалентное условие гладкости сшивки решений:

(3.6)

Число  является масштабирующим множителем, который выбирается из условия  Если точки поворота отсутствуют, т.е. E>0, то в качестве  можно выбрать любую точку отрезка . Для потенциалов, имеющих более двух точек поворота и, соответственно, три или более однородных решений, общее решение получается сшивкой отдельных кусков. В описанном ниже документе, для интегрирования дифференциального уравнения второго порядка мы используем метод Нумерова. Для получения вычислительной схемы аппроксимируем вторую производную трехточечной разностной формулой:

(3.7)

Из уравнения (3.1) имеем

(3.8)

Подставив (3.7) в (3.8) и перегруппировав члены, получаем

(3.9)

Разрешив (3.9) относительно  или , найдем рекуррентные формулы для интегрирования уравнения (3.1) вперед или назад по  c локальной погрешностью . Отметим, что погрешность данного метода оказывается на порядок выше, чем погрешность метода Рунге-Кутта четвертого порядка. Кроме того данный алгоритм более эффективен, потому что значение функции  вычисляются только в узлах сетки. Для нахождения численного решения оказывается удобным провести обезразмеривание уравнения (3.1), используя в качестве единиц измерения расстояния  - ширину потенциальной ямы, в качестве единиц измерения энергии - модуль минимального значения потенциала . В выбранных единицах измерения уравнение (3.1) имеет вид

(3.10)

где

   (3.11)

Таким образом, вычислительный алгоритм для нахождения собственных функций и собственных значений уравнения Шредингера реализуется следующей последовательностью действий:

1. Задать выражение, описывающее безразмерный потенциал .

2. Задать значение .