Навигация
Предельные теоремы. Характеристические функции
6903
знака
1
таблица
0
изображений
Предельные теоремы. Характеристические функции
1. Теорема Чебышева
Теория вероятностей изучает закономерности массовых случайных явлений. Если явление носит единичный характер, то теория вероятностей не может предсказать исход события.
Иное дело, когда явление – массовое. Закономерности проявляются именно при большом числе случайных событий, происходящих в однородных условиях.
При большом числе испытаний характеристики случайных событий и случайных величин практически мало изменяются, т.е. становятся неслучайными. Это обстоятельство позволяет использовать результаты наблюдений над случайными явлениями для предсказания результатов будущих испытаний.
В дальнейшем мы ознакомимся с двумя типами предельных теорем: законом больших чисел и центральной предельной теоремой. Закон больших чисел играет очень важную роль в практическом применении теории вероятностей к явлениям природы и техническим процессам, связанных с массовым производством.
Для доказательства этих теорем воспользуемся неравенством Чебышева.
Пусть mxи Dx – математическое ожидание и дисперсия случайной величины Х.
Тогда неравенство Чебышева гласит: вероятность того, что отклонение случайной величины от ее математического ожидания будет по абсолютной величине не меньше любого положительного числа 
, ограничена величиной 
, т.е.
Доказательство. Пусть Х – непрерывная случайная величина с плотностью распределения вероятностей f(x). По определению
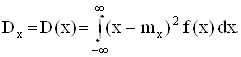(1)
Выделим на числовой оси интервал АВ, состоящий из точек 
А В
х
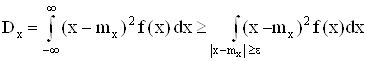
Так как теперь 
, то
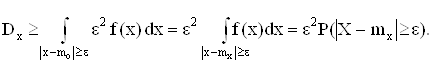
Отсюда непосредственно и вытекает неравенство Чебышева.
Если Х – дискретная случайная величина, то доказательство неравенства Чебышева проводится по проделанной выше схеме с той лишь разницей, что вместо интеграла нужно записать сумму.
Так как
,
то неравенство Чебышева можно записать в другом виде
Если взять 
, то получим, что неравенство Чебышева дает оценку
,
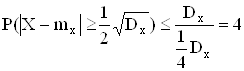что заведомо выполняется, т.к. вероятность 
С другой стороны, если взять 
, то
,
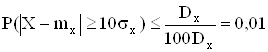т.е. дает неплохую оценку. Таким образом, мы видим, что неравенство Чебышева полезно лишь относительно (относительно sх) больших 
Теорема Чебышева. При неограниченном увеличении числа независимых испытаний среднее арифметическое наблюдаемых значений случайной величины, имеющих конечную дисперсию, сходится по вероятности к ее математическому ожиданию.
Определение. Случайные величины 
сходятся по вероятности к величине а, если для 
, начиная с которого выполняется неравенство 
или, по другому, если для любого малого 
Итак, нужно доказать, что для любого малого
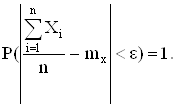
Доказательство. Введем случайную величину
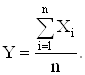
Найдем числовые характеристики случайной величины Y, пользуясь их свойствами:
Теперь применим неравенство Чебышева к случайной величине Y:
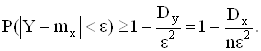
Так как по условию Dx ограничена, то
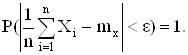
Прежде чем сформулировать центральную предельную теорему введем характеристические функции.
Похожие работы
... и докажу теорему Ляпунова только в частном случае, т.е. для последовательности независимых и одинаково распределенных случайных величин. Центральная предельная теорема. Пусть — независимые и одинаково распределенные случайные величины с конечной и ненулевой дисперсией: . Обозначим через сумму первых случайных величин: . Тогда последовательность случайных величин слабо сходится к ...
... функциям, не выводят нас за пределы этого класса функций. Следующая теорема устанавливает сходный результат относительно уже не арифметической операции – предельного перехода. Теорема 2. Пусть на множестве Е задана последовательность измеримых функций f1(x), f2(x), … Если в каждой точке хЕ существует (конечный или бесконечный) предел F(x)=fn(x), то функция F(х) измерима. Д о к а з а т е л ь с ...
... проверить знания студента из первой части курса, которая излагается в первых четырёх модулях. Во вторых вопросах билета проверяются знания классической предельной проблемы теории вероятностей и математической статистики, которые излагаются в следующих пяти модулях. 1. Вероятностная модель с не более чем счётным числом элементарных исходов. Пример: испытания с равновозможными исходами. 2. ...
... математической модели (распределения сумм пуассоновского числа нормально распределенных случайных величин). ЗАКЛЮЧЕНИЕ В данной курсовой работе рассмотрены основные методы прогнозирования экономической среды с учетом фактора старения информации на примере рыночного механизма спрос-предложение. Проанализировав полученную информацию, можно сделать выводы о том, что для различных наук, отраслей ...
0 комментариев