Навигация
Многофакторный корреляционно-регрессионный анализ
55804
знака
11
таблиц
2
изображения
2. Многофакторный корреляционно-регрессионный анализ
На основании вышеперечисленных показателей составить матрицу и по программе STRAZ решить задачу множественной корреляции.
По совокупности хозяйств построить корреляционное уравнение связи урожайности зерновых и зернобобовых культур с включением трех-четырех факторов.
Анализ корреляционной модели начинается с определения тесноты связи, ее характеризует коэффициент корреляции (R). Он может изменяться от 0 до 1, что свидетельствует об отсутствии связи или о слабой, средней и тесной связи.
Квадрат коэффициента множественной корреляции называется коэффициентом множественной детерминации. Он характеризует величину вариации результативного признака, которая объединяется факторами, входящими в модель. В матрице этот коэффициент равен, например, 0,4321, для анализа необходимо перевести его в проценты, что составит 43%. Это значит, что 43% вариации результативного признака обусловлено влиянием факторов, включенных в модель, или на 43% выбранные факторы влияют на величину У (урожайность).
Коэффициенты отдельного определения или частные коэффициенты детерминации отражают «чистый вклад» каждого фактора в воспроизведенную вариацию результативного признака. Наибольшую тесноту связи с результативным признаком имеет тот фактор, коэффициент при котором наибольший (например, если коэффициент при Х4 равен 0,5, это значит, что качество земли на 50% влияет на уровень урожайности).
Коэффициенты чистой регрессии показывают, на сколько ц с 1 га увеличится урожайность при изменении фактора на 1 единицу измерения. Например, если коэффициент при Х3 равен 0,3, это значит, что при увеличении энергообеспеченности на 1 л.с., урожайность увеличится на 0,3 ц с 1 га.
Каждый из 
-коэффициентов показывает, на сколько средних квадратических отклонений изменится в среднем урожайность, если соответствующий фактор изменится на одно среднее квадратическое отклонение. Сопоставляя -коэффициенты между собой, можно определить, какой фактор оказывает наиболее сильное влияние на варьирование результативного признака.
Каждый из коэффициентов эластичности показывает, на сколько процентов в среднем изменится урожайность, если соответствующий фактор изменится на 1%.
Знак + или - говорит о прямой или обратной связи между урожайностью и фактором.
Построить уравнение регрессии:
у=а0 + a1x1 + а2х2 + ... +anxn, где: (1)
а0 — свободный член, экономического значения не имеет;
a1, a2, an- коэффициенты чистой регрессии;
x1, х2, xn - значения соответствующих факторов.
у=153,4+3,7*9594+0,04*9382+(-4,3)*5848+(-0,01)*5020+(-0,01)*4700+5,2*4090+0,1*3915+2*3735+0,2*3700
На основании полученного уравнения регрессии рассчитать прогнозируемый уровень урожайности для хозяйств зоны. Для этого в уравнение вместо X подставить самые высокие их значения из матрицы и вместо а - соответствующие значения коэффициентов.
Полученный результат означает, что в хозяйствах, где урожайность выше среднего уровня, в будущем возможно достичь прогнозируемого уровня урожайности и при условии достижения каждым хозяйством максимальных значений факторов (или минимальных, если коэффициент со знаком «минус»). [10, с.109]
Произведем расчет множественной регрессии в MS Excel. (Приложение В)
3. Вычисление параметров парной регрессии и корреляции
Рассмотрим взаимосвязь между фактической посевной площадью (Y) и наличием тракторов (Х). Исходные данные. (Приложение А)
Все расчеты сведены в таблицу. (Приложение Б)
Линейная модель парной регрессии и корреляции
Рассмотрим простейшую модель парной регрессии – линейную регрессию. Линейная регрессия находит широкое применение в эконометрике ввиду четкой эконометрической интерпретации ее параметров.
Линейная регрессия сводится к нахождению уравнения вида
, (2)
где а – свободный член уравнения регрессии, y – среднее значение результативного признака, b – коэффициент регрессии, характеризующий силу связи между вариацией факторного признака и и вариацией результативного признака.
Составим систему линейных уравнений для оценки параметров а и b:
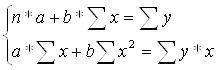
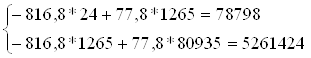(3)
Решая систему уравнений (3), найдем искомые оценки параметров а и b.
Получаем уравнение парной регрессии
Похожие работы
... несколько уравнений, а в каждом уравнении - несколько переменных. Задача оценивания параметров такой разветвленной модели решается с помощью сложных и причудливых методов. Однако все они имеют одну и ту же теоретическую основу. Поэтому для получения начального представления о содержании эконометрических методов мы ограничимся в последующих параграфах рассмотрением простой линейной регрессии. ...
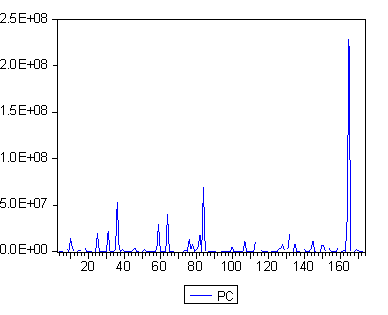
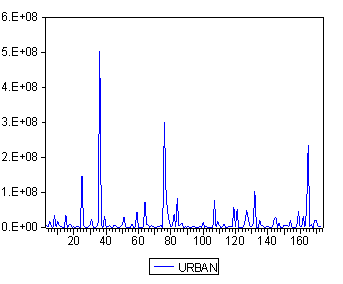
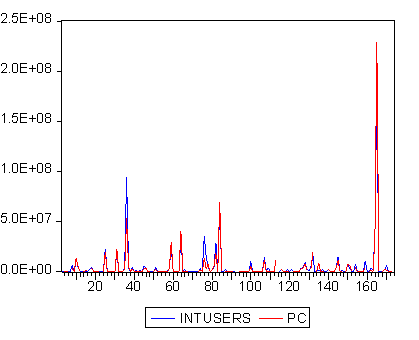
... 964982 0.426228 PC 0.557379 0.331656 0.438161 0.964982 1.000000 0.211864 RURAL 0.873801 -0.068260 -0.060708 0.426228 0.211864 1.000000 Видим, что на численность пользователей Интернет огромное влияние оказывает число компьютеров в стране. Кроме того, немаловажное значение имеет численность урбанизированного населения. Численность городского населения сильно зависит от ...
... и боятся бедности и как следствие воспитывают своих детей в такой же привычке к труду и благосостоянию, а удача доставляет удовлетворение их родительским чувствам и самолюбию. Принадлежит первое в истории экономической мысли достаточно глубокое теоретическое обоснование положений о капитале. Считал, “что деньги сами по себе представляют собой бесплодное богатство, которое ничего не производит”. ...
... направлений. Выбор направлений в каждом случае будет обусловлен задачами анализа, его масштабом и сроками, которые должен определять заказчик. 2. Методы маркетинговых исследований в регионе Существуют различные классификации методов экономического анализа. Первый уровень классификации выделяет неформализованные и формализованные методы анализа. Первые основаны на описании аналитических ...
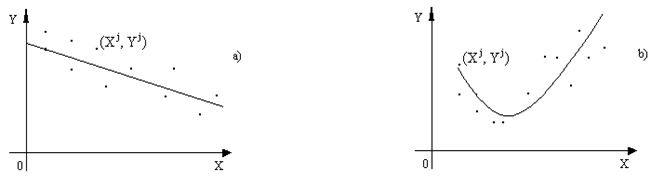
0 комментариев