Перший алгоритм Гомори

3. Перший алгоритм Гомори

Випливаючи загальній схемі методів відсікання, вирішимо (£, C) – задачу (11, 12, 14), що відповідає (£^ц, C) – задачі (11–14). Нехай x(£, C) – її оптимальне рішення. Проаналізуємо координати x(£, C) на цілочисленність. Якщо всі координати вектора x(£, C) цілі, то x(£, C) = x(£^ц, C). Якщо хоча б одна координата, нехай x_i, буде нецілої, надійдемо в такий спосіб.

Позначимо через N сукупність небазисних змінних і на підставі останньої симплексної таблиці запишемо розкладання x_i по небазисним змінним x_i, jÎN

(16)

Тому що x_i – неціла величина, позначимо найближче ціле число, що не перевершує x_i, через [x_i] і визначимо дробову частину: {x_i}= x_i - [x_i]. Очевидно, (x_i)>0.

Покажемо, що по i-і рядку симплексної таблиці (?, C) - задачі (у якій коштує неціла координата рішення) можна визначити додаткове лінійне обмеження, що володіє властивостями правильності.

Теорема. Нехай - припустиме рішення (£^ц, C) – задачі, тоді співвідношення

, (17)

, - ціле,

визначають правильне відсікання.

Доказ.

Запишемо вираження (16) у вигляді:

Використовуючи для цього вираження формулу (17), одержимо:

або

На підставі припущень теореми про допустимість рішення

(£^ц, C) – задачі x_i – ціле. Величини [x_io], - цілі по визначенню, отже, z_i – теж ціле.

Отже, z_i певне формулою (17), ціле. Доведемо що . Доказ будемо вести від противного. Нехай .-

Це значить, що . По визначенню дробової частини . За умовою теореми x – припустиме рішення (£^ц, C) – задачі, тому . Отже,

Тоді повинне виконуватися:

Отже, із припущення заперечності z_i, відразу ж одержуємо  тобто z_i – неціле. Оскільки раніше було показано, що z_i, певне формулою (17), є цілим, те тим самим ми прийшли до протиріччя. Отже, припущення, що z_i < 0, невірне. Теорема доведена.

Наслідок. Будь-яке оптимальне рішення x(£, C) (£, C) – задачі, що не є припустимим рішенням (£^ц, C) – задачі, не задовольняє умові правильного відсікання (17).

Доказ. Нехай х (£, C) – оптимальне рішення (£, C) – задачі, x_i0 – дробове.

Покажемо, що х (£, C) не задовольняє умові відсікання. Оскільки план оптимальний, всі небазисні змінні x_i, для jÎN дорівнюють нулю. Тому . З огляду на це, підставимо x_io у формулу (17):

z_i(x (£, C))= – {x_i0}+0<0,

що суперечить умові незаперечності z_i. Наслідок доведений.

Очевидно, що кількість додаткових обмежень буде наростати в міру рішення допоміжних (£, C) – задач, оптимальні плани яких будуть містити нецілі координати, тобто виникає проблема розмірності.

Р. Гомори запропонував прийом, що дозволяє обмежити розміри розглянутих симплексних таблиць допоміжних задач величиною (n+2) (k+1), де n – кількість змінних (£, C) – задачі, k – число небазисних змінних її. Цей прийом ґрунтується на тім, що нас цікавить додаткове обмеження лише як спосіб відсікання нецілочисленного оптимального рішення допоміжної задачі, отриманої на даному кроці, і переходу до наступної задачі.

Послідовність (£, C) – задач позначимо індексом k=0,1,…,відповідному номеру ітерації в послідовному наближенні до рішення вихідної (£^ц, C) – задачі, і позначимо (£_k, C). При цьому (£₀, C) – задача відповідає (£, C) – задачі (задачі без вимоги цілочисленності).

Змінну z_i, що визначається додатковим лінійним обмеженням (7) і будується по деякої нецілочисленної координаті оптимального рішення (£_k, C) – задачі (k =0, 1, 2,…)позначимо x_n+k+l.

Щоб розмірність послідовності (£_k, C) – задач не зростала, викреслимо із симплекс-таблиці змінну, по якій побудоване додаткове лінійне обмеження.

Після зроблених зауважень перейдемо безпосередньо до викладу обчислювальної схеми.

1. Вирішимо (£_k, C) – задачу (спочатку k = 0) методом послідовного поліпшення плану.

Нехай у базис оптимального рішення ввійшли вектори A_s1,…,A_sm... Параметри останньої симплексної таблиці позначимо через x_ij:

.

Якщо, всі базисні тридцятилітні  оптимального рішення x(£_k, C) (£_k, C) – задачі цілі, то x(£_k, C) = x(£^ц, C). Якщо деяка координата x_io оптимального рішення x(£_k, C) неціла, то перейдемо до п. 2.

2. Якщо серед сукупності координат оптимального рішення x(£_k, C) є єдина неціла координата, то додаткове лінійне обмеження (17) будується по цій координаті. Якщо нецілих координат в x(£_k, C) більше однієї, то виберемо координату з найменшим номером. Нехай нею виявилася x_i0. Складемо додаткове лінійне обмеження

(18)

(19)

3. Додамо умови (18, 19) до умов (£_k, C) – задачі. Одержимо нову (£_{k+1, C) – задачу. Тому що оптимальне рішення x(£k}, C) (£_k, C) – задачі визначало одну з вершин багатогранника умов, то воно може бути обране в якості первісного опорного рішення для знову отриманої задачі. А це означає, що останню симплексну таблицю (£_k, C) – задачі можна взяти в якості вихідної для (£_{k+1, C) – задачі, доповнивши її умовою (18).}

Отже, симплексна таблиця для (£_{k+1, C) – задачі виходить із останньої симплексної таблиці для (£k}, C) – задачі шляхом облямівки (i+1) – й рядком з елементами:

де  – небазисні змінні (£_k, C) задачі.

Одержимо нову задачу, змінними якої є . Умови цієї задачі дозволені відносно x_sl,…,x_smзмінних і нова змінної x_n+k+1, а лінійна форма виражена через небазисні змінні (£_k, C) – задачі. Тому що ми займаємося максимізацією F(x) і рішення х* для (£_k, C) – задачі оптимально, те всі D_i > 0. Тому процес переходу до нового рішення (£_{k+1, C) – задачі не може бути здійснений по методу уточнення плану. У той же час  і тому вектор А0} симплексної таблиці не є опорним рішенням для (£_{k+1, C) – задачі, тому що рішенням називається вектор, всі координати якого ненегативні й задовольняють умові приналежності області £k+l}. Тому назвемо отриманий вектор  псевдо рішенням задачі (£_{k+1, C) і перейдемо до подальшого перетворення симплекса-таблиці.}

Позначимо через k номер псевдо рішення (£_k, C) – задачі; тоді напрямним рядком є i+k+ 1-я рядок, k =0, 1, 2,…... Тому на кожному етапі перетворення таблиці вектор A_i+k+i буде виводитися з таблиці. Можна довести, що через кінцеве число кроків або буде знайдене цілочисленне рішення, або буде виявлена її нерозв'язність, а тим самим нерозв'язність (£^ц, C) – задачі.

Якщо рішення (£_k, C) – задачі завершується побудовою оптимального цілочисленного рішення x*, те m, перших його компонентів визначають рішення цілочисленної задачі; якщо серед координат х* є дробові, те один із дробових компонентів (раніше певним правилом) породжує додаткове обмеження й процес рішення повинен бути продовжений з новим рядком, що облямовує. Рядок, використовуваний раніше для облямівки, викреслюється й більше для побудови розширених задач не відновлюється.

Процедуру рішення (£_k, C) – задачі (k=0, 1,…)і аналізу отриманого рішення назвемо великою ітерацією. Номер великої ітерації збігається з номером розв'язуваної (£_k, C) – задачі.

Результатом великої ітерації є перехід до нового (£_{k+1, C) – задачі або закінчення рішення задачі.}

Уведемо: 1) осередок i, у якій будемо запам'ятовувати номер рядка, на підставі якої будується чергове додаткове лінійне обмеження, 2) лічильник r, що відповідає номеру проведеної великої ітерації. Позначимо x*(£^r, C) оптимальне рішення (£^r, C) – задачі. Помітимо, що позначення (£^r, C) – задача, еквівалентне (£_r, C), уведено в блок-схемі для зручності запису.

При деяких умовах вдається довести теорему про кінцівку першого алгоритму Гомори, що ми приведемо без доказу.

Теорема. Нехай множина оптимальних планів задачі (£₀, C) обмежено й виконуються наступні умови:

1) с_i – цілі коефіцієнти цільової функції F(x) (i =1,2,…,n),рядок цільової функції в симплексній таблиці враховується при виборі рядка для побудови правильного відсікання;

2) справедливо одне із двох тверджень: або цільова функція  обмежена знизу на С_o, або задача (£^ц, C) має хоча б один план х'.

Тоді перший алгоритм Гомори вимагає кінцевого числа більших ітерацій.

Похожие работы

Оптимизация показателей

Скачать

9885

18

21

4 9 0 1 0 3 Р5 0 8 4 -2 0 0 1 4 F 0 -5 -6 0 0 0 Таблиця № 1 – Вихідна симплекс-таблиця Знаходження оптимального розвязку ЗЛП за допмогою с-м включає слідуючі етапи: 1.   За вихідною с-т знаходять опорне рішення Кожній с-т відповідає своє опорне рішення. Воно може бути представлене у вигляди вектора Х Розмірніст вектора дорівнює кількості змі ...

Мова програмування Assembler

Скачать

206879

0

16

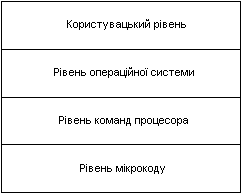
... . Механізм переривань забезпечує ефективна взаємодія пристроїв уведення-висновку з мікропроцесором. Переривання цікавлять нас тому, що обробка переривань - це прерогатива програмування на мові асемблера. У високорівневих мовах відсутні засоби роботи з перериваннями на машинному рівні. Переривання звичайно викликаються зовнішніми пристроями. Переривання сигналізує мікропроцесору, щоб він призупинив ...

Процес підвищення ефективності функціонування підприємства ЗАТ "Запоріжтрансформатор" з багатономенклатурним виробництвом

Скачать

176822

12

5

... рішень, зв’язаних із регулюванням витрат і з питань інвестиційної діяльності підприємства. Отже, управлінський облік це формування інформації для управління витратами з метою підвищення ефективності функціонування підприємства. Причому, відповідно до Закону «Про бухгалтерський облік і фінансову звітність в Україні», підприємства вправі самостійно обирати систему і форми ведення управлінського ...

Розподіл Пуасона

Скачать

24260

1

0

... ‚ є гіпотезою про закон розподілу. Гіпотеза про те‚ що середні розміри деталей‚ які виготовляються на однотипних‚ паралельно працюючих станках‚ приблизно однакові‚ є гіпотезою про параметри розподілу. Зроблений на основі статистичних даних висновок про те‚ що між кількома генеральними сукупностями або між емпіричним і теоретичним розподілом істотних відмінностей немає‚ називають нульовою ( ...