Алгоритм Данцига

6. Алгоритм Данцига

Спосіб побудови правильних площин, що відтинають, запропонованим Данцигом значно простіше, ніж всі викладені вище способи. Але, як показали Гомори й Гофман, кінцівка алгоритму Данцига гарантується лише для дуже вузького класу задач. На прикладі алгоритму Данцига видно, наскільки тонким є питання про побудову правильних відсікань і як обережно варто підходити до різним спрощеним алгоритмам.

Розглядається повністю цілочисленна задача лінійного програмування:

Максимізувати

(39)

при умовах

(40)

(41)

 – цілі, (42)

Ранг матриці  вважаємо рівним m.

Теорема. Нехай x(£_r, C)=x^r є оптимальним опорним планом задачі (£_r, C) і x^r не задовольняє умові цілочисленності, N_r – множина індексів, що нумерують небазисні змінні, відповідні x^r.

Тоді нерівність

(43)

є правильним відсіканням.

Правильне відсікання, що відтинає нецілочисленний оптимум x(£_r, C) задачі (£_r, C), можна записати в такий спосіб:

 

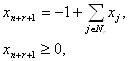
 – ціле.

Помітимо, що кожна із знову змінних  однозначно визначається завданням змінних , так що .

Позначимо через  упорядковані в порядку зростання компоненти  плану x задачі (39) – (41), так що

(44)

Покладемо

 

(45)

Лема. Якщо для деякого плану x задачі (39) - (41)

 

, (46)

те

(47)

 

Доказ проведемо по індукції. Спочатку доведемо, що

(47¢)

По визначенню

(48)

Тому що ранг матриці  дорівнює m, те

де  – число елементів множини . З визначення чисел  одержуємо

(49)

(50)

З (48), (49), (50) і (46) маємо

Лема доведена при р=1.

Тепер допустимо, що лема вірна при , і доведемо неї при :

Лема доведена.

Користуючись лемою, доведемо дві теореми.

Теорема 1. Якщо кожний оптимальний план задачі (39) – (42) містить не менш (m+2) позитивних компонентів, то алгоритм Данцига не буде кінцевим.

Доказ. Допустимо, що на s-й ітерації алгоритму Данцига вийде шуканий оптимальний план . Розглянемо числа

(51)

Всі вони цілі й серед них повинне бути (n-m) нулів – це небазисні змінні . Крім того, за умовою серед чисел , повинне бути принаймні (m+2) позитивні числа, тобто не більше чим (n-m-2) нулів.

По визначенню чисел  звідси треба, що

а тому що  повинне бути цілим, те

(52)

Але по визначенню чисел

(53)

З (52) одержуємо

(54)

і по лемі

(55)

З (52), (53) і (55) треба, що серед чисел (51) принаймні [1+(m+1)+s] = [m+2+s] позитивних, а отже, не більше чим [n+s – (m+2+s)] = (n-m-2) нулів. Але вище було відзначено, що серед чисел (51) повинне бути (n-m) нулів. Вийшло протиріччя. Теорема 1 доведена.

Наслідок (з теореми 1). Для того щоб алгоритм Данцига був кінцевим, необхідно, щоб шуканий оптимальний план лежав на ребрі багатогранної множини (40) - (41) (передбачається, що задача (39) - (41) невиродженна).

Хоча ця умова і є досить твердим, йому задовольняють, наприклад, всі (невиродженні) задачі наступного виду.

Максимізувати

(56)

при умовах

(57)

(58)

(59)

 – ціле, (60)

А це важливий клас задач.

Однак наведене в наслідку необхідна умова кінцівки алгоритму Данцига не є достатнім. Дійсно, має місце наступна

Теорема 2. Якщо для деякого оптимального плану x' задачі (39) - (42) і деякого плану x» задачі (39) - (41) мають місце нерівності

 

(61)

и

(62)

те алгоритм Данцига не буде кінцевим.

Доказ. Допустимо, що алгоритм Данцига кінцевий. Тоді з (61) треба, що крапка x» була відсічена на якійсь (скажемо, р-й) ітерації, так що

(63)

Але з (62) і леми одержимо

(64)

Порівнюючи (63) і (64), одержуємо протиріччя. Теорема 2 доведена.

Отже, спрощений алгоритм Данцига буде кінцевим лише в досить рідких випадках.