Другий алгоритм Гомори

4. Другий алгоритм Гомори

Другий алгоритм Р. Гомори призначається для рішення задач, у яких вимога цілочисленності накладена на деякі змінні (зокрема й на все). Ми його розглянемо стосовно до задач частково цілочисленного типу, розуміючи, що обчислювальна схема буде справедливої й для задач, повністю цілочисленних.

Нехай в області, певної умовами:

(20)

(21)

 – цілі, (22)

потрібно максимізувати функцію

(23)

Метод рішення задачі (20–23) ґрунтується на тій же ідеї, що й метод рішення повністю цілочисленних задач. А саме: будується область £_k, що при k = 0 визначається умовами (20–21); вирішується отримана при цьому задача лінійного програмування (20–21, 23). Якщо задача (20–21, 23) виявляється розв'язної, то отримане оптимальне рішення її аналізується на допустимість для вихідної задачі цілочисленного програмування (20–23). Якщо знайдене рішення виявляється целочисленным, то одночасно воно буде оптимальним для (20–23). Якщо оптимальне рішення (£_k, C) – задачі виявляється неприпустимим для вихідної задачі (20–23), те здійснюється побудова правильного відсікання й перехід до рішення нової задачі,

Другий алгоритм Р. Гомори формулюється у вигляді наступної теореми:

Теорема. Нехай х(£_k, C) – оптимальне рішення (£_k, C) – задачі,  – елементи відповідної йому симплексної таблиці. Якщо  – неціле , то

(24)

 – ціле, (25)

де

(26)

визначає правильне відсікання. Блок-схема другого алгоритму Р. Гомори аналогічна блок-схемі першого алгоритму Р. Гомори й відрізняється лише правилом побудови коефіцієнтів правильного відсікання.

Правило побудови правильного відсікання

Нехай x(£_k, C) не задовольняє умові цілочисленності,  – елементи симплексної таблиці, що відповідає отриманому оптимальному рішенню (£_k, C) – задачі. Виберемо i₀=min {i | i Î (1, 2,…,n),x_i0^k–неціле} і будуємо правильне відсікання по формулах (24 – 26).

Умови кінцівки другого алгоритму Гомори:

1) Цільова функція F(x) задовольняє умові цілочисленності. Це враховується при виборі рядка k для побудови правильного відсікання.

2) Виконано принаймні одне із двох умов:

2') цільова функція обмежена знизу на багатогранній множині £= £₀;

2») задача (£₀^ц, C) має принаймні один план.

За допомогою другого алгоритму Гомори можна (у випадку n₁=n) вирішувати й повністю цілочисленну задачу лінійного програмування. Однак у цьому випадку немає підстав для порівняння ефективності другого й першого алгоритмів Гомори.

5. Алгоритм Дальтона й Ллевелина

Другий алгоритм Гомори має справа із частково цілочисленними задачами лінійного програмування. Дальтон і Ллевелин розглядають широкий клас задач - частково дискретні задачі лінійного програмування й стосовно до них модифікують другий алгоритм Гомори.

Нагадаємо, що рішенням задачі дискретного програмування будемо називати вектор, координати якого належать £^ц області виду:

(27)

(28)

(29)

і максимізує значення функції

(30)

Будемо припускати, що , тобто  і є наперед заданими числами.

Теорема. Нехай x(£_k, C) – оптимальне рішення задачі (27–28, 30),  – елементи симплексної таблиці, що відповідає йому.

Якщо x(£_k, C) є неприпустимим рішенням задачі (27–30) і , тоді, використовуючи i-ю рядок симплексної таблиці, можна побудувати відсікання, що володіє властивістю правильності по формулах:

(31)

(32)

де

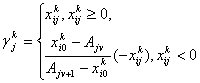(33)

Доказ. Перевіримо спочатку умову відсікання. Нехай в оптимальному рішенні x(£_k, C) координата  не задовольняє умові (29). Покажемо, що в цьому випадку вектор х(£_k, C) не задовольняє умовам (31, 32). Оскільки N_k – множина індексів небазисних змінних x_i, які в оптимальному рішенні дорівнюють нулю, то рівність (31) приймає вид  і буде негативним відповідно до умови теореми. Отже, , тобто умова відсікання не виконується.

Перевіримо умову правильності. Для цього покажемо, що будь-яке припустиме рішення задачі (27-30) задовольняє умовам (31, 32).

Запишемо розкладання для координати припустимого рішення задачі (27-30) по небазисним змінним

(34)

і розглянемо два випадки: a) ; б) . Уведемо позначення:

і представимо (34) у вигляді

де

Очевидно,  тому що .

Розглянемо випадок а): , або що однаково, .

Звідси Але тому

(35)

Помножимо обидві частини (35) на ненегативну величину  й складемо з ненегативною величиною :

(36)

Розглянемо випадок б):  або, що однаково,  Тому що по визначенню , то  Помножимо обидві частини нерівності  на ненегативну величину  й на -1, одержимо . Додаючи до отриманого вираження нерівність , одержимо

(37)

Таким чином, в а) і в б) випадках прийшли до тому самому нерівності (36) і (37). Користуючись раніше уведеними позначеннями, їх можна записати

(38)

Формула (38) визначає правильні відсікання. Порівнюючи її з вираженням (31–32), доходимо висновку, що коефіцієнти визначаються в такий спосіб:

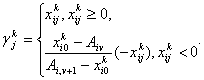
Теорема доведена.

Алгоритм Дальтона - Ллевелина може бути описаний у такий спосіб.

1. Вирішується (£_k, C) – задача (27–30) (спочатку k = 0). Нехай x(£_k, C), k = 0, 1, 2,…оптимальне рішення (£_k, C) – задачі,  – симплексна таблиця.

2. Перевіряється умова допустимості по всіх координатах оптимального вектора рішення х(£_k, C) (£_k, C) – задачі. Якщо умова допустимості виконується, то отримане рішення є оптимальним рішенням вихідної задачі (27-30). Якщо умова допустимості не виконується хоча б по одній координаті, здійснюється перехід до 3.

3. Нехай  не задовольняє умові допустимості. Тоді вибирається

 

i₀ = min {i| 1<i<n₁, х_j0^k – не задовольняє (29)}.

4. Для обраного номера i=i₀ будується правильне відсікання, тобто вводиться додаткова змінна

де визначається формулою (33),

5. Додаємо лінійне обмеження, що визначає правильне відсікання, до умов (£_k, C) – задачі й одержуємо нову (£_{k+1, C) – задачу. Думаючи k = k + 1, переходимо до п. 1.}

Приведемо без доказу теорему про кінцівку алгоритму.

Теорема. Якщо: коефіцієнти цільової функції дискретні; F(x) обмежена знизу на багатогранній множині £; задача (£, C) має принаймні одне рішення; вибір рядка для побудови правильного відсікання виробляється за правилом мінімального номера й (£_k, C) – задачі вирішуються методом послідовного уточнення оцінок, то алгоритм Дальтона й Ллевелина сходиться.