Навигация
Изменение коэффициентов целевой функции
3. Изменение коэффициентов целевой функции
Базисная переменная
Изменение коэффициента целевой функции базисной переменной влияет на оценки плана небазисных переменных. Для базисной переменной диапазон устойчивости, в котором может меняться cj, оставляя оптимальным текущее решение, задается выражением: ![]() где
где
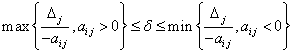
Если нет коэффициентов ![]() то
то ![]()
Если нет коэффициентов ![]() то
то ![]()
1) X1
c1=25
![]()
![]()
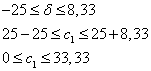
2) X2
C2=20

Нет коэффициентов ![]() то
то ![]()

3) X3
C3=50

Нет коэффициентов ![]() то
то ![]()

4) X5
C5=0

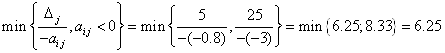
![]()
5) X6
C6=0
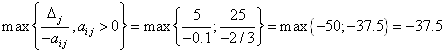

![]()
6) X7
C7=0
![]()
![]()
![]()
Небазисная переменная
Для небазисной переменной диапазон устойчивости в котором cj может меняться, оставляя текущее решение оптимальным задается выражением:
![]() где
где
![]()
![]() -оценка плана переменной
-оценка плана переменной ![]() , отвечающее оптимальному решению.
, отвечающее оптимальному решению.
1) x4 с4=0
![]() =5
=5
![]()
![]()
2) Х8 с8=0
![]() =5
=5
![]()
![]()
3) Х9 с9=0
![]() =25
=25
![]()
![]()
4. Изменение компонент вектора ограничений
базисная дополнительная переменная.
Если дополнительная переменная i-го ограничения базисная, то ее значение дает диапазон изменения, в котором соответствующая компонента bi может уменьшаться (увеличиваться, если ограничение ≥)
Решение остается оптимальным в диапазоне:
![]() где
где
![]() для ограничения ≤
для ограничения ≤
![]() для ограничения ≥
для ограничения ≥
где ![]() -значение соответствующее дополнительной пересенной
-значение соответствующее дополнительной пересенной
1) Х5 в2=600
![]() ограничение ≤
ограничение ≤
![]()
![]()
![]()
2) Х6 в3=150
![]()
![]()
![]()
![]()
3) Х7 в4=50
![]()
![]()
Небазисная дополнительная переменная: ![]()
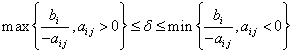
1) x4
b1=400
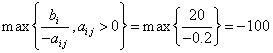

![]()
![]()
2) x8
b5=50
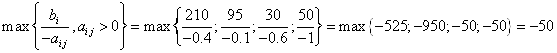

![]()
![]()
![]()
3) x9
b6=30

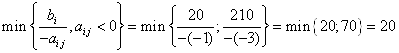
![]()
![]()
![]()
1) От итоговой симплекс-таблицы прямой задачи перейдем к решению двойственной.
Сформулируем двойственную задачу:
- Так как прямая задача- задача на максимум, то двойственная ей задача на минимум.
- Коэффициенты функции цели прямой задачи будут коэффициентами вектора ограничений для двойственной.
- Коэффициенты вектора ограничений прямой задачи будут коэффициентами функции цели для двойственной.
- Ограничения двойственной задачи будут иметь знак ≥
| Прямая задача |
|
|
| Двойственная задача |
|
|
Для удобства перехода между прямой и двойственной задачами подпишем внутри последней симплекс-таблицы соответствующие переменные двойственной задачи
| БП | U7 | U8 | U9 | U1 | U2 | U3 | U4 | U5 | U6 | |||
| Двойств | Вi | A1 | А2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | ||
| 1 | A1 | U7 | 20 | 1 | 0 | 0 | 0,2 | 0 | 0 | 0 | -0,6 | -1 |
| 2 | A5 | U2 | 210 | 0 | 0 | 0 | -0,8 | 1 | 0 | 0 | 0.4 | -3 |
| 3 | A6 | U3 | 95 | 0 | 0 | 0 | -0,2 | 0 | 1 | 0 | 0,1 | 2/3 |
| 4 | A7 | U4 | 30 | 0 | 0 | 0 | -0,2 | 0 | 0 | 1 | 0.6 | 1 |
| 5 | A2 | U8 | 50 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 6 | A3 | U9 | 30 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| ∆j=W(j)-cj | 3000 | 0 | 0 | 0 | 5 | 0 | 0 | 0 | 5 | 25 | ||
Итоговая симплекс-таблица двойственной задачи:
| БП | Сбаз | Вi | C1=400 | С2=600 | C3=150 | C4=50 | C5=50 | C6=30 | C7=0 | C8=0 | C9=0 | |
| U1 | U2 | U3 | U4 | U5 | U6 | U7 | U8 | U9 | ||||
| 1 | U1 | 400 | 5 | 1 | 0.8 | 0.2 | 0.2 | 0 | 0 | -0.2 | 0 | 0 |
| 2 | U5 | 50 | 5 | 0 | -0.4 | -0.1 | -0.6 | 1 | 0 | 0.6 | -1 | 0 |
| 3 | U6 | 30 | 25 | 0 | 3 | -2/3 | -1 | 0 | 1 | 1 | 0 | -1 |
| ∆j=Z(j)-cj | 0 | -210 | -95 | 30 | 0 | 0 | -20 | -50 | -30 | |||
Оптимальным решением двойственной задачи будет:
| Свободные переменные | Базисные переменные |
| U2=0 U3=0 U4=0 U7=0 U8=0 U9=0 | U1=5 U5=5 U6=25 |

5) Целочисленное решение методом отсечения.
Так как в ходе решения нами было найдено целочисленное решение задачи максимум, то поставленная перед нами задача полностью решена!
Для получения максимальной прибыли рекомендуется выпускать изделия в следующем ассортименте:
Изделия Типа 1 в размере х1=20 шт
Изделия Типа 2 в размере х2=50 шт
Изделия Типа 3 в размере х3=30 шт
При таком выпуске прибыль будет максимальна и составит W*=3000 $
Похожие работы
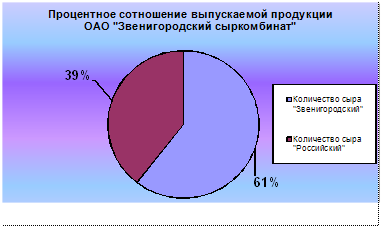
... ). Основным меню является форма, в которую пользователь попадает при нажатии кнопки ²Старт² заставки. На ней отображается название главного меню, "Оптимальное планирование выпуска продукции ОАО Звенигородского сыркомбината"², и элементы управления, которые позволяют перемещаться к различным составным частям приложения, из которых, в свою очередь, реализованы переходы назад в главное ...
... же ценообразования остается прежним: анализ спроса и предложения, проект цены, исходя из ситуации на рынке, и формирование контрактной цены в ходе непосредственных переговоров поставщика и потребителя. 3 Анализ политики ценообразования на продукцию ОАО «Нижнекамскшина» 3.1 Общая характеристика деятельности предприятия ОАО «Нижнекамскшина» ОАО «Нижнекамскшина» - крупнейшее предприятие в ...
... плана по его уровню, определить влияние факторов на его прирост и на этой основе дать оценку работы предприятия по использованию возможностей и установить резервы снижения себестоимости продукции. Управление расходами – процесс целенаправленного формирования расходов по их видам, местам возникновения и носителям для постоянного контроля уровня расходов и стимулирования их снижения. РАЗДЕЛ 2. ...
... ситуации является определяющим фактором [7]. В зависимости от того, какой метод анализа модели выбран, факторныe разложения могут различаться. Глава 2. Применение детерминированных экономико-математических моделей и методов факторного анализа на примере РУП «ГЗЛиН». 2.1 Характеристика РУП «ГЗЛиН» 9 октября 1979 - издан приказ М 272 Министерства машиностроения для животноводства и ...
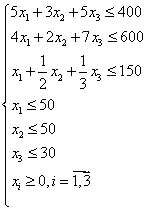
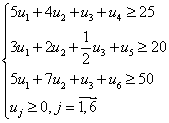


0 комментариев