Линейные метрические, нормированные и унитарные пространства

Линейные метрические, нормированные и унитарные пространства

Введение

При решении многих технических и прикладных задач радиотехники возникают вопросы: как объективно сравнить какой сигнал больше другого или как оценить "близость" двух сигналов.

Оказывается, что методы функционального анализа, создав стройную теорию сигналов, в основе которой лежит концепция сигнала как элемента специально сконструированного пространства, позволяют ответить на эти вопросы.

Введем обозначения. Если R – некоторое множество элементов, то f Î R означает, что f является элементом R;  или f Ï R означает, что f не принадлежит R.

Множество элементов х Î R, обладающих свойством А обозначается символом  например  - множество точек, принадлежащих полукругу х² + y² £ 1, x ³ 0.

Если M и N – два множества, то прямое произведение M х N этих множеств определяется следующим образом

то есть представляет собой множество всех упорядоченных пар (x, y), где x Î M, a y Î N.

1. Линейные метрические пространства

Множество R называется линейным пространством, если

1) в R определена операция "сложения", которая подчиняется всем правилам сложения: если f Î R, g Î R, то f + g Î R; в R имеется нулевой элемент 0 такой, что 0 +f = f для всех f Î R;

2) в R определена операция умножения элемента f Î R на числа a из множества К (a Î К, f Î R Þ a f Î R). Чаще всего К – множество всех действительных или комплексных чисел.

В дальнейшем будем рассматривать только линейные пространства.

Рассмотрим отображение Т, которое каждому элементу f Î R однозначно ставит в соответствие элемент h Î R*, где R* является также линейным пространством. Если R* = R, то Т отображает R в самого себя. Отображение Т называется оператором и отображение R в R* записывается в виде уравнения

T f = h (f Î R, h Î R*).

В частном случае, когда R* - пространство комплексных чисел, Т носит название функционала.

Пусть уравнение

T f = h

имеет единственное решение и каждому элементу h Î R* можно поставить в соответствие единственный элемент f Î R. Оператор, осуществляющий это соответствие, называется обратным по отношению к Т и обозначается Т^-1. Таким образом можно записать

f = T^-1 h.

Пример. Пусть имеется система линейных уравнений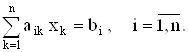

Представим эту систему в матричном виде

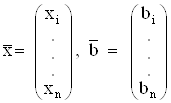
Если ввести пространство матриц – столбцов R, то  где

и  Здесь оператор А – матрица размера n x n

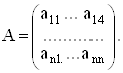
Если матрица А невырождена, то обратная матрица и является обратным оператором:

Определение. Линейное пространство R называется метрическим, если каждой паре элементов х, y Î R ставится в соответствие вещественное число r (x, y) – расстояние между x и y – удовлетворяющее условиям:

1.  r (x, y) ³ 0, если r (x, y) = 0, то x = y;

2.  r (x, y) = r (y, x);

3.  r (x, y) £ r (x, z) + r (z, y) (неравенство треугольника).

Если введением расстояния пространство R превращено в метрическое пространство, то говорят, что в пространстве R введена метрика.

В радиотехнике элементами пространства являются сигналы (токи или напряжения), математическими моделями которых являются функции времени x(t), y(t), ... . Рассмотрим следующее пространство сигналов.

1. С_{[a, b]} - пространство непрерывных на промежутке [a, b] функций с метрикой:

 y(t)

r(x,y)

2. L²_{(a, b)} - пространство интегрируемых в квадрате функций (x(t) Î L²_{(a, b)}, если  с метрикой

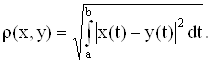
Определение. Элементы линейного пространства R называются линейно независимыми, если из условия

следует, что

a₁ = a₂ = . . . = a_n = 0.

В противном случае элементы f₁, f₂, . . . , f_n считаются линейно зависимыми.

Максимальное число линейно независимых элементов определяет размерность dim R пространства R и образуют базис этого пространства. Если m = dim R, то пространство обозначается R_m.