Навигация
Линейные нормированные пространства
2. Линейные нормированные пространства
Определение. Линейное пространство R называется нормированным, если каждому элементу х Î R ставится в соответствие вещественное число ![]() ("длина" элемента х), называемое нормой х, которое удовлетворяет условиям:
("длина" элемента х), называемое нормой х, которое удовлетворяет условиям:
1. ![]() , тогда х = 0;
, тогда х = 0;
2. ![]() (однородность нормы);
(однородность нормы);
3. ![]() (неравенство треугольника).
(неравенство треугольника).
Положив для ![]()
![]()
превращаем нормированное пространство R в метрическое.
Можно и метрическое пространство R превратить в нормированное, если метрика удовлетворяет условиям:
![]()
![]() положив
положив ![]()
Рассмотренные ранее пространства сигналов С[a,b] и L2(a,b) становятся соответственно нормированными, если
![]()
![]()
![]()
и ![]()

Если положить а = ¥, b = ¥, то квадрат этой нормы в теории сигналов носит название энергии сигнала.

так как такая энергия выделяется на резисторе с сопротивлением в 1 Ом при напряжении x(t) на его зажимах.
Пример. Имеется треугольный импульс длительности t:
![]()
Вычислить энергию и норму сигнала.
Решение.

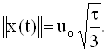
3. Линейное унитарное пространство
Определение. Линейное нормированное пространство R называется унитарным, если в нем введено скалярное произведение, которое каждой паре элементов x, y Î R ставит в соответствие действительное или комплексное число (x, y), удовлетворяющее условиям
1. (x, y) = (y, x)* ( * - знак комплексного сопряжения);
2. (a1 х1 + a2 х2, y) = a1(x1, y) + a2(x2, y) (a1, a2 Î K);
3. (x, x) ³ 0, если (х, х) = 0, то х = 0.
В унитарном пространстве норма вводится следующим образом
![]()
Теорема 1. Для " х, y унитарного пространства R справедливо неравенство Шварца
![]()
Равенство имеет место лишь для линейно зависимых элементов.
Теорема 2. Для " х, y унитарного пространства R имеет место неравенство
![]()
Равенство имеет место, если один из элементов х или y равен нулю или, когда х = l y (l > 0).
Теорема 3. Для " х, y унитарного пространства R выполняется равенство параллелограмма
![]()
Равенство имеет место, если один из элементов х или y равен нулю или, когда х = l y (l > 0).
Определение. Два элемента х, y Î R (x ¹ 0, y ¹ 0) называются ортогональными, если (х, y) = 0.
Система элементов e1, e2, . . . , en, . . . унитарного пространства R называется ортонормированной, если
![]()
Пусть система элементов х1, х2, . . . , хn, . . . ортогональна ((xi, xj)=0, i ¹ j), тогда ее можно нормировать, положив

Из ортонормированности системы следует ее линейная независимость. Обратно – любую линейно независимую систему можно ортонормировать. Процесс ортонормированности следующий. Если система элементов y1, y2, . . . , yn, . . . –линейно независимая, то система e1, e2, . . . , en, . . ., где
![]()
становится ортонормированной.
Пусть теперь f – любой элемент унитарного пространства R, a e1, e2, ..., en,... – ортонормированная система этого пространства. Величина
![]()
носит название коэффициента Фурье, а ряд
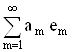
носит название ряда Фурье. Ряд Фурье наилучшим образом аппроксимирует f (приближается к f). Это значит, если рассматривать норму разности элемента f и ряда Фурье

то наименьшее значение норма примет при
![]()
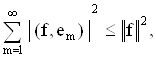
которое называется неравенством Бесселя.
Примеры ортонормированных систем:
1. Система гармонических функций, записанных в комплексном виде
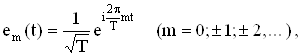
образуют ортонормированную систему в ![]()
2. Функции
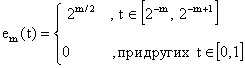
образуют для m = 1, 2, 3, ...ортонормированную систему, состоящую из неотрицательных функций на отрезке [0,1].
3. Ортонормированная система функций Уолша wal(m, x) ![]() заданная на интервале
заданная на интервале 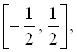 широко используется при дискретной обработке сигналов. Аналитическое описание функций Уолша довольно сложно. Легко понять принцип построения этих функций из графиков
широко используется при дискретной обработке сигналов. Аналитическое описание функций Уолша довольно сложно. Легко понять принцип построения этих функций из графиков
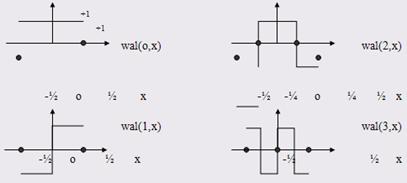
4. Важный класс ортонормированных систем можно получить при помощи ортогонализации функций 1, t, t2, ..., tn, ... в унитарном пространстве ![]() со скалярным произведением
со скалярным произведением

где р(t) – некоторая положительная, непрерывная на интервале [a, b] функция. Для отрезка [-1, 1] и p(t) = 1 получаем полиномы Лежандра; для отрезка [-1, 1] и ![]() - полиномы Чебышева первого рода; для полупрямой [0, ¥] и p(t) = е-t – полином Лягерра; для всей оси (-¥, ¥) и p(t) = е-t – полином Эрмита и т.д.
- полиномы Чебышева первого рода; для полупрямой [0, ¥] и p(t) = е-t – полином Лягерра; для всей оси (-¥, ¥) и p(t) = е-t – полином Эрмита и т.д.
Определение. Линейное метрическое пространство R называется полным, если оно содержит все предельные точки. Это значит, если r(хm+p, xn) ® 0 при m ® ¥ (xm Î R), " p = ![]() , то $ хо Î R такое, что lim r(xm, xo) = 0.
, то $ хо Î R такое, что lim r(xm, xo) = 0.
m ®¥
Определение. Полное метрическое пространство называется пространством Банаха.
Полное унитарное пространство носит название пространства Гильберта.
Примеры.
1. Пространство L(a, b) – абсолютно интегрируемых на интервале (а, b) функций (x(t) Î L(a, b), если 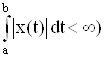 с метрикой
с метрикой
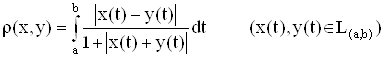
является пространством Банаха.
3. Пространство L2(a, b), со скалярным произведением
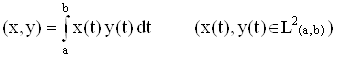
является пространством Гильберта.
Похожие работы
... несколько уравнений, а в каждом уравнении - несколько переменных. Задача оценивания параметров такой разветвленной модели решается с помощью сложных и причудливых методов. Однако все они имеют одну и ту же теоретическую основу. Поэтому для получения начального представления о содержании эконометрических методов мы ограничимся в последующих параграфах рассмотрением простой линейной регрессии. ...
... , называется оператором сдвига, если он каждую последовательность вида (х1,х2,…, хn…) переводит в последовательность вида (0, х1, х2, …, хn…), т.е. выполняется равенство: (х1,х2,…, хn…)=(0, х1, х2, …, хn…). Можно также рассматривать оператор сдвига, который действует в пространстве последовательностей, бесконечных в обе стороны. Элемент этого пространства можно представить в таком виде: (…х-2, ...
... и территориальное (географическое) разделение труда. Определение понятий. Международное разделение труда (МРТ) как вид территориального разделения труда. Его роль в географии мирового хозяйства и мирохозяйственной реальности. Географическое (территориальное) разделение труда - пространственная форма общественного разделения труда, выражающаяся в специализации отдельных районов и стран на ...
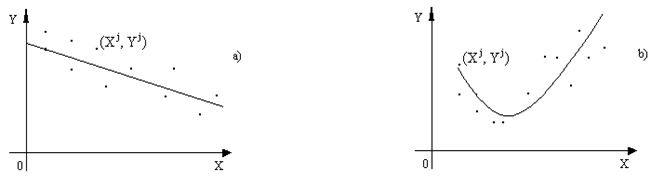
0 комментариев