Навигация
Введение
Тема для написания дипломной работы была выбрана не случайно. Теория линейных операторов – это интересная и важная область, которая позволяет не только активно применять уже имеющиеся знания по анализу, но и узнать много нового.
В данной работе рассматриваются линейные операторы одностороннего и двустороннего сдвига. Вводятся основные понятия: спектр, резольвента, спектральный радиус оператора. Рассматриваются задачи, в ходе решения которых выясняются некоторые свойства спектров операторов сдвига. Определяется класс взвешенных сдвигов, выводится соотношение для нормы и спектрального радиуса оператора взвешенного сдвига.
Известно, что если рассматривать поле действительных чисел при условии, что аксиома Архимеда не выполняется, то получим новое, расширенное поле, в котором существуют бесконечно большие и бесконечно малые элементы. На основании этого расширения можно построить весь математический анализ – нестандартный анализ.
Естественно, часть основных понятий и свойств линейных операторов было бы интересно определить и доказать и в нестандартном анализе, что и было сделано в работе.
В частности, был установлен следующий факт: хотя стандартный оператор сдвига не имеет собственных векторов, но его нестандартное расширение имеет «почти собственные» векторы, т. е. векторы, в определенном смысле бесконечно близкие к собственным.
Часть 1. Оператор сдвига в гильбертовом пространстве
§1. Основные понятия и факты теории линейных операторов
1. Определение и примеры линейных операторов
Пусть Е и Е1 – два линейных нормированных пространства над полем комплексных чисел. Линейным оператором, действующим из Е в Е1 называется отображение ![]() (
(![]() удовлетворяющее условию
удовлетворяющее условию
![]() для всех
для всех ![]() .
.
Совокупность DA всех тех ![]() , для которых отображение А определено, называется областью определения оператора А; вообще говоря, не предполагается, что DA=E , однако мы всегда будем считать, что DA есть линейное многообразие, то есть, если х,у
, для которых отображение А определено, называется областью определения оператора А; вообще говоря, не предполагается, что DA=E , однако мы всегда будем считать, что DA есть линейное многообразие, то есть, если х,у![]() DA , то и
DA , то и ![]() при любых
при любых ![]() .
.
Определение 1. Оператор ![]() называется непрерывным в точке х0
называется непрерывным в точке х0 ![]() DA , если для любой окрестности V точки у0=Ах0 существует такая окрестность U точки х0 , что Ах
DA , если для любой окрестности V точки у0=Ах0 существует такая окрестность U точки х0 , что Ах![]() V , как только х
V , как только х![]() . Оператор А называется непрерывным, если он непрерывен в каждой точке х
. Оператор А называется непрерывным, если он непрерывен в каждой точке х![]() DA.
DA.
Поскольку Е и Е1 – нормированные пространства, то это определение равносильно следующему: оператор А называется непрерывным, если выполняется следующее условие: ![]() (
(![]()
![]()
![]()
![]() .
.
Примеры линейных операторов
Пусть А – линейный оператор, отображающий n-мерное пространство Rn c базисом е1, …, еn в m-мерное пространство Rm с базисом f1, …,fm . Если х – произвольный вектор из Rn , то 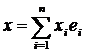 и, в силу линейности оператора А
и, в силу линейности оператора А ![]()
![]() .
.
Таким образом, оператор А задан, если известно, в какие элементы он переводит базисные векторы е1,…, еn . Рассмотрим разложение вектора Аеi по базису f1, …, fm . Имеем 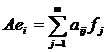 . Следовательно, оператор А определяется матрицей коэффициентов аij . Образ пространства Rn и Rm представляет собой линейное пространство, размерность которого равна, очевидно, рангу матрицы
. Следовательно, оператор А определяется матрицей коэффициентов аij . Образ пространства Rn и Rm представляет собой линейное пространство, размерность которого равна, очевидно, рангу матрицы ![]() , т.е. во всяком случае не превосходит n (свойство ранга матрицы). Отметим, что в конечномерном пространстве всякий линейный оператор автоматически непрерывен.
, т.е. во всяком случае не превосходит n (свойство ранга матрицы). Отметим, что в конечномерном пространстве всякий линейный оператор автоматически непрерывен.
Рассмотрим гильбертово пространство Н и в нем некоторое подпространство Н1 . Разложив Н в прямую сумму подпространства Н1 и его ортогонального дополнения, т.е. представив каждый элемент ![]() в виде
в виде ![]() (
(![]() положим Рh=h1. Этот оператор Р естественно назвать оператором проектирования, проектирующим все пространство Н на Н1. Очевидно, что Р является линейным и непрерывным оператором.
положим Рh=h1. Этот оператор Р естественно назвать оператором проектирования, проектирующим все пространство Н на Н1. Очевидно, что Р является линейным и непрерывным оператором.
Рассмотрим в пространстве ![]() непрерывных функций на отрезке [a;b] с нормой
непрерывных функций на отрезке [a;b] с нормой ![]() оператор, определяемый формулой
оператор, определяемый формулой
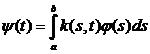 , (1)
, (1)
где k(s,t) – некоторая фиксированная непрерывная функция двух переменных. Функция ![]() непрерывна для любой непрерывной функции
непрерывна для любой непрерывной функции ![]() , так что оператор (1) действительно переводит пространство непрерывных функций в себя. Его линейность очевидна. Можно доказать также, что он непрерывен.
, так что оператор (1) действительно переводит пространство непрерывных функций в себя. Его линейность очевидна. Можно доказать также, что он непрерывен.
Тот же оператор можно рассмотреть на множестве непрерывных функций С2[a,b] с нормой 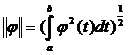 , где он также непрерывен.
, где он также непрерывен.
4. Один из важнейших для анализа примеров линейных операторов – оператор дифференцирования. Его можно рассматривать в пространстве C[a,b] : Df(t) = ![]() .
.![]() Этот оператор D определен не на всем пространстве непрерывных функций, а лишь на линейном многообразии функций, имеющих непрерывную производную. Оператор D линеен, но не непрерывен. Это видно, например, из того, что последовательность
Этот оператор D определен не на всем пространстве непрерывных функций, а лишь на линейном многообразии функций, имеющих непрерывную производную. Оператор D линеен, но не непрерывен. Это видно, например, из того, что последовательность ![]() сходится к 0 ( в метрике С[a,b]), а последовательность
сходится к 0 ( в метрике С[a,b]), а последовательность ![]() не сходится.
не сходится.
Оператор дифференцирования можно рассматривать как оператор, действующий из пространства D1 непрерывно дифференцируемых функций на [a,b] с нормой ![]() в пространство С[a,b]. В этом случае оператор D линеен и непрерывен и отображает все D1 на все С[a,b].
в пространство С[a,b]. В этом случае оператор D линеен и непрерывен и отображает все D1 на все С[a,b].
Рассмотрение оператора дифференцирования как оператора, действующего из D1 в С[a,b], не вполне удобно, так как, хотя при этом мы и получаем непрерывный оператор, определенный на всем пространстве, но не к любой функции из D1 можно применять этот оператор дважды. Удобнее рассматривать оператор дифференцирования в еще более узком пространстве, чем D1 , а именно в пространстве ![]() бесконечно дифференцируемых функций на отрезке [a; b], в котором топология задается счетной системой норм
бесконечно дифференцируемых функций на отрезке [a; b], в котором топология задается счетной системой норм ![]() . Оператор дифференцирования переводит все это пространство в себя, и, как можно проверить, он непрерывен на этом пространстве.
. Оператор дифференцирования переводит все это пространство в себя, и, как можно проверить, он непрерывен на этом пространстве.
Похожие работы
... непрерывных и ограниченных функций – C[], заданный следующим образом: Af(x) = f(x+a). Функции f(x), f(x+a) C[], a R, f(x+a) – непрерывная и ограниченная функция. Покажем линейность оператора А, по определению 1 должны выполняться следующие аксиомы : 1) Аксиома аддитивности: А(f+g) = А(f) + А(g). А(f+g) = (f+g)(x+a) = f(x+a) + g(x+a) = А(f) + А(g). По определению суммы функции, аксиома ...
... В этих формулах привлекательно то, что результат произведения двух операторов сдвигов выражается через операторы с действительными собственными значениями, как это следует из сопоставления правых частей уравнений (4.92) – (4.94), с одной стороны, и уравнений (4.90) и (4.91) – с другой. 4.3.5.13. Все коммутационные соотношения операторов момента импульса и его проекций, найденные в этом разделе,
... проектора Q пространства L на H, что tQ = Qt для любого вещественного s. (4). Найдем вид проектора. Положим e(x)=e . Тогда te=ee, а так как оператор Q линеен, то Qte = eQe. (5). Из (4) и (5) следует, что (Qe)(x-s) = e (Qe)(x). (6). Пусть С = (Qe)(0). При Q = 0 соотношение (6) имеет вид Qe = Ce. ...
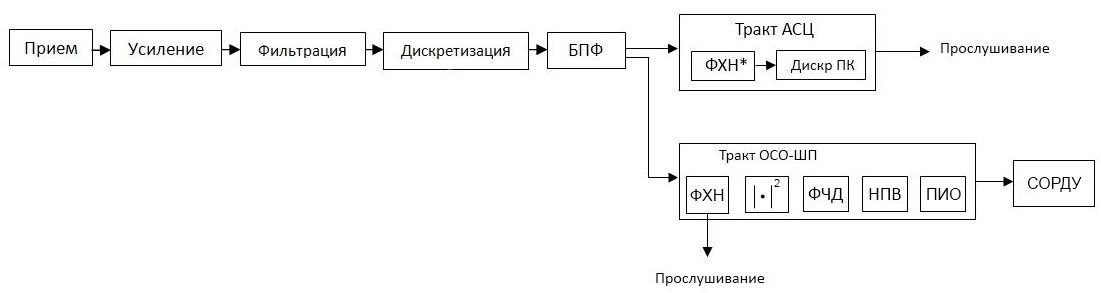
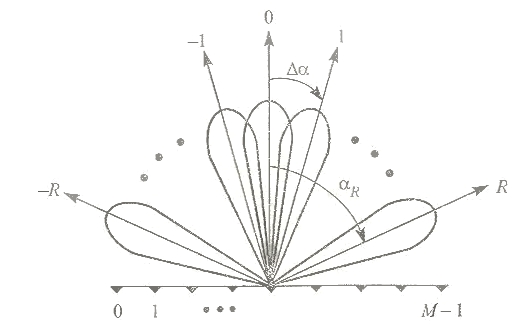
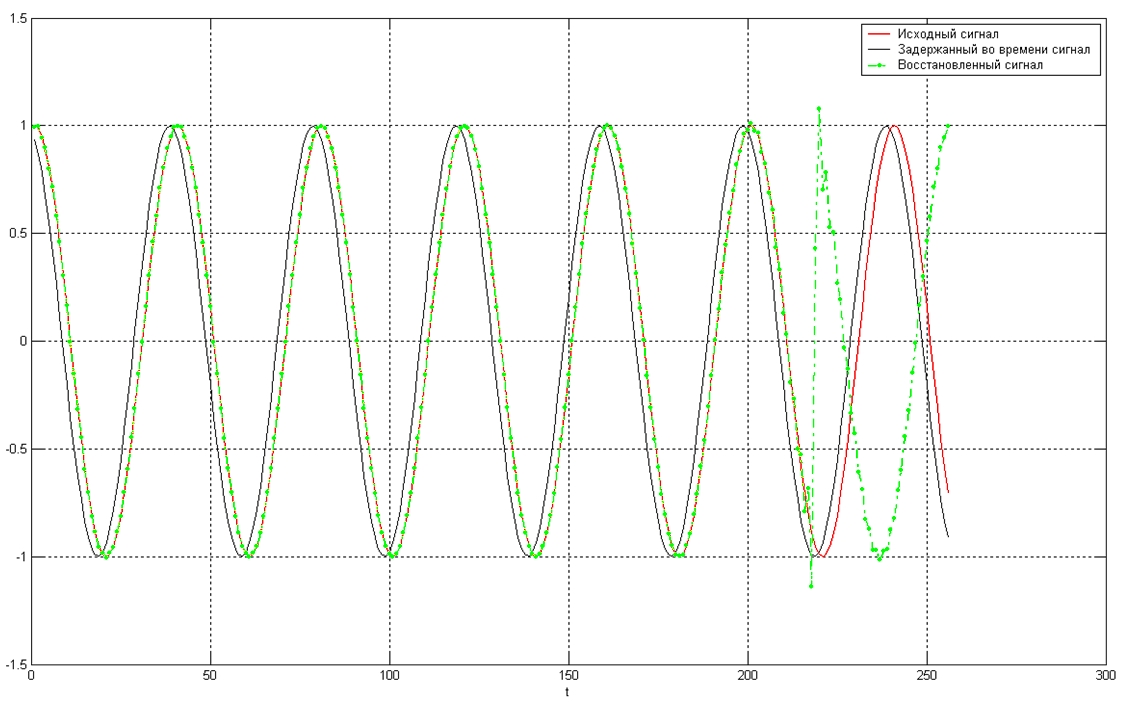
... частотного диапазона и внешний вид фильтра. То же самое мы видим и для других Частотных диапазонов на плакатах 2 и 3 . Доклад окончен Тема: Модель тракта прослушивания гидроакустических сигналов ОглавлениеВведение Место тракта прослушивания в структуре режима ШП типовой ГАС Формирование канала наблюдения в частотной области 3 Факторы, влияющие на восстановление сигнала 3.1 Перекрытие входных ...
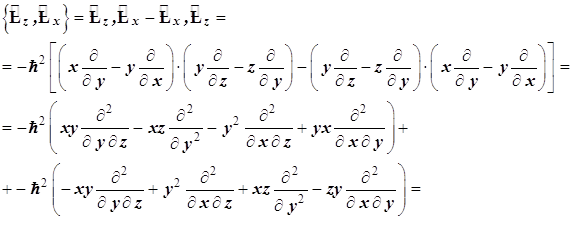
0 комментариев