Содержание
Введение
1.Кривые второго порядка
1.1 Эллипс
1.2 Гипербола
1.3 Парабола
2.Теоремы, связанные с кривыми второго порядка
Литература
Введение
Впервые кривые второго порядка изучались одним из учеников Платона. Его работа заключалась в следующем: если взять две пересекающиеся прямые и вращать их вокруг биссектрисы угла, ими образованного, то получится конусная поверхность. Если же пересечь эту поверхность плоскостью, то в сечении получаются различные геометрические фигуры, а именно эллипс, окружность, парабола, гипербола и несколько вырожденных фигур.
Однако эти научные знания нашли применение лишь в XVII, когда стало известно, что планеты движутся по эллиптическим траекториям, а пушечный снаряд летит по параболической. Ещё позже стало известно, что если придать телу первую космическую скорость, то оно будет двигаться по окружности вокруг Земли, при увеличении этой скорости — по эллипсу, а по достижении второй космической скорости тело по параболе покинет поле притяжения Земли.
1. Кривые второго порядка
Кривой 2-го порядка называется линия на плоскости, которая в некоторой декартовой системе координат определяется уравнением
ax2 + 2bxy + cy2 + 2dx + 2ey + f = 0
где a, b, c, d, e, f — вещественные коэффициенты, причем a2 + b2 + c2 ≠ 0 .
Вид кривой зависит от четырёх инвариантов:
инварианты относительно поворота и сдвига системы координат:

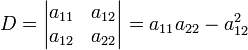
![]()
инвариант относительно поворота системы координат (полуинвариант):
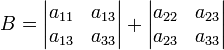
Многие важные свойства кривых второго порядка могут быть изучены при помощи характеристической квадратичной формы, соответствующей уравнению кривой:
![]()
Так, например, невырожденная кривая![]() оказывается вещественным эллипсом, мнимым эллипсом, гиперболой или параболой в зависимости от того, будет ли
оказывается вещественным эллипсом, мнимым эллипсом, гиперболой или параболой в зависимости от того, будет ли![]() положительно определённой, отрицательно определённой, неопределённой или полуопределённой квадратичной формой, что устанавливается по корням характеристического уравнения:
положительно определённой, отрицательно определённой, неопределённой или полуопределённой квадратичной формой, что устанавливается по корням характеристического уравнения:
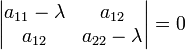
Или
λ2 − Iλ + D = 0.
Корни этого уравнения являются собственными значениями вещественной симметричной матрицы и, как следствие этого, всегда вещественны:
![]()
Кривые второго порядка классифицируются на невырожденные кривые и вырожденные.
Доказано, что кривая 2–го порядка, определяемая этим уравнением принадлежит к одному из следующих типов: эллипс, гипербола, парабола, пара прямых (пересекающихся, параллельных или совпадающих), точка, пустое множество.
Иными словами, для каждой кривой 2-го порядка (для каждого уравнения) существует такая система координат, в которой уравнение кривой имеет вид:
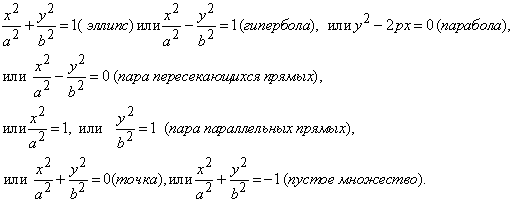
1.1 Эллипс
Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами эллипса, есть величина постоянная. Отрезки, соединяющие точку эллипса с фокусами, называются фокальными радиусами точки.
Если эллипс описывается каноническим уравнением
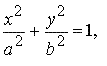
где a > 0 , b > 0, a > b > 0 — большая и малая полуоси эллипса, то фокусы эллипса расположены симметрично на оси абсцисс и имеют координаты (−c, 0) и ( c, 0), где
![]()
Величина e = c/a называется эксцентриситетом эллипса.
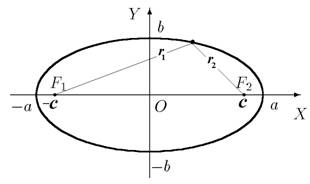
По определению эллипса r1 + r2 = 2a, r1 и r2 − фокальные радиусы, их длины вычисляются по формулам
![]()
Если фокусы эллипса совпадают, то эллипс является окружностью.
1.2 Гипербола
Гиперболой называется кривая второго порядка, которая в некоторой декартовой системе координат описывается уравнением
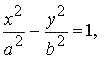
где a > 0, b > 0 — параметры гиперболы.
Это уравнение называется каноническим уравнением гиперболы, а система координат, в которой гипербола описывается каноническим уравнением, называется канонической.
В канонической системе оси координат являются осями симметрии гиперболы, а начало координат — ее центром симметрии.
Точки пересечения гиперболы с осью OX ( ± a, 0) называются вершинами гиперболы.
С осью OY гипербола не пересекается.
Отрезки a и b называются полуосями гиперболы.
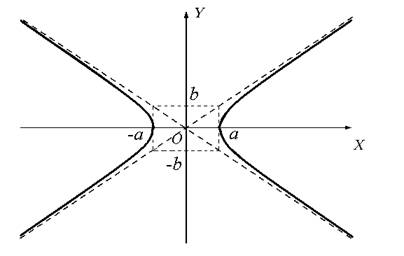
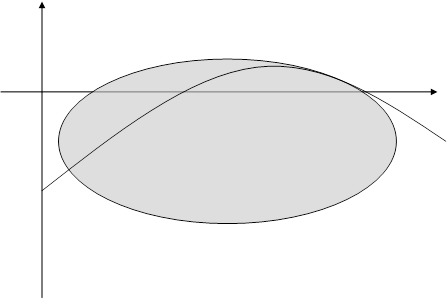
Рис.1
Прямые ay − bx = 0 и ay + bx = 0 — асимптоты гиперболы, при удалении точки гиперблы в бесконечность, соответствующая ветвь гиперболы приближается к одной из асимптот.
Уравнение описывает гиперболу, вершины которой лежат на оси OY в точках (0, ± b).
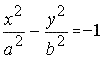
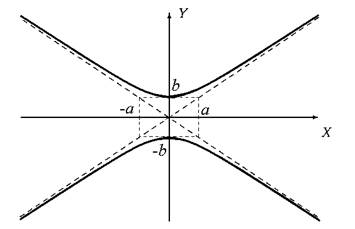
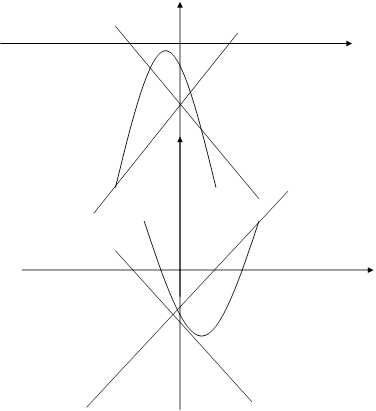
Рис.2
Такая гипербола называется сопряженной к гиперболе её асимптоты — те прямые ay − bx = 0 и ay + bx = 0. Говорят о паре сопряжённых гипербол.
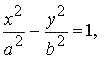
1.3 Парабола
Параболой называется кривая второго порядка, которая в некоторой декартовой системе координат описывается уравнением
y2 = 2 px
где p > 0 — параметр параболы.
Такое уравнение называется каноническим уравнением параболы, а система координат, в которой парабола описывается каноническим уравнением, называется канонической.
В канонической системе ось абсцисс является осью симметрии параболы, а начало координат — её вершиной.
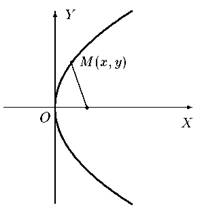
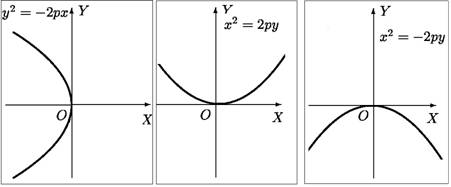
Рис.3
Уравнения y2 = −2 px, x2 = 2 py, и x2 = −2 py, p > 0, в той же самой канонической системе координат также описывают параболы:
2. Теоремы, связанные с кривыми второго порядка
Теоремма Паскамля — теорема проективной геометрии, которая гласит, что:
Если шестиугольник вписан в окружность либо любое другое коническое сечение (эллипс, параболу, гиперболу, даже пару прямых), то точки пересечения трёх пар противоположных сторон лежат на одной прямой. Теорема Паскаля двойственна к теореме Брианшона.
Теорема Брианшона является классической теоремой проективной геометрии. Она сформулируется следующим образом:
Если шестиугольник описан около конического сечения, то три диагонали, соединяющие противоположные вершины этого шестиугольника, проходят через одну точку.
В частности, в вырожденном случае:
Если стороны шестиугольника проходят поочерёдно через две данные точки, то три диагонали, соединяющие его противоположные вершины, проходят через одну точку.
Теорема Брианшона двойственна к теореме Паскаля, а её вырожденный случай двойственен к теореме Паппа.
Литература
1. Корн Г., Корн Т. Кривые второго порядка (конические сечения) // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 64-69.
2. Корн Г., Корн Т. 2.4-5. Характеристическая квадратичная форма и характеристическое уравнение // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 64.
3. В.А. Ильин, Э.Г. Позняк. Аналитическая геометрия, гл. 6. М.: "Наука", 1988.
Похожие работы
... Гипербола Две пересекающиеся прямые Гипербола II. Переход от общего уравнения кривой к каноническому Рассмотрим теперь случай, когда, и исследуем данное уравнение кривой второго порядка с помощью инвариантов. Из вышеприведенной таблицы видим, что при уравнение (1) определяет гиперболу и принимает вид: (2.1) Приведем уравнение кривой (2.1) к каноническому виду, ...
... третьего порядка. Яблонский А.И. [11, с.1752 - 1760] и Филипцов В.Ф. [9, с.469-476] изучали квадратичные системы с предположением, что частным интегралом являлись алгебраические кривые четвертого порядка. В данной работе рассматривается система (0.3) и проводится качественное исследование в целом системы (0.3) при условии, что частным интегралом является кривая четвертого порядка, которая ...
... форма j(х) = хТАх была отрицательно определенной, необходимо и достаточно, чтобы ее главные миноры четного порядка были положительны, а нечетного – отрицательны, то есть: М1 < 0, M2 > 0, М3 < 0, …, (–1)n Mn > 0. Пример 3. При каких значениях а и в квадратичная форма будет положительно определенной? j (х1, х2, x3) = Решение. Построим матрицу А и найдем ее главные миноры. ...
... кривой второго порядка и приведя его к каноническому виду, мы установили, что данная кривая — эллипс. Мы получили каноническое уравнение гиперболы при помощи преобразований параллельного переноса и поворота координатных осей. Исследование формы поверхности второго порядка Теоретическая часть Поверхностью второго порядка S называется геометрическое место точек, декартовы прямоугольные ...


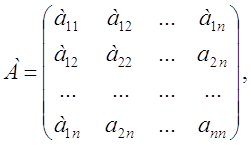
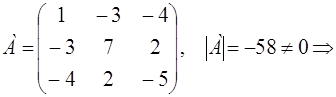
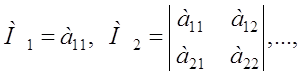
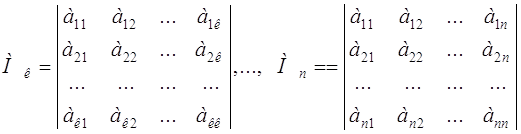
0 комментариев