Навигация
Модели принятия решения, с помощью которых можно оценить процесс преобразования входов в выходы или осуществить выбор вариантов
10. Модели принятия решения, с помощью которых можно оценить процесс преобразования входов в выходы или осуществить выбор вариантов.
Действия и решения в системе являются прерогативой ЛПР. Каждое решение должно направлять систему на достижение поставленных целей.
Существует два типа моделей принятия решений:
модели преобразования, связывающие вход и выход системы;
модели выбора, позволяющие выбрать наилучший вариант системы для достижения цели, из некоторого исходного множества вариантов.
В нашем случае используем модель второго типа - модель выбора, для чего составим сравнительную таблицу с учётом важности характеристик (критериев). В качестве модели выбора используем аддитивную свёртку.
Таблица 1.
| Характеристики (критерии) | Марки кухонных комбайнов (варианты) | ||
| В1 | В2 | В3 | |
| Braun CombiMax K700 Vital | Bosch MCM 210 | Moulinex FP 6021 Twin System | |
| К1- количество выполняемых функций | 23 | 17 | 34 |
| К2- количество приспособлений | 15 | 11 | 21 |
| К3- количество скоростных режимов | 2 | 2 | 2 |
| К4- мощность (Ватт) | 600 | 450 | 700 |
| К5- стоимость (руб) | 4 198 | 3 380 | 3 890 |
| К6- гарантия | 3 года | 2 года | 5 лет |
Оценим каждую альтернативу (вариант) множеством критериев.
Альтернативы:
В1 - Braun CombiMax K700 Vital.
В2 - Bosch MCM 210.
В3 - Moulinex FP 6021 Twin System.
Оценка:
К1 - В3 > В1 > В2
К2 - В3 > В1 > В2
К3 - В1 = В2 = В3
К4 - В3 > В1 > В2
К5 - В1 > В3 > В2
К6 - В3 > В1 > В2
Проведём попарное сравнение критериев по важности по девятибалльной шкале, и составим матрицу (таблица 2) размера (6 x 6):
равная важность - 1,умеренное превосходство - 3,значительное превосходство - 5,сильное превосходство - 7,очень сильное превосходство - 9,в промежуточных случаях ставятся чётные оценки - 2, 4, 6,8.
Таблица 2.
| Критерии | К1 | К2 | К3 | К4 | К5 | К6 | НВП |
| К1 | 1 | 1 | 4 | 7 | 4 | 6 | 0,367 |
| К2 | 1 | 1 | 5 | 5 | 3 | 4 | 0,321 |
| К3 | 1/4 | 1/5 | 1 | 3 | 3 | 2 | 0,122 |
| К4 | 1/7 | 1/5 | 1/3 | 1 | 2 | 2 | 0,072 |
| К5 | 1/4 | 1/3 | 1/3 | 1/2 | 1 | 1 | 0,061 |
| К6 | 1/6 | 1/4 | 1/2 | 1/2 | 1 | 1 | 0,058 |
| λ max = 6,3478 ИС = 0,0696 ОС = 0,0561 | |||||||
Нормализованный вектор приоритетов (НВП) определяется по следующей схеме:
а) рассчитывается среднее геометрическое элементов в каждой строке матрицы по формуле:
![]()
б) рассчитывается сумма средних геометрических:
∑= а1 + а2 + … + аn
в) вычисляют компоненты НВП:
аn = аn / ∑.
Каждый компонент НВП представляет собой оценку важности соответствующего критерия.
Проверяется согласованность оценок в матрице. Для этого подсчитываются три характеристики:
а) собственное значение матрицы по формуле:
λ макс = ∑
элементов 1го столбца × 1й компонент НВП + ∑ элементов 2го столбца × 2й компонент НВП + … + ∑ элементов nго столбца × nй компонент НВП,
где × - знак умножения;
![]()
![]() случайной согласованности, определяемый теоретически для случая, когда оценки в матрице представлены случайным образом, и зависящий от размера матрицы. Значения ПСС представлены в таблице 3.
случайной согласованности, определяемый теоретически для случая, когда оценки в матрице представлены случайным образом, и зависящий от размера матрицы. Значения ПСС представлены в таблице 3.
Таблица 3.
| Размер матрицы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| ПСС | 0 | 0 | 0,58 | 0,90 | 1,12 | 1,24 | 1,32 | 1,41 | 1,45 | 1,49 |
Оценки в матрице считаются согласованными, если ОС ≤ 10÷15%.
Проведём попарное сравнение пригодности (ценности) вариантов по каждому критерию по той же шкале, что и для критериев. Для этого необходимо предварительно проранжировать варианты по каждому критерию. Затем полученные результаты занесём в таблицу (таблица 4). В каждом случае подсчитываются:
λimax; ИСi; ОСi.
Таблица 4.
| К1 | В1 | В2 | В3 | НВП | К2 | В1 | В2 | В3 | НВП | К3 | В1 | В2 | В3 | НВП |
| В1 | 1 | 3 | 1/5 | 0,188 | В1 | 1 | 3 | 1/5 | 0,188 | В1 | 1 | 1 | 1 | 0,333 |
| В2 | 1/3 | 1 | 1/7 | 0,081 | В2 | 1/3 | 1 | 1/7 | 0,081 | В2 | 1 | 1 | 1 | 0,333 |
| В3 | 5 | 7 | 1 | 0,731 | В3 | 5 | 7 | 1 | 0,731 | В3 | 1 | 1 | 1 | 0,333 |
| λ 1 max = 3,0649 ИС1 = 0,0324 ОС1 = 0,0559 | λ 2max = 3,0649 ИС2 = 0,0324 ОС2 = 0,0559 | λ 3 max = 3,0000 ИС3 = 0,0000 ОС3 = 0,0000 | ||||||||||||
| К4 | В1 | В2 | В3 | НВП | К5 | В1 | В2 | В3 | НВП | К6 | В1 | В2 | В3 | НВП |
| В1 | 1 | 3 | 1/3 | 0,258 | В1 | 1 | 7 | 3 | 0,649 | В1 | 1 | 3 | 1/5 | 0,188 |
| В2 | 1/3 | 1 | 1/5 | 0,105 | В2 | 1/ | 1 | 1/5 | 0,072 | В2 | 1/3 | 1 | 1/7 | 0,081 |
| В3 | 3 | 5 | 1 | 0,637 | В3 | 1/3 | 5 | 1 | 0,279 | В3 | 5 | 7 | 1 | 0,731 |
| λ 4 max = 3,0385 ИС4 = 0,0193 ОС4 = 0,0332 | λ 5 max = 3,0649 ИС5 = 0,0324 ОС5 = 0,0559 | λ 6 max = 3,0649 ИС6 = 0,0324 ОС6 = 0,0559 | ||||||||||||
Далее необходимо подсчитать значение общего критерия для альтернативы хЄХ, показывающий её пригодность для достижения цели для каждого варианта по формуле аддитивной свёртки:
![]()
![]()
аj - относительный вес (важность) частного критерия Kj.
Таблица 5.
| аjKj | варианты | ||
| В1 | В2 | В3 | |
| а1К1 | 0,367Í0,188 = 0,0689 | 0,367Í0,081 = 0,0297 | 0,367Í0,731 = 0,2682 |
| а2К2 | 0,321Í0,188 = 0,0603 | 0,321Í0,081 = 0,0260 | 0,321Í0,731 = 0,2346 |
| а3К3 | 0,122Í0,333 = 0,0406 | 0,122Í0,333 = 0,0406 | 0,122Í0,333 = 0,0406 |
| а4К4 | 0,072Í0,258 = 0,0185 | 0,072Í0,105 = 0,0075 | 0,072Í0,637 = 0,0458 |
| а5К5 | 0,061Í0,649 = 0,0395 | 0,061Í0,072 = 0,0043 | 0,061Í0,279 = 0,0170 |
| а6К6 | 0,058Í0,188 = 0,0109 | 0,058Í0,081 = 0,0046 | 0,058Í0,731 = 0,0423 |
|
|
|
| |
Для весов выполняется условие нормировки ![]() , которое необходимо, чтобы результаты, полученные в разных условиях, были сопоставимы.
, которое необходимо, чтобы результаты, полученные в разных условиях, были сопоставимы.
В нашем случае:
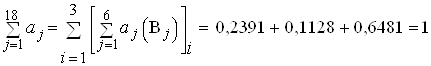 ,
,
то есть условие нормировки выполняется.
Наилучшее решение определяем по выражению:
![]()
К (х) - одна из свёрток выбираемых ЛПР, в нашем случае аддитивная свёртка.
Итак, по расчётам видно, что наибольшее значение критерия имеет третий вариант (0,6481), который является предпочтительным перед остальными.
И в заключении необходимо проверить достоверность решения, для чего подсчитываются:
обобщённый индекс согласования (ОИС),
обобщённый показатель случайной согласованности (ОПСС),
обобщённое отношение согласованности (ООС).
1. ОИС подсчитывается по следующей формуле:
ОИС = ИС1 Í НВП (К1) + ИС2 Í НВП (К2) + … + ИС6 Í НВП (К6)
При этом:
ИСi берётся из таблицы 4.
НВП (Кj) берётся из таблицы 2.
ОИС = 0,0324 Í 0,367 + 0,0324 Í 0,321 + 0,0000 Í 0,122 + 0,0193 Í 0,072 + 0,0324 Í 0,061 + 0,0324 Í 0,058 = 0,0119 + 0,0104 + 0 + 0,0014 + 0,0019 + 0,0019 = 0,0275
2. ОПСС подсчитывается так же как и ОИС, с той разницей, что вместо ИС1, ИС2 и так далее из таблицы 3 подставляются ПСС, соответствующие размеру матриц сравнения вариантов из таблицы 3. В данном случае размер матрицы 3, поэтому ПСС = 0,58.
ОПСС = 0,58 Í 0,367 + 0,58 Í 0,321 + 0,58 Í 0,122 + 0,58 Í 0,072 + 0,58 Í 0,061 + 0,58 Í 0,058 = 0,21286 + 0,18618 + 0,07076 + 0,04176 + 0,03538 + 0,03364 = 0,58
3. ООС рассчитывается по следующей формуле:
![]()
Решение считается достоверным, если
ООС ≤ 10 ÷ 15%.
![]()
ООС удовлетворяет условию, а значит, решение является достоверным.
11. Тип системы.
Кухонный комбайн является физической, технической, искусственной неживой, статической, дискретной, относительно закрытой системой. По преобразовательным возможностям относится ко второму типу (изменяются отдельные характеристики входного элемента).
12. Свойства системы. В чём они состоят?
Система "кухонный комбайн" является иерархически упорядоченной, так как состоит из подсистем.
Система централизована, так как центром является мотор, обеспечивающий работу (движение) остальных элементов кухонного комбайна.
Система является инерционной, так как имеет конечное время переработки.
Система адаптивна, так как сохраняет свои функции при возмущающих воздействиях среды, например, при изменении качества ухода и обслуживания, изменении погодных условий (температура, влажность, давление), и т.д.
Похожие работы
... , телеология, теория информации, инженерная теория связи, теория ЭВМ, системотехника, исследование операций и сопряженные с ними научные и инженерные направления. [5] Философские категории, используемые в системном анализе Акофф и Эмери пишут: Кибернетики дают цели и информации такие определения, которые как нельзя лучше приспособлены для исследований, проводимых самими кибернетиками. Затем ...
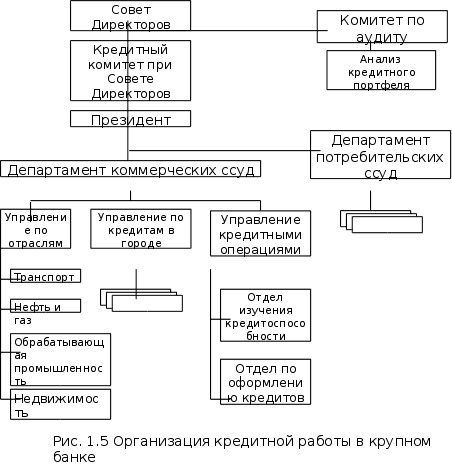
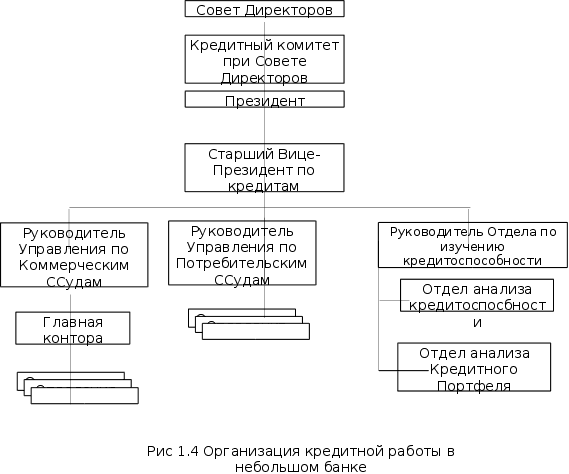
... выявления недостатков и «узких мест» этих систем и подготовке рекомендаций по улучшению функционирования и прогнозированию их развития в условиях информационной неопределенности. Глава 3 Системный анализ управления кредитами.3.1. Анализ кредитных задолженностей в 1995 и 1996 годах. Работа банковской системы любого государства определяется, прежде всего, конечными результатами, представленными в ...
... системы. Главные особенности системного подхода – динамичность, взаимодействие, взаимозависимость и взаимосвязь элементов системы, комплексность, целостность, соподчинённость, выделение ведущего звена. Системный подход в экономическом анализе позволяет разработать научно обоснованные варианты решения хозяйственных задач, определить эффективность этих вариантов, что даёт основание для выбора ...
... , динамические и статические, простые и сложные, естественные и искусственные, с управлением и без управления, непрерывные и дискретные, детерминированные и стохастические, открытые и замкнутые. Основы системного анализа Деление систем на физические и абстрактные позволяет различать реальные системы (объекты, явления, процессы) и системы, являющиеся определенными отображениями (моделями) ре ...


0 комментариев