Навигация
Расстояние Хемминга (p = 1)
1. Расстояние Хемминга (p = 1).
![]()
dxeм (В1) = 0,293 |0,714-0,714| + 0,251 |0,105-0,637| + 0,170 |0,333-0,333| +
+ 0,116 |0,114-0,481| + 0,077 |0,114-0,481| + 0,039 |0,637-0,637| +
+ 0,037 |0,114-0,481| + 0,017 |0,111-0,778| =
= 0 + 0,1335 + 0 + 0,0425 + 0,0282 + 0 + 0,0135 + 0,0113 = 0,2290
dxeм (В2) = 0,293 |0,143-0,714| + 0,251 |0,637-0,637| + 0,170 |0,333-0,333| +
+ 0,116 |0,405-0,481| + 0,077 |0,405-0,481| + 0,039 |0,105-0,637| +
+ 0,037 |0,405-0,481| + 0,017 |0,778-0,778| =
= 0,1673 + 0 + 0 + 0,0088 + 0,0058 + 0,0207 + 0,0028 + 0 = 0, 2054
dxeм (В3) = 0,293 |0,143-0,714| + 0,251 |0,258-0,637| + 0,170 |0,333-0,333| +
+ 0,116 |0,481-0,481| + 0,077 |0,481-0,481| + 0,039 |0,258-0,637| +
+ 0,037 |0,481-0,481| + 0,017 |0,111-0,778| =
= 0,1673 + 0,0951 + 0 + 0 + 0 + 0,0147 + 0 + 0,0113 = 0,2884
dxeм (В1) = 0,2290
dxeм (В2) = 0, 2054
dxeм (В3) = 0,2884
Наилучшим является второй вариант (В2), так как ему соответствует наименьшее значение меры (0, 2054).
1. Расстояние Евклида (p = 2).
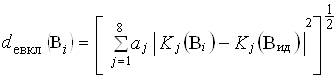
dевкл (В1) = [0,293 |0,714 - 0,714|2 + 0,251 |0,105 - 0,637|2 +
+ 0,170 |0,333 - 0,333|2 + 0,116 |0,114 - 0,481|2 +
+ 0,077 |0,114 - 0,481|2 + 0,039 |0,637 - 0,637|2 +
+ 0,037 |0,114 - 0,481|2 + 0,017 |0,111 - 0,778|2] 1/2 =
= [0+0,0178+0+0,0018+0,0007+0+0,0001+0,0001] 1/2= [0,0205] 1/2= 0,1431
dевкл (В2) = [0,293 |0,143 - 0,714|2 + 0,251 |0,637 - 0,637|2 +
+ 0,170 |0,333 - 0,333|2 + 0,116 |0,405 - 0,481|2 +
+ 0,077 |0,405 - 0,481|2 + 0,039 |0,105 - 0,637|2 +
+ 0,037 |0,405 - 0,481|2 + 0,017 |0,778 - 0,778|2] 1/2 =
= [0,0279+0+0+0,0001+0,0001+0,0004+0,0001+0] 1/2= [0,0286] 1/2= 0,1691
dевкл (В3) = [0,293 |0,143 - 0,714|2 + 0,251 |0,258 - 0,637|2 +
+ 0,170 |0,333 - 0,333|2 + 0,116 |0,481 - 0,481|2 +
+ 0,077 |0,481 - 0,481|2 + 0,039 |0,258 - 0,637|2 +
+ 0,037 |0,481 - 0,481|2 + 0,017 |0,111 - 0,778|2] 1/2 =
= [0,0279+0,0090+0+0+0+0,0002+0+0,0001] 1/2 = [0,0372] 1/2 = 0, 1928
Наилучшим является первый вариант (В1), так как ему соответствует наименьшее значение меры (0,1431).
3. Расстояние по максимальному различию (p = ∞).
В данном случае берётся максимальное различие между критериями по формуле:
![]()
dxeм (В1) = 0,251 |0,105-0,637| = 0,1335
dxeм (В2) = 0,293 |0,143-0,714| = 0,1673
dxeм (В3) = 0,293 |0,143-0,714| = 0,1673
Наилучшим является первый вариант (В1), так как ему соответствует наименьшее значение меры (0,1135).
4. Расстояние по минимальному различию (p = - ∞).
В данном случае берётся минимальное различие между критериями по формуле:
![]()
dxeм (В1) = 0,293 |0,714 - 0,714| = 0
dxeм (В2) = 0,251 |0,637 - 0,637| = 0
dxeм (В3) = 0,116 |0,481 - 0,481| = 0
С учётом числа и веса критериев наилучшим является первый вариант (В1).
Вывод.
После произведённых расчётов было выявлено что:
вариант В1 - частная фирма является предпочтительным по следующим методам:
методу главного критерия,
по свёртке по наилучшему критерию,
по аддитивной свёртке,
по методу расстояния при р = 2, p = ∞, p = - ∞;
вариант В2 - государственное предприятие является предпочтительным по следующим методам:
по свёртке по наихудшему критерию с учётом важности критериев,
по мультипликативной свёртке,
по методу расстояния при р = 1;
вариант В3 - учебный институт является предпочтительным по:
свёртке по наихудшему критерию без учёта важности критериев.
Но поскольку в при решении задачи была применена аддитивная свёртка (плавное убывание весов критериев), то наилучшим вариантом следует считать вариант В1 - частная фирма, полученный по этой свёртке.
Задача № 6
Условие задачи.
По результатам опроса экспертов составлена таблица оценок m вариантов решения некоторой проблемы по n критериям. Использованы балльные оценки по пятибалльной шкале и словесные оценки, причём большей оценке соответствует лучшее значение критерия.
Таблица 1.
| Варианты решения | Значения критериев | |||||||||
| К1 | К2 | К3 | К4 | К5 | К6 | К7 | К8 | К9 | К10 | |
| В1 | 2 | Н | 2 | 3 | С | 2 | 3 | 4 | 4 | В |
| В2 | 4 | ОВ | 3 | 3 | С | 5 | 4 | 4 | 4 | В |
| В3 | 3 | В | 3 | 2 | Н | 4 | 3 | 2 | 1 | С |
| В4 | 4 | ОВ | 3 | 3 | Н | 5 | 4 | 3 | 4 | В |
| В5 | 1 | С | 3 | 2 | ОН | 3 | 2 | 4 | 2 | Н |
| В6 | 5 | В | 4 | 4 | С | 4 | 5 | 4 | 4 | В |
| В7 | 4 | В | 4 | 4 | ОН | 3 | 4 | 2 | 3 | С |
| В8 | 3 | ОН | 4 | 3 | С | 4 | 3 | 3 | 2 | С |
| В9 | 4 | В | 4 | 3 | В | 3 | 4 | 4 | 4 | В |
| В10 | 5 | ОВ | 4 | 3 | В | 4 | 5 | 4 | 4 | ОВ |
| В11 | 3 | С | 2 | 2 | С | 3 | 4 | 3 | 1 | В |
| В12 | 2 | В | 3 | 3 | В | 4 | 4 | 4 | 4 | С |
| В13 | 5 | В | 4 | 3 | В | 4 | 5 | 4 | 4 | ОВ |
| В14 | 4 | ОВ | 4 | 4 | В | 4 | 5 | 4 | 4 | ОВ |
| В15 | 3 | С | 4 | 4 | В | 4 | 5 | 4 | 4 | С |
По данным таблицы, считая все критерии одинаково важными, требуется:
выделить множество Парето-решений;
представить результаты сравнения оставшихся вариантов в виде диаграммы в полярных координатах (каждая координата - отдельный критерий);
используя диаграмму, определить, какой вариант решения является предпочтительным;
проверить результаты выбора, используя подходящую свёртку критериев;
оценить ошибку выбора, при условии, что ошибка оценок таблицы составляет (0,1 + 0,1 x i).
Для получения варианта задания следует вычеркнуть из исходной таблицы i-й столбец и i-ю строку, а также j-й столбец и j-ю строку (оставшиеся строки и столбцы не перенумеровываются).
Данные для решения задачи.
Таблица 2.
| Варианты решения | Значения критериев | |||||||
| К1 | К2 | К4 | К5 | К6 | К7 | К8 | К10 | |
| В1 | 2 | Н | 3 | С | 2 | 3 | 4 | В |
| В2 | 4 | ОВ | 3 | С | 5 | 4 | 4 | В |
| В4 | 4 | ОВ | 3 | Н | 5 | 4 | 3 | В |
| В5 | 1 | С | 2 | ОН | 3 | 2 | 4 | Н |
| В6 | 5 | В | 4 | С | 4 | 5 | 4 | В |
| В7 | 4 | В | 4 | ОН | 3 | 4 | 2 | С |
| В8 | 3 | ОН | 3 | С | 4 | 3 | 3 | С |
| В10 | 5 | ОВ | 3 | В | 4 | 5 | 4 | ОВ |
| В11 | 3 | С | 2 | С | 3 | 4 | 3 | В |
| В12 | 2 | В | 3 | В | 4 | 4 | 4 | С |
| В13 | 5 | В | 3 | В | 4 | 5 | 4 | ОВ |
| В14 | 4 | ОВ | 4 | В | 4 | 5 | 4 | ОВ |
| В15 | 3 | С | 4 | В | 4 | 5 | 4 | С |
Словесные оценки, используемые в таблице:
ОВ - очень высокое значение (5),
В - высокое значение (4),
С - среднее значение (3),
Н - низкое значение (2),
ОН - очень низкое значение (1).
Решение.
Множество Парето-решений.
Множество Парето состоит из вариантов решений, которые по всем критериям не хуже остальных и хотя бы по одному критерию лучше остальных. Построение множества Парето происходит путём попарного сравнения альтернатив. Альтернативы из него называются Парето-решениями.
Итак, пользуясь данными таблицы 2, выделим множество Парето-решений в попарном сравнении вариантов, начиная с варианта В1, то есть сравним его с вариантами В2, В4 и так далее. Для этого составим сравнительные таблицы, которые можно считать единой таблицей (таблица 3).
Таблица 3.
В1 и В2 → В1 - отбросить
| Варианты решения | Значения критериев | |||||||
| К1 | К2 | К4 | К5 | К6 | К7 | К8 | К10 | |
| В1 | 2 | Н | 3 | С | 2 | 3 | 4 | В |
| В2 | 4+ | ОВ+ | 3 | С | 5+ | 4+ | 4 | В |
В2 и В4 → В4 - отбросить
| Варианты решения | Значения критериев | |||||||
| К1 | К2 | К4 | К5 | К6 | К7 | К8 | К10 | |
| В2 | 4 | ОВ | 3 | С+ | 5 | 4 | 4+ | В |
| В4 | 4 | ОВ | 3 | Н | 5 | 4 | 3 | В |
В2 и В5 → В5 - отбросить
| Варианты решения | Значения критериев | |||||||
| К1 | К2 | К4 | К5 | К6 | К7 | К8 | К10 | |
| В2 | 4+ | ОВ+ | 3+ | С+ | 5+ | 4+ | 4 | В+ |
| В5 | 1 | С | 2 | ОН | 3 | 2 | 4 | Н |
В2 и В6 → не сравнимы
| Варианты решения | Значения критериев | |||||||
| К1 | К2 | К4 | К5 | К6 | К7 | К8 | К10 | |
| В2 | 4 | ОВ+ | 3 | С | 5+ | 4 | 4 | В |
| В6 | 5+ | В | 4+ | С | 4 | 5+ | 4 | В |
В2 и В7 → не сравнимы
| Варианты решения | Значения критериев | |||||||
| К1 | К2 | К4 | К5 | К6 | К7 | К8 | К10 | |
| В2 | 4 | ОВ+ | 3 | С+ | 5+ | 4 | 4+ | В+ |
| В7 | 4 | В | 4+ | ОН | 3 | 4 | 2 | С |
В2 и В8 → В8 - отбросить
| Варианты решения | Значения критериев | |||||||
| К1 | К2 | К4 | К5 | К6 | К7 | К8 | К10 | |
| В2 | 4+ | ОВ+ | 3 | С | 5+ | 4+ | 4+ | В+ |
| В8 | 3 | ОН | 3 | С | 4 | 3 | 3 | С |
В2 и В10 → не сравнимы
| Варианты решения | Значения критериев | |||||||
| К1 | К2 | К4 | К5 | К6 | К7 | К8 | К10 | |
| В2 | 4 | ОВ | 3 | С | 5+ | 4 | 4 | В |
| В10 | 5+ | ОВ | 3 | В+ | 4 | 5+ | 4 | ОВ+ |
В2 и В11 → В11 - отбросить
| Варианты решения | Значения критериев | |||||||
| К1 | К2 | К4 | К5 | К6 | К7 | К8 | К10 | |
| В2 | 4+ | ОВ+ | 3+ | С | 5+ | 4 | 4+ | В |
| В11 | 3 | С | 2 | С | 3 | 4 | 3 | В |
В2 и В12 → не сравнимы
| Варианты решения | Значения критериев | |||||||
| К1 | К2 | К4 | К5 | К6 | К7 | К8 | К10 | |
| В2 | 4+ | ОВ+ | 3 | С | 5+ | 4 | 4 | В+ |
| В12 | 2 | В | 3 | В+ | 4 | 4 | 4 | С |
В2 и В13 → не сравнимы
| Варианты решения | Значения критериев | |||||||
| К1 | К2 | К4 | К5 | К6 | К7 | К8 | К10 | |
| В2 | 4 | ОВ+ | 3 | С | 5+ | 4 | 4 | В |
| В13 | 5+ | В | 3 | В+ | 4 | 5+ | 4 | ОВ+ |
В2 и В14 → не сравнимы
| Варианты решения | Значения критериев | |||||||
| К1 | К2 | К4 | К5 | К6 | К7 | К8 | К10 | |
| В2 | 4 | ОВ | 3 | С | 5+ | 4 | 4 | В |
| В14 | 4 | ОВ | 4+ | В+ | 4 | 5+ | 4 | ОВ+ |
В2 и В15 → не сравнимы
| Варианты решения | Значения критериев | |||||||
| К1 | К2 | К4 | К5 | К6 | К7 | К8 | К10 | |
| В2 | 4+ | ОВ+ | 3 | С | 5+ | 4 | 4 | В+ |
| В15 | 3 | С | 4+ | В+ | 4 | 5+ | 4 | С |
В6 и В7 → В7 отбросить
| Варианты решения | Значения критериев | |||||||
| К1 | К2 | К4 | К5 | К6 | К7 | К8 | К10 | |
| В6 | 5+ | В | 4 | С+ | 4+ | 5+ | 4+ | В+ |
| В7 | 4 | В | 4 | ОН | 3 | 4 | 2 | С |
В6 и В10 → не сравнимы
| Варианты решения | Значения критериев | |||||||
| К1 | К2 | К4 | К5 | К6 | К7 | К8 | К10 | |
| В6 | 5 | В | 4+ | С | 4 | 5 | 4 | В |
| В10 | 5 | ОВ+ | 3 | В+ | 4 | 5 | 4 | ОВ+ |
В6 и В12 → не сравнимы
| Варианты решения | Значения критериев | |||||||
| К1 | К2 | К4 | К5 | К6 | К7 | К8 | К10 | |
| В6 | 5+ | В | 4+ | С | 4 | 5+ | 4 | В+ |
| В12 | 2 | В | 3 | В+ | 4 | 4 | 4 | С |
В6 и В13 → не сравнимы
| Варианты решения | Значения критериев | |||||||
| К1 | К2 | К4 | К5 | К6 | К7 | К8 | К10 | |
| В6 | 5 | В | 4+ | С | 4 | 5 | 4 | В |
| В13 | 5 | В | 3 | В+ | 4 | 5 | 4 | ОВ+ |
В6 и В14 → не сравнимы
| Варианты решения | Значения критериев | |||||||
| К1 | К2 | К4 | К5 | К6 | К7 | К8 | К10 | |
| В6 | 5+ | В | 4 | С | 4 | 5 | 4 | В |
| В14 | 4 | ОВ+ | 4 | В+ | 4 | 5 | 4 | ОВ+ |
В6 и В15 → не сравнимы
| Варианты решения | Значения критериев | |||||||
| К1 | К2 | К4 | К5 | К6 | К7 | К8 | К10 | |
| В6 | 5+ | В+ | 4 | С | 4 | 5 | 4 | В+ |
| В15 | 3 | С | 4 | В+ | 4 | 5 | 4 | С |
В10 и В12 → В12 отбросить
| Варианты решения | Значения критериев | |||||||
| К1 | К2 | К4 | К5 | К6 | К7 | К8 | К10 | |
| В10 | 5+ | ОВ+ | 3 | В | 4 | 5+ | 4 | ОВ+ |
| В12 | 2 | В | 3 | В | 4 | 4 | 4 | С |
В10 и В13 → В13 отбросить
| Варианты решения | Значения критериев | |||||||
| К1 | К2 | К4 | К5 | К6 | К7 | К8 | К10 | |
| В10 | 5 | ОВ+ | 3 | В | 4 | 5 | 4 | ОВ |
| В13 | 5 | В | 3 | В | 4 | 5 | 4 | ОВ |
В10 и В14 → не сравнимы
| Варианты решения | Значения критериев | |||||||
| К1 | К2 | К4 | К5 | К6 | К7 | К8 | К10 | |
| В10 | 5+ | ОВ | 3 | В | 4 | 5 | 4 | ОВ |
| В14 | 4 | ОВ | 4+ | В | 4 | 5 | 4 | ОВ |
В10 и В15 → не сравнимы
| Варианты решения | Значения критериев | |||||||
| К1 | К2 | К4 | К5 | К6 | К7 | К8 | К10 | |
| В10 | 5+ | ОВ+ | 3 | В | 4 | 5 | 4 | ОВ+ |
| В15 | 3 | С | 4+ | В | 4 | 5 | 4 | С |
В14 и В15 → В15 отбросить
| Варианты решения | Значения критериев | |||||||
| К1 | К2 | К4 | К5 | К6 | К7 | К8 | К10 | |
| В14 | 4+ | ОВ+ | 4 | В | 4 | 5 | 4 | ОВ+ |
| В15 | 3 | С | 4 | В | 4 | 5 | 4 | С |
После завершения процедуры сравнения у нас образовалось множество Парето, которое состоит из вариантов В2, В6, В10 и В14. Остальные варианты исключены из дальнейшего рассмотрения.
В окончательном виде данное множество Парето имеет следующий вид:
π = { В2, В6, В10, В14}
Результаты сравнения оставшихся вариантов в виде диаграммы в полярных координатах.
Между собой варианты В2, В6, В10 и В14 не сравнимы, но нам необходимо выбрать наилучшее решение. Для этого применим один из графических методов - метод диаграмм. Для чего построим диаграмму в полярных координатах. Значения (оценки) критериев по данным вариантам берём из таблицы 3.
Таблица 3.
| Варианты решения | Значения критериев | |||||||
| К1 | К2 | К4 | К5 | К6 | К7 | К8 | К10 | |
| В2 | 4 | ОВ | 3 | С | 5 | 4 | 4 | В |
| В6 | 5 | В | 4 | С | 4 | 5 | 4 | В |
| В10 | 5 | ОВ | 3 | В | 4 | 5 | 4 | ОВ |
| В14 | 4 | ОВ | 4 | В | 4 | 5 | 4 | ОВ |
ОВ - очень высокое значение (5)
В - высокое значение (4)
С - среднее значение (3)
 К1
К1
К10 К2
К8 К4
К7 К5
К6
В2 В10
В6 В14
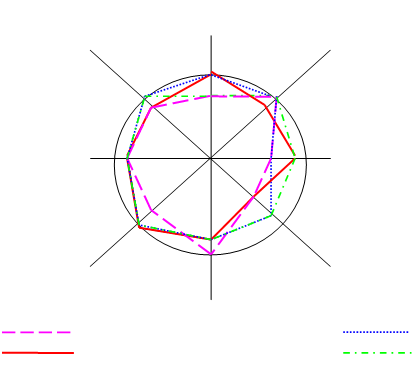
Рис. 1. Диаграмма сравнения вариантов В2,В6, В10 и В14.
Определение предпочтительного варианта по диаграмме. Глядя на диаграмму сравнения, можно с уверенностью сказать, что площади многоугольников, соответствующих вариантам В10 и В14 заметно больше площадей многоугольников, соответствующих вариантам В2 и В6. Следовательно, варианты В10 и В14 являются предпочтительными, то есть наилучшими.
Проверка результатов выбора. Для проверки результатов выбора используем аддитивную свёртку. Так как по условию задачи все критерии считаются одинаково важными, то общий критерий равен среднему значений частных критериев для каждого варианта. Подсчитаем для каждого из оставшихся вариантов величину.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
По расчётам видно, что наибольшее значение общего критерия имеют варианты В10 и В14, то есть, они являются предпочтительными, что совпадает с результатами, полученными по диаграмме.
Оценка ошибки выбора. Метод диаграмм - это приближённый метод, что является его преимуществом, так как позволяет нивелировать (сгладить) ошибки в оценках вариантов по критериям, приведённых в таблице 1. На этом этапе мы и подсчитаем ошибку выбора.
Среднеквадратическая ошибка определения общего критерия составляет:
![]() , где
, где
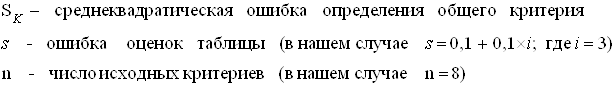
Доверительная ошибка (при вероятности Р = 0,95) равна:
![]()
Произведём расчёты.
![]()
![]()
Сравним результаты.
![]()
![]()
Поскольку после подсчётов мы видим, что ![]() , то это означает что варианты (В10 и В14) и (В2 и В6) значительно различаются. Этим мы подтвердили все предыдущие расчёты. Также мы видим, что
, то это означает что варианты (В10 и В14) и (В2 и В6) значительно различаются. Этим мы подтвердили все предыдущие расчёты. Также мы видим, что
![]() ,
,
то есть варианты В10 и В14 являются равноценными.
Ответ: варианты В10 и В14 являются равноценными, остальные варианты можно отбросить.
Библиография
1. Романов В.Н. Техника анализа сложных систем. - СПб.: СЗТУ - 2007. - 227 с.
2. Романов В.Н. Основы системного анализа: учебно-методический комплекс. - СПб.: СЗТУ, 2008. - 254 с.
3. Лекции по дисциплине "Системный анализ в управлении предприятием".
Похожие работы
... , телеология, теория информации, инженерная теория связи, теория ЭВМ, системотехника, исследование операций и сопряженные с ними научные и инженерные направления. [5] Философские категории, используемые в системном анализе Акофф и Эмери пишут: Кибернетики дают цели и информации такие определения, которые как нельзя лучше приспособлены для исследований, проводимых самими кибернетиками. Затем ...
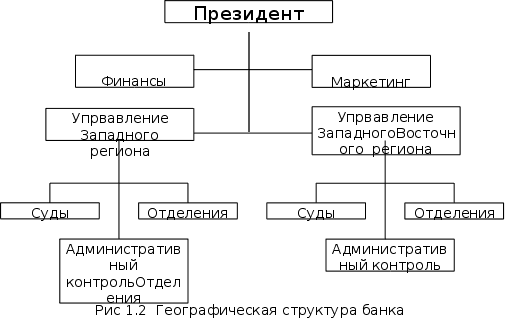
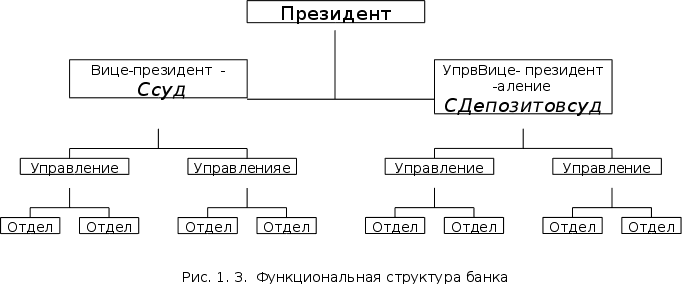
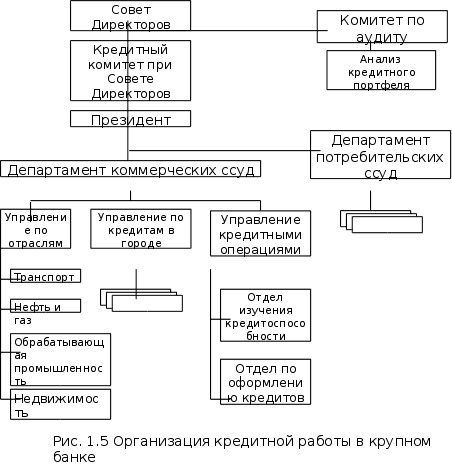
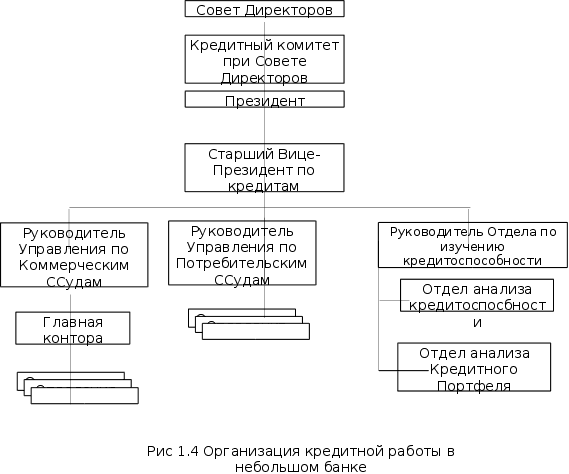
... выявления недостатков и «узких мест» этих систем и подготовке рекомендаций по улучшению функционирования и прогнозированию их развития в условиях информационной неопределенности. Глава 3 Системный анализ управления кредитами.3.1. Анализ кредитных задолженностей в 1995 и 1996 годах. Работа банковской системы любого государства определяется, прежде всего, конечными результатами, представленными в ...
... системы. Главные особенности системного подхода – динамичность, взаимодействие, взаимозависимость и взаимосвязь элементов системы, комплексность, целостность, соподчинённость, выделение ведущего звена. Системный подход в экономическом анализе позволяет разработать научно обоснованные варианты решения хозяйственных задач, определить эффективность этих вариантов, что даёт основание для выбора ...
... , динамические и статические, простые и сложные, естественные и искусственные, с управлением и без управления, непрерывные и дискретные, детерминированные и стохастические, открытые и замкнутые. Основы системного анализа Деление систем на физические и абстрактные позволяет различать реальные системы (объекты, явления, процессы) и системы, являющиеся определенными отображениями (моделями) ре ...


0 комментариев