Навигация
13. Принятие решения.
Предположим, что фирма хочет повысить качество выпускаемой системы. Какие другие системы, кроме анализируемой системы, необходимо при этом учитывать? Объясните, почему на решение этой проблемы влияет то, как устанавливаются границы системы и окружающей среды.
При принятии решения о повышении качества выпускаемой системы - кухонного комбайна, фирме-производителю необходимо учитывать следующие внешние системы:
потребителей, которые предъявляют определённые требования к качеству продукции;
маркетинговую систему, так как сначала необходимо выяснить, какие именно требования предъявляют потребители;
систему своих собственных внутрифирменных ресурсов (человеческих, материальных, финансовых);
производственную систему, то есть производственные возможности и производственные мощности;
систему поставщиков, от которых зависит качество сырья и комплектующих;
технологическую систему, от которой зависит возможность улучшения качественных показателей и технология изготовления;
экономическую систему, от которой зависят финансовые условия деятельности фирмы и выбор стратегии (конкуренция, прибыль, ценообразование, налоги);
систему обеспечения и обслуживания, от которой зависит уровень обслуживания и наличие запасных частей в ремонтных мастерских.
Для того чтобы достичь своей цели фирме-производителю необходимо учитывать очень большое количество факторов. При этом получается так, что все подсистемы объединяются в рамках общей системы, которая устанавливается границы исследуемой системы и окружающей среды. Если что-нибудь изменить внутри этих границ, то в результате снизится возможность достижения именно той цели, которая была поставлена фирмой-производителем или же эта цель вообще станет недостижимой.
Задача № 4Условие задачи.
Дана проблема и возможные варианты её решения (множество допустимых альтернатив) В1, В2, …, Вk (смотри таблицу 1). Каждая альтернатива оценивается множеством (списком) критериев К1, К2, …, Кn (смотри таблицу 1).
Требуется выбрать наилучший вариант решения (наилучшую альтернативу) и оценить последствия выбора (положительные и отрицательные).
При этом для нахождения наилучшего решения используется метод анализа иерархий (метод собственных значений), основанный на аддитивной свёртке.
Таблица 1.
| № варианта задания | Проблема, варианты её решения (множество альтернатив) | Список критериев |
| 3 | Проблема: выбор места работы. Варианты: В1 - частная фирма, В2 - государственное предприятие, В3 - учебный институт. | Оклад, самостоятельность, профессиональный интерес, возможность получения жилплощади, дополнительные нагрузки, дополнительные выгоды, необходимость переобучения, удалённость от дома. |
Решение.
Разбиваем все критерии на 4 группы. После этого составляем общий сквозной список критериев по убыванию важности, причём наиболее важными считаются критерии первой группы, затем второй и третьей.
Функциональные критерии:
оклад
профессиональный интерес
Эргономические критерии:
самостоятельность
возможность получения жилплощади
дополнительные нагрузки
дополнительные выгоды
необходимость переобучения
удалённость от дома
Технико-экономические и специальные критерии - отсутствуют.
Общий сквозной список:
К1 - оклад
К2 - профессиональный интерес
К3 - удалённость от дома
К4 - дополнительные выгоды
К5 - необходимость переобучения
К6 - дополнительные нагрузки
К7 - самостоятельность
К8 - возможность получения жилплощади
Оценим каждую альтернативу (вариант) множеством критериев.
Альтернативы:
В1 - частная фирма.
В2 - государственное предприятие.
В3 - учебный институт.
Оценка:
К1 - В1 > В2 = В3
К2 - В2 > В3 > В1
К3 - В1 = В2 = В3
К4 - В3 > В2 > В1
К5 - В3 > В2 > В1
К6 - В1 > В3 > В2
К7 - В3 > В2 > В1
К8 - В2 > В3 = В1
Проведём попарное сравнение критериев по важности по девятибалльной шкале, и составим соответствующую матрицу (таблица 2) размера (8 x 8):
равная важность - 1,умеренное превосходство - 3,значительное превосходство - 5,сильное превосходство - 7,очень сильное превосходство - 9,в промежуточных случаях ставятся чётные оценки - 2, 4, 6,8.
Таблица 2.
| Критерии | К1 | К2 | К3 | К4 | К5 | К6 | К7 | К8 | НВП |
| К1 | 1 | 1 | 3 | 3 | 5 | 7 | 7 | 9 | 0,293 |
| К2 | 1 | 1 | 2 | 3 | 5 | 7 | 3 | 9 | 0,251 |
| К3 | 1/3 | 1/2 | 1 | 2 | 4 | 7 | 3 | 9 | 0,170 |
| К4 | 1/3 | 1/3 | 1/2 | 1 | 3 | 8 | 3 | 3 | 0,116 |
| К5 | 1/5 | 1/5 | 1/4 | 1/3 | 1 | 5 | 3 | 9 | 0,077 |
| К6 | 1/7 | 1/7 | 1/7 | 1/8 | 1/5 | 1 | 3 | 9 | 0,039 |
| К7 | 1/7 | 1/3 | 1/3 | 1/3 | 1/3 | 1/3 | 1 | 2 | 0,037 |
| К8 | 1/9 | 1/9 | 1/9 | 1/3 | 1/9 | 1/9 | 1/2 | 1 | 0,017 |
| λ max = 8,8480 ИС = 0,1211 ОС = 0,0859 | |||||||||
Нормализованный вектор приоритетов (НВП) определяется по следующей схеме:
а) рассчитывается среднее геометрическое элементов в каждой строке матрицы по формуле:
![]()
б) рассчитывается сумма средних геометрических:
∑= а1 + а2 + … + аn
в) вычисляют компоненты НВП:
аn = аn / ∑.
Каждый компонент НВП представляет собой оценку важности соответствующего критерия.
Проверяется согласованность оценок в матрице. Для этого подсчитываются три характеристики:
а) собственное значение матрицы по формуле:
λ макс = ∑ элементов 1го столбца × 1й компонент НВП + ∑ элементов 2го столбца × 2й компонент НВП + … + ∑ элементов nго столбца × nй компонент НВП,
где × - знак умножения;
![]()
![]() случайной согласованности, определяемый теоретически для случая, когда оценки в матрице представлены случайным образом, и зависящий от размера матрицы. Значения ПСС представлены в таблице 3.
случайной согласованности, определяемый теоретически для случая, когда оценки в матрице представлены случайным образом, и зависящий от размера матрицы. Значения ПСС представлены в таблице 3.
Таблица 3.
| Размер матрицы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| ПСС | 0 | 0 | 0,58 | 0,90 | 1,12 | 1,24 | 1,32 | 1,41 | 1,45 | 1,49 |
Оценки в матрице считаются согласованными, если
ОС ≤ 10 ÷15%.
Проведём попарное сравнение пригодности (ценности) вариантов по каждому критерию по той же шкале, что и для критериев. Для этого необходимо предварительно проранжировать варианты по каждому критерию. Затем полученные результаты занесём в таблицу (таблица 4). В каждом случае подсчитываются:
λimax;
ИСi;
ОСi.
Таблица 4.
| К1 | В1 | В2 | В3 | НВП | К2 | В1 | В2 | В3 | НВП | К3 | В1 | В2 | В3 | НВП |
| В1 | 1 | 5 | 5 | 0,714 | В1 | 1 | 1/5 | 1/3 | 0,105 | В1 | 1 | 1 | 1 | 0,333 |
| В2 | 1/5 | 1 | 1 | 0,143 | В2 | 5 | 1 | 3 | 0,637 | В2 | 1 | 1 | 1 | 0,333 |
| В3 | 1/5 | 1 | 1 | 0,143 | В3 | 3 | 1/3 | 1 | 0,258 | В3 | 1 | 1 | 1 | 0,333 |
| λ 1 max = 3,0000 ИС1 = 0,0000 ОС1 = 0,0000 | λ 2max = 3,0385 ИС2 = 0,0193 ОС2 = 0,0332 | λ 3 max = 3,0000 ИС3 = 0,0000 ОС3 = 0,0000 | ||||||||||||
| К4 | В1 | В2 | В3 | НВП | К5 | В1 | В2 | В3 | НВП | К6 | В1 | В2 | В3 | НВП |
| В1 | 1 | 1/3 | 1/5 | 0,114 | В1 | 1 | 1/3 | 1/5 | 0,114 | В1 | 1 | 5 | 3 | 0,637 |
| В2 | 3 | 1 | 1 | 0,405 | В2 | 3 | 1 | 1 | 0,405 | В2 | 1/5 | 1 | 1/3 | 0,105 |
| В3 | 5 | 1 | 1 | 0,481 | В3 | 5 | 1 | 1 | 0,481 | В3 | 1/3 | 3 | 1 | 0,258 |
| λ 4 max = 3,0291 ИС4 = 0,0145 ОС4 = 0,0251 | λ 5 max = 3,0291 ИС5 = 0,0145 ОС5 = 0,0251 | λ 6 max = 3,0385 ИС6 = 0,0193 ОС6 = 0,0332 | ||||||||||||
| К7 | В1 | В2 | В3 | НВП | К8 | В1 | В2 | В3 | НВП | |||||
| В1 | 1 | 1/3 | 1/5 | 0,114 | В1 | 1 | 1/7 | 1 | 0,111 | |||||
| В2 | 3 | 1 | 1 | 0,405 | В2 | 7 | 1 | 7 | 0,778 | |||||
| В3 | 5 | 1 | 1 | 0,481 | В3 | 1 | 1/7 | 1 | 0,111 | |||||
| λ 7max = 3,0291 ИС7 = 0,0145 ОС7 = 0,0251 | λ 8 max = 3,0000 ИС8 = 0,0000 ОС8 = 0,0000 | |||||||||||||
На этом этапе необходимо подсчитать значение общего критерия для каждого варианта. Для этого значение компонента НВП данного варианта по 1му критерию из таблицы 4 умножается на значение НВП 1го критерия из таблицы 2, затем значение компонента НВП данного варианта по 2му критерию умножается на значение НВП 2го критерия и так далее по всем критериям. Полученные произведения суммируются. В итоге получаем значение общего критерия для 1го варианта решения. Аналогично рассчитывается общий критерий для 2го и 3го вариантов.
К (В1) = 0,714Í0,293 + 0,105Í0,251 + 0,333Í0,170 + 0,114Í0,116 + 0,114Í0,077 + 0,637Í0,039 + 0,114Í0,037 + 0,111Í0,017 = 0,3464
К (В2) = 0,143Í0,293 + 0,637Í0,251 + 0,333Í0,170 + 0,405Í0,116 + 0,405 Í0,077 + 0,105Í0,039 + 0,405Í0,037 + 0,778Í0,017 = 0,3683
К (В3) = 0,143Í0,293 + 0,258Í0,251 + 0,333Í0,170 + 0,481Í0,116 + 0,481Í0,077 + 0,258Í0,039 + 0,481Í0,037 + 0,111Í0,017 = 0,2853
К (В1) = 0,3464 - частная фирма.
К (В2) = 0,3683 - государственное предприятие.
К (В3) = 0,2853 - учебный институт.
Так как метод анализа иерархий (метод собственных значений) основан на аддитивной свёртке, то данный этап решения задачи можно представить ещё и следующим образом по формуле аддитивной свёртки:
![]()
К (х) - общий критерий для альтернативы хЄХ, показывающий её
пригодность для достижения цели,
![]()
аj - относительный вес (важность) частного критерия Kj.
Таблица 5
| аjKj | варианты | ||
| В1 | В2 | В3 | |
| а1К1 | 0,293Í0,714 = 0, 2092 | 0,293Í0,143 = 0,0418 | 0,293Í0,143 = 0,0418 |
| а2К2 | 0,251Í0,105 = 0,0263 | 0,251Í0,637 = 0,1598 | 0,251Í0,258 = 0,0647 |
| а3К3 | 0,170Í0,333 = 0,0566 | 0,170Í0,333 = 0,0566 | 0,170Í0,333 = 0,0566 |
| а4К4 | 0,116Í0,114 = 0,0132 | 0,116Í0,405 = 0,0469 | 0,116Í0,481 = 0,0557 |
| а5К5 | 0,077Í0,114 = 0,0087 | 0,077Í0,405 = 0,0311 | 0,077Í0,481 = 0,0370 |
| а6К6 | 0,039Í0,637 = 0,0248 | 0,039Í0,105 = 0,0040 | 0,039Í0,258 = 0,0100 |
| а7К7 | 0,037Í0,114 = 0,0042 | 0,037Í0,405 = 0,0149 | 0,037Í0,481 = 0,0177 |
| а8К8 | 0,017Í0,111 = 0,0018 | 0,017Í0,778 = 0,0132 | 0,017Í0,111 = 0,0018 |
|
|
|
| |
Для весов выполняется условие нормировки ![]() , которое необходимо, чтобы результаты, полученные в разных условиях, были сопоставимы.
, которое необходимо, чтобы результаты, полученные в разных условиях, были сопоставимы.
В нашем случае:
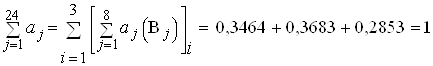 ,
,
то есть условие нормировки выполняется.
Наилучшее решение определяем по выражению:
![]()
К (х) - одна из свёрток выбираемых ЛПР, в нашем случае аддитивная свёртка.
Итак, по расчётам видно, что наибольшее значение критерия имеет второй вариант (В2) (0,3683), который является предпочтительным перед остальными.
На этом этапе проверяется достоверность решения, для чего подсчитываются:
обобщённый индекс согласования (ОИС),
обобщённый показатель случайной согласованности (ОПСС),
обобщённое отношение согласованности (ООС).
1. ОИС подсчитывается по следующей формуле:
ОИС = ИС1 Í НВП (К1) + ИС2 Í НВП (К2) + … + ИС8 Í НВП (К8)
При этом:
ИСi берётся из таблицы 4.
НВП (Кj) берётся из таблицы 2.
ОИС = 0,000 Í 0,293 + 0,0193 Í 0,251 + 0,000 Í 0,170 + 0,0145 Í 0,116 + 0,0145Í0,077 + 0,0193 Í 0,039 + 0,0145 Í 0,037 + 0,000 Í 0,017 = 0,0089
2. ОПСС подсчитывается так же как и ОИС, с той разницей, что вместо ИС1, ИС2 и так далее из таблицы 4 подставляются ПСС, соответствующие размеру матриц сравнения вариантов из таблицы 3. В данном случае размер матрицы 3, поэтому ПСС = 0,58.
ОПСС = 0,58 Í 0,293 + 0,58 Í 0,251 + 0,58 Í 0,170 + 0,58 Í 0,116 + 0,58 Í 0,077 + 0,58 Í 0,039 + 0,58 Í 0,037 + 0,58 Í 0,017 = 0,58
3. ООС рассчитывается по следующей формуле:
![]()
Решение считается достоверным, если ООС ≤ 10 ÷ 15%.
![]()
ООС удовлетворяет условию, а значит, решение является достоверным.
В заключении оценим положительные и отрицательные последствия данного решения.
Напомним, что по условию задачи была поставлена проблема:
выбор места работы.
Также были предложены три варианта решения данной проблемы:
В1 - частная фирма,
В2 - государственное предприятие,
В3 - учебный институт.
В процессе решения задачи было выявлено, что наиболее предпочтительным является второй вариант, а именно государственное предприятие.
Положительные последствия данного решения:
социальная защищённость;
экономическая стабильность и защищённость;
нормированный рабочий день;
гарантированный отпуск;
возможность получения вознаграждений за дополнительные нагрузки;
возможность профессионального роста;
возможность получения различного вида льгот;
определённая уверенность в будущем.
Отрицательные последствия данного решения:
низкий уровень заработной платы (в частных фирмах, как правило, заработная плата выше);
ежемесячные авралы в конце каждого месяца и как следствие дополнительные нагрузки;
возможность увеличения различного вида нагрузок за ту же зарплату;
возможность материального наказания за произведённый брак (плохо выполненную услугу или работу);
зачастую косность мышления руководства и как следствие отсутствие возможности реализации своих собственных идей.
Следует иметь в виду, что для принятия обоснованного решения обычно приходится использовать несколько методов. Поэтому результат, полученный методом анализа иерархий, проверяется другими методами в задаче № 5.
Задача № 5
Условие задачи.
По данным предыдущей задачи найдите наилучшее решение, используя следующие методы:
свёртку по наихудшему критерию (с учётом важности критериев);
свёртку по наихудшему критерию (без учёта важности критериев);
метод главного критерия;
мультипликативную свёртку;
свёртку по наилучшему критерию;
аддитивную свёртку (с использованием функции полезности);
метод расстояния.
Обоснуйте применимость каждого метода, объясните полученные результаты и сделайте выводы.
Решение.
Свёртка по наихудшему критерию с учётом важности критериев.
Данная свёртка соответствует стратегии “пессимизма", при которой решение принимается по критерию, имеющему наименьшее значение. По таблице 5 из задачи 4 находим данные, используя формулу:
![]()
В1: К (х) = min а8 K8 = 0,0018
В2: К (х) = min а6 K6 = 0,0040
В3: К (х) = min а8 K8 = 0,0018
Наилучшее решение определяем по выражению:
![]()
Наибольшее значение критерия имеет второй вариант (В2), который является предпочтительным перед остальными.
Свёртка по наихудшему критерию без учёта важности критериев.
На основе данных таблицы 5 из задачи 4, и используя формулу:
![]() , где аj = const (j) = 1/n = 1/8
, где аj = const (j) = 1/n = 1/8
производим расчёт:
В1: К (х) = min 1/8K2 = 0,125 x 0,105 = 0,0131
В2: К (х) = min 1/8K6 = 0,125 x 0,105 = 0,0131
В3: К (х) = min 1/8K8 = 0,125 x 0,111 = 0,0138
Наилучшее решение определяем по выражению:
![]()
Наибольшее значение критерия имеет третий вариант (В3), который является предпочтительным перед остальными.
Метод главного критерия.
Данный метод, можно применять в тех случаях, когда один из критериев значительно превосходит все остальные критерии (в три и более раз), если же это условие не выполняется, то данный метод применять не рекомендуется. Тот вариант, для которого значение главного критерия максимально, является наилучшим.
В данном случае главным критерием является критерий К1, хотя считать его главным можно лишь с оговоркой, так как он не превышает все остальные критерии в 3 и более раз. На основе данных таблицы 5 получаем:
К (В1) = 0, 2092
К (В2) = 0,0418
К (В3) = 0,0418
Наибольшее значение критерия имеет первый вариант (В1).
Мультипликативная свёртка.
Данная свёртка позволяет учесть критерии, имеющие малые (по модулю) значения, то есть наибольший вклад дают множители наименьшие по модулю. На основе данных таблицы 4 из задачи 4, производим расчёт:
![]()
К (В1) = 0,7140,293 Í 0,1050,251 Í 0,3330,170 Í 0,1140,116 Í 0,1140,077 Í 0,6370,039 Í
0,1140,037 Í 0,1110,017 = 0,9060 Í 0,5679 Í 0,8294 Í 0,7773 Í 0,8460 Í
0,9825 Í 0,9227 Í 0,9633 = 0,2450
К (В2) = 0,1430,293 Í 0,6370,251 Í 0,3330,170 Í 0,4050,116 Í 0,4050,077 Í 0,1050,039 Í
0,4050,037 Í 0,7780,017 = 0,5656 Í 0,8929 Í 0,8294 Í 0,9004 Í 0,9327 Í
0,9158 Í 0,9671 Í 0,9957 = 0,3102
К (В3) = 0,1430,293 Í 0,2580,251 Í 0,3330,170 Í 0,4810,116 Í 0,4810,077 Í 0,2580,039 Í
0,4810,037 Í 0,1110,017 = 0,5656 Í 0,7117 Í 0,8294 Í 0,9186 Í 0,9452 Í
0,9485 Í 0,9732 Í 0,9633 = 0,2577
К (В1) = 0,2450
К (В2) = 0,3102
К (В3) = 0,2577
Наибольшее значение критерия имеет второй вариант (В2), который является предпочтительным перед остальными.
Свёртка по наилучшему критерию.
Данный метод соответствует стратегии “оптимизма". На основе данных таблицы 5 из задачи 4 выбираем наибольшее значение произведений аjKj (Bj) для каждого варианта. Вариант, которому оно соответствует, - наилучший.
а1 K1 (B1) = 0, 2092
Наибольшее значение критерия имеет первый вариант (В1), который является предпочтительным перед остальными.
Аддитивная свёртка (с использованием функции полезности).
Данный метод позволяет учесть критерии, имеющие большие (по модулю) значения.
Используя данные таблицы 4 из задачи 4, оценим по 10-и балльной шкале полезность (ценность) каждого варианта по каждому критерию. Наименьшее значение принимаем за 1.
По критерию К1:
В1 = 8/ (8 + 1 + 1) Í 10 = 8/10 Í 10 = 0,8 Í 10 = 8
В2 = 1/ (8 + 1 + 1) Í 10 = 1/10 Í 10 = 0,1 Í 10 = 1
В3 = 1/ (8 + 1 + 1) Í 10 = 1/10 Í 10 = 0,1 Í 10 = 1
По критерию К2:
В1 = 1/ (1 + 6 + 3) Í 10 = 1/10 Í 10 = 0,1 Í 10 = 1
В2 = 6/ (1 + 6 + 3) Í 10 = 6/10 Í 10 = 0,6 Í 10 = 6
В3 = 3/ (1 + 6 + 3) Í 10 = 3/10 Í 10 = 0,3 Í 10 = 3
И так далее по всем критериям. Полученные результаты занесём в таблицу 1.
Таблица 1
| К1 | К2 | К3 | К4 | К5 | К6 | К7 | К8 | |
| В1 | 8 | 1 | 3 | 1 | 1 | 6 | 1 | 1 |
| В2 | 1 | 6 | 3 | 4 | 4 | 1 | 4 | 8 |
| В3 | 1 | 3 | 3 | 5 | 5 | 3 | 5 | 1 |
Теперь, используя данные полученной таблицы и оценки важности критериев по таблице 2 из задачи 4, найдём наилучшее решение.
К (В1) = 0,293×8 + 0,251×1 + 0,170×3 + 0,116×1 + 0,077×1 + 0,039×6 + 0,037×1 + 0,017×1 = 2,344 + 0,251 + 0,510 + 0,116 + 0,077 + 0,234 + 0,037 + 0,017 = 3,586
К (В2) = 0,293×1 + 0,251×6 + 0,170×3 + 0,116×4 + 0,077×4 + 0,039×1 + 0,037×4 + 0,017×8 = 0,293 + 1,506 + 0,510 + 0,464 + 0,308 + 0,039 + 0,148 + 0,136 = 3,404
К (В3) = 0,293×1 + 0,251×3 + 0,170×3 + 0,116×5 + 0,077×5 + 0,039×3 + 0,037×5 + 0,017×1 = 0,293 + 0,753 + 0,510 + 0,580 + 0,385 + 0,117 + 0,185 + 0,017 = 2,840
К (В1) = 3,586
К (В2) = 3,404
К (В3) = 2,840
Наибольшее значение критерия имеет первый вариант (В1), который является предпочтительным перед остальными.
Метод расстояния (введения метрики).
Данный метод можно применять в тех случаях, когда по условиям задачи можно определить идеальное решение (Вид), имеющий абсолютный максимум сразу по всем критериям.
Идеальное решение определяем, используя данные таблицы 4 из задачи 4. В качестве координат абсолютного максимума выбираем наибольшее значение НВП по каждому критерию, а именно:
К1 (Вид) = 0,714
К2 (Вид) = 0,637
К3 (Вид) = 0,333
К4 (Вид) = 0,481
К5 (Вид) = 0,481
К6 (Вид) = 0,637
К7 (Вид) = 0,481
К8 (Вид) = 0,778
На основе выявленных данных подсчитаем значение меры расстояния для каждого варианта решения, используя функцию Минковского:
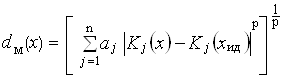 , где
, где
p - постоянная Минковского.
Похожие работы
... , телеология, теория информации, инженерная теория связи, теория ЭВМ, системотехника, исследование операций и сопряженные с ними научные и инженерные направления. [5] Философские категории, используемые в системном анализе Акофф и Эмери пишут: Кибернетики дают цели и информации такие определения, которые как нельзя лучше приспособлены для исследований, проводимых самими кибернетиками. Затем ...
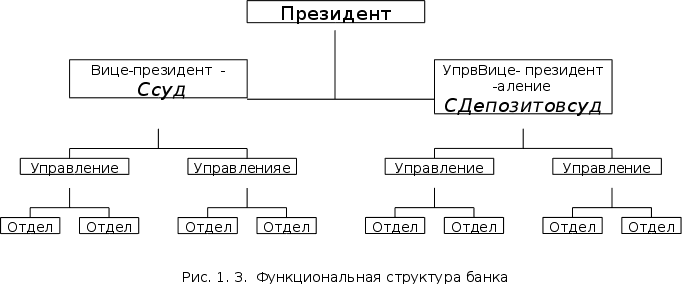
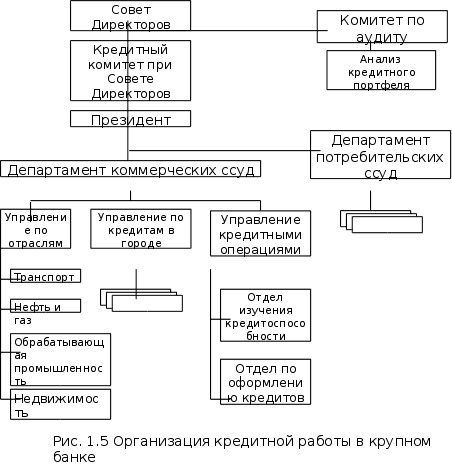
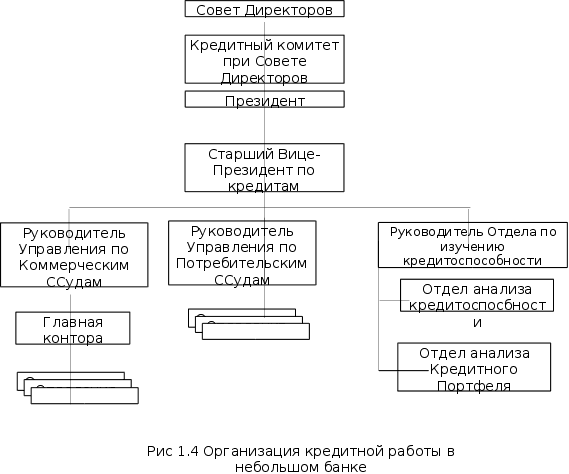
... выявления недостатков и «узких мест» этих систем и подготовке рекомендаций по улучшению функционирования и прогнозированию их развития в условиях информационной неопределенности. Глава 3 Системный анализ управления кредитами.3.1. Анализ кредитных задолженностей в 1995 и 1996 годах. Работа банковской системы любого государства определяется, прежде всего, конечными результатами, представленными в ...
... системы. Главные особенности системного подхода – динамичность, взаимодействие, взаимозависимость и взаимосвязь элементов системы, комплексность, целостность, соподчинённость, выделение ведущего звена. Системный подход в экономическом анализе позволяет разработать научно обоснованные варианты решения хозяйственных задач, определить эффективность этих вариантов, что даёт основание для выбора ...
... , динамические и статические, простые и сложные, естественные и искусственные, с управлением и без управления, непрерывные и дискретные, детерминированные и стохастические, открытые и замкнутые. Основы системного анализа Деление систем на физические и абстрактные позволяет различать реальные системы (объекты, явления, процессы) и системы, являющиеся определенными отображениями (моделями) ре ...


0 комментариев