Обобщение как усиление. Этот метод поясняем на примере доказательства неравенства

6.  Обобщение как усиление. Этот метод поясняем на примере доказательства неравенства

.

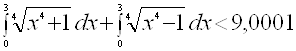Введем функцию . Легко убедиться, что при  она возрастает и график является выпуклым вниз (рис. 1).

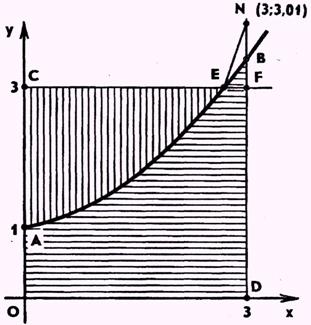
рис. 1

Рассмотрим криволинейную трапецию . Очевидно, что ее площадь  может быть вычислена по формуле

.

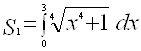Площадь криволинейного треугольника  находится по формуле

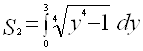, или .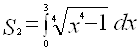

Отсюда ясно, что в условии предлагается доказать, что

.

Так как площадь квадрата  равна , то достаточно убедиться, что площадь криволинейного треугольника  меньше . Укажем координаты “нужных” точек:

.

Теперь рассмотрим точку . Пользуясь выпуклостью вниз графика функции , легко убедиться, что площадь криволинейного треугольника  меньше площади треугольника . Докажем неравенство  (это больше, чем нам нужно):

.

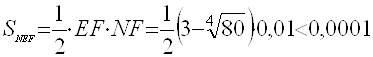Отсюда и получаем требуемое неравенство.

7.  Обобщение на основе соединения. При данном способе обобщения новые утверждения получаются путем рассмотрения свойств объектов из разных тем (отметим, что этот метод отражен в названии наук – биофизика, биохимия, математическая биология и др.).

Известны следующие утверждения:

1. а) Если  и  - корни трехчлена , то .

б) Если  и  - любые числа, а , , то  и  - корни уравнения .

2. Пусть  - точка касания вписанной в прямоугольный треугольник окружности с гипотенузой  и ,  (рис. 2). Доказать, что площадь треугольника равна .

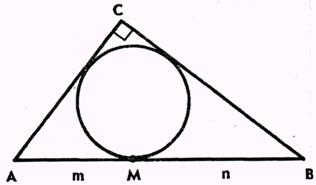
рис. 2

Соединяя эти утверждения, можем сформулировать следующие задания:

Если  и  - отрезки, на которые точка касания окружности, вписанной в прямоугольный треугольник, разбивает гипотенузу, то:

 

а) ;

б) ;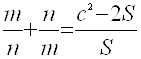

в) ,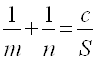

 

где  - гипотенуза, а  - площадь треугольника.

ОБОБЩЕНИЯ ПРИ РЕШЕНИИ ЗАДАЧ НА УРОКАХ МАТЕМАТИКИ

 

Обобщение в преподавании математики

 

При обобщении мысленно выявляют какое-нибудь свойство, принадлежащее множеству объектов и объединяющее эти объекты воедино.

Так, например, изучение формулы n-го члена арифметической прогрессии начинается с рассмотрения конкретных примеров на вычисление различных членов арифметической прогрессии по заданным первому ее члену и разности.

При проведении этих вычислений учащиеся используют равенства:

 

a₂ = a₁ + d,

a₃ = a₂ + d = (a₁ + d) + d = a₁ + 2d,

a₄ = a₃ + d = (a₁ + 2d) + d = a₁ + 3d и т. д.

Естественно, возникает полезное обобщение эти равенств в одной формуле a_n = a₁ + d(n – 1), с помощью которой устанавливается более короткий способ для вычисления любого члена арифметической прогрессии.

В дальнейшем эта формула получает новое обобщение, когда устанавливается, что любая арифметическая прогрессия является линейной функцией натурального аргумента:

 

y = kx + b, где xN.

Можно сказать, что обобщение выступает как переход от данного множества предметов к рассмотрению более «емкого» множества, содержащего данное.

Так, например, мы обобщаем, когда переходим от рассмотрения множества натуральных чисел к множеству дробных положительных чисел.

К обобщению могут привести: а) замена некоторой постоянной объекта переменной (треугольник многоугольник); б) отказ от ограничения, наложенного на объект изучения D (D – множество действительных чисел).

Обобщение есть переход от рассмотрения единственного объекта к рассмотрению некоторого множества, содержащего этот объект в качестве своего элемента, или переход от менее емкого множества к более емкому, содержащему первоначальное.