2. Предел функции
При исследовании графиков различных функций можно видеть, что при неограниченном стремлении аргумента функции к какой-то величине, то ли конечной, то ли бесконечной, сама функция также может принимать ряд значений, неограниченно приближающихся к некоторой величине. Следовательно, для функции также можно ввести понятие предела.
Определение 2.1. Число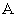 
называется пределом функции 
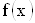в точке 
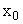, если для любого 
существует такое число 
, что из условия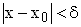 
следует, что 
.
Данное условие записывается в виде: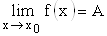 
. Отметим, что интервал длины 
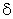, который содержит в себе точку 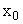, называется 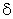-окрестностью точки .
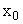Аналогичным образом вводится понятие предела функции и при стремлении 
к 
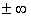. Так же как и в случае числовой последовательности, для функции существует теорема Коши, которая определяет существование у нее предела.
Теорема Коши о существовании предела. Для того чтобы функция 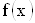, где 
, имела предел 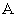при 
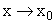, где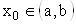 
, необходимо и достаточно, чтобы для любого существовало такое число , что из условия 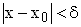вытекало условие .
Доказательства теоремы приводить не будем. В качестве предела функции могут служить как конечные, так и бесконечные величины.
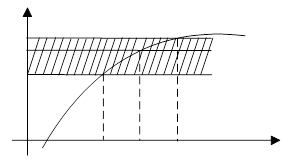
Геометрический смысл теоремы Коши заключается в следующем. Возьмем некоторое 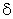, для которого 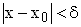. Тогда, согласно теореме, . Представим данное неравенство следующим образом: 
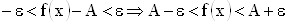. Иначе говоря, как только станет отличаться от 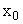меньше, чем на 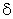, сама функция окажется в полосе шириной 
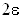, расположенной на линии 
.
В приведенном определении предела и теореме Коши может стремиться к 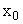произвольным образом. Однако во многих случаях это стремление происходит с какой-то одной стороны. Для этого вводятся понятия односторонних пределов.
Определение 2.2. Если стремится к 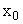, оставаясь все время меньше его, и при этом 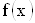стремится к 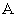, то это число называется пределом функции слева и обозначается 
.
Определение 2.3. Если стремится к 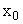, оставаясь все время больше его, и при этом 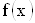стремится к 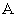, то это число называется пределом функции справа и обозначается 
.
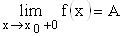Необходимо иметь в виду, что не всегда пределы слева и справа в точке 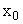равны между собой.
Раздел:
Математика Количество знаков с пробелами: 10638
Количество таблиц: 1
Количество изображений: 1
... Зенона и решение их Аристотелем Исторический анализ позволяет по-новому увидеть и глубже понять смысл современных дискуссий, посвященных проблеме континуума и различных его видов. В своей работе мы коснемся лишь наиболее важных, узловых моментов в истории понятия непрерывности, начиная с античности и кончая XVII–ХVIII вв. Как уже упоминалось, впервые проблема континуума была поставлена Зеноном ...
... ,
ведении войны,
обороне и т.д.
Таким образом,
культура - это
класс символизированных предметов и
явлений, рассматриваемых
в экстрасоматическом
контексте.
До
появления
культурологии
в процессе
расширения
сферы наукиi
натуралистическое
(т.е. немифологическое,
нетеологическое)
объяснение
поведения людей
носило биологический,
психологический
или социологический характер.
Соответственно
то или иное
...
... и докажите сходимость полученного разложения к порождающей функции. Исследовать на абсолютную и условную сходимость .
Зав. кафедрой
--------------------------------------------------
Экзаменационный
билет по предмету
МАТЕМАТИЧЕСКИЙ
АНАЛИЗ
Билет № 12 Сформулируйте теорему Ролля и объясните ее геометрический смысл. Исследуйте функцию на выпуклость и вогнутость. Какая ...
... наибольших, наименьших значений функций. 4. Нахождения дифференциала для приближенных вычислений. 5. Для доказательства неравенств. Рассмотрю некоторые примеры применения производной в алгебре, геометрии и физике. Задача 1. Найти сумму 1+2*1/3+3(1/3)2+…+100(1/3)99; Решение. Найду сумму g(x)=1+2x+3x2+…+100x99 и подставлю в нее x=1/3. Для этого потребуется ...
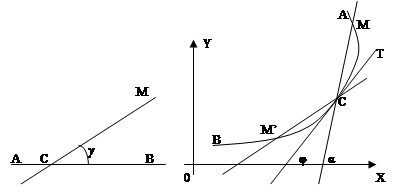
0 комментариев