Навигация
4. Формула Пуассона
Эта формула применяется при неограниченном возрастании числа испытаний, когда вероятность наступления события достаточно близка к 0 или 1.
![]() ,
,
где ![]() .
.
Доказательство.
![]()
![]() .
.
![]() .
.
Таким образом получили формулу:
![]() .
.
Примеры
№17. Вероятность изготовления негодной детали равна 0,0002. Найти вероятность того, что среди 10000 деталей только 2 детали будут негодными.
Решение. n=10000; k=2; p=0,0002. ![]()
Искомая вероятность
![]() .
.
№18. Вероятность изготовления бракованной детали равна 0,0004. Найти вероятность того, что среди 1000 деталей только 5 детали будут бракованными.
Решение. n=1000; k=5; p=0,0004.
![]()
Искомая вероятность
![]() .
.
№19. Вероятность выигрыша лотереи равна 0,0001. Найти вероятность того, что из 5000 попыток выиграть удастся 3 раза.
Решение. n=5000; k=3; p=0,0001.
![]()
Искомая вероятность
![]() .
.
5. Теорема Бернулли о частоте вероятности
Теорема. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p, абсолютная величина отклонения относительной частоты появления события от вероятности появления события не превысит положительного числа ![]() , приближенно равна удвоенной функции Лапласа при
, приближенно равна удвоенной функции Лапласа при ![]() :
:
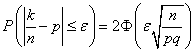 .
.
Доказательство. Будем считать, что производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна p. Поставим перед собой задачу найти вероятность того, что отклонение относительной частоты ![]() от постоянной вероятности p по абсолютной величине не превышает заданного числа
от постоянной вероятности p по абсолютной величине не превышает заданного числа ![]() . Другими словами, найдем вероятность осуществления неравенства
. Другими словами, найдем вероятность осуществления неравенства
![]() . (*)
. (*)
Заменим неравенство (*) ему равносильными:
![]() .
.
Умножая эти неравенства на положительный множитель ![]() , получим неравенства, равносильные исходному:
, получим неравенства, равносильные исходному:
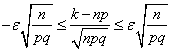 .
.
Тогда вероятность найдем следующим образом:
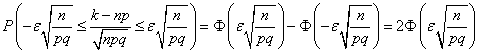 .
.
Значение функции ![]() находится по таблице(см. приложение2).
находится по таблице(см. приложение2).
Примеры
№20. Вероятность того, что деталь не стандартна, p=0,1. Найти вероятность того, что среди случайно отобранных 400 деталей относительная частота появления нестандартных деталей отклонится от вероятности p=0,1 по абсолютной величине не более, чем на 0,03.
Решение. n=400; p=0,1; q=0,9; ![]() =0,03. Требуется найти вероятность
=0,03. Требуется найти вероятность![]() . Пользуясь формулой
. Пользуясь формулой
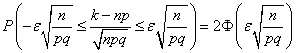 ,
,
имеем
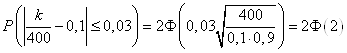 .
.
По таблице приложения2 находим ![]() . Следовательно,
. Следовательно, ![]() . Итак, искомая вероятность равна 0,9544.
. Итак, искомая вероятность равна 0,9544.
№21. Вероятность того, что деталь не стандартна, p=0,1. Найти, сколько деталей надо отобрать, чтобы с вероятностью, равной 0,9544, можно было утверждать, что относительная частота появления нестандартных деталей(среди отобранных) отклонится от постоянной вероятности p по абсолютной величине не более чем на 0,03.
Решение. По условию, p=0,1; q=0,9; ![]() =0,03;
=0,03; ![]() . Требуется найти n. Воспользуемся формулой
. Требуется найти n. Воспользуемся формулой
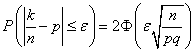 .
.
В силу условия
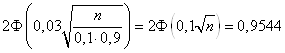
Следовательно,
![]()
По таблице приложения 2 находим ![]() . Для отыскания числа n получаем уравнение
. Для отыскания числа n получаем уравнение ![]() . Отсюда искомое число деталей n=400.
. Отсюда искомое число деталей n=400.
№22. Вероятность появления события в каждом из независимых испытаний равна 0,2. Найти, какое отклонение относительной частоты появления события от его вероятности можно ожидать с вероятностью 0,9128 при 5000 испытаниях.
Решение. Воспользуемся той же формулой, из которой следует:
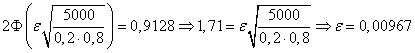 .
.
Литература
1. Гмурман Е.В. "Теория вероятностей и математическая статистика", Москва, "Высшая школа"2003.
2. Гмурман Е.В. "Руководство к решению задач по теории вероятностей и математической статистике", Москва "Высшая школа"2004.
3. Гнеденко Б.В. "Курс теории вероятностей", Москва, "Наука"1988.
4. Колемаев В.А., Калинина В.Н., Соловьев В.И., Малыхин В.И., Курочкин А.П. "Теория вероятностей в примерах и задачах", Москва, 2001.
5. Вентцель Е.С. "Теория вероятностей", Москва, "Высшая школа"1998.
Приложения
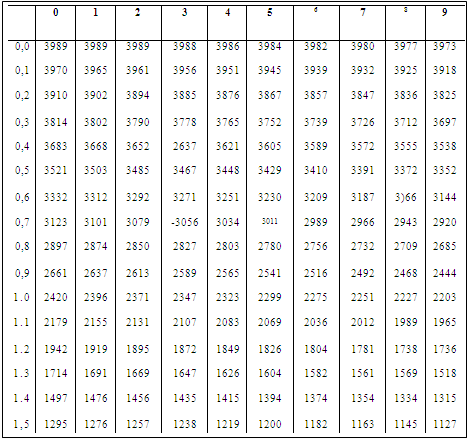
Приложение 1
Таблица значений функции ![]()
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1.6 | 1109 | 1092 | 1074 | 1057 | 1040 | 1023 | 1006 | 0989 | 0973 | 0957 |
| 1.7 | 0940 | 0925 | 0909 | 0893 | 0878 | 0863 | 0648 | 0833 | 0818 | 0804 |
| 1.8 | 0790 | 0775 | 0761 | 0748 | 0734 | 0721 | 0707 | 0694 | 0681 | 0669 |
| 1.9 | 0656 | 0644 | 0632 | 0620 | 0608 | 0596 | 0584 | 0573 | 0562 | 0551 |
| 2,0 | 0540 | 0529 | 0519 | 0508 | 0498 | 0488 | 0478 | 0468 | 0459 | 0449 |
| 2.1 | 0440 | 0431 | 0422 | 0413 | 0404 | 0396 | 0387 | 0379 | 0371 | 0363 |
| 2.2 | 0355 | 0347 | 0339 | 0332 | 0325 | 0317 | 0310 | 0303 | 0297 | 0290 |
| 2.3 | 0283 | 0277 | 0270 | 0264 | 0258 | 0252 | 0246 | 0241 | 0235 | 0229 |
| 2,4 | 0224 | 0219 | 0213 | 0208 | 0203 | 0198 | 0194 | 0189 | 0184 | 0180 |
| 2.5 | 0175 | 0171 | 0167 | 0163 | 0158 | 0154 | 0151 | 0147 | 0143 | 0139 |
| 2.6 | 0136 | 0132 | 0129 | 0126 | 0122 | 0119 | 0116 | 0113 | 0110 | 0107 |
| 2,7 | 0104 | 0101 | 0099 | 0096 | 0093 | 0091 | 0088 | 0086 | 0084 | 0081 |
| 2,8 | 0079 | 0077 | 0075 | 0073 | 0071 | 0069 | 0067 | 0065 | 0063 | 0061 |
| 2.9 | 0060 | 0058 | 0056 | 0055 | 0053 | 0051 | 0050 | 0048 | 0047 | 0043 |
| 3,0 | 0044 | 0043 | 0042 | 0040 | 0039 | 0038 | 0037 | 0036 | 0035 | 0034 |
| 3,1 | 0033 | 0032 | 0031 | 0030 | 0029 | 0028. | 0027 | 0026 | 0025 | 0025 |
| 3,2 | 0024 | 0023 | 0622 | 0022 | 0021 | 0020 | 0020 | 0019 | 0018 | 0018 |
| 3,3 | 0017 | 0017 | 0016 | 0016 | 0015 | 0015 | 0014 | 0014 | 0013 | 0013 |
| 3,4 | 0012 | 0012 | 0012 | 0011 | 0011 | 0010 | 0010 | 0010 | 0009 | 0009 |
| 3,5 | 0009 | 0008 | 0008 | 0008 | 0008 | 0007 | 0007 | 0007 | 0007 | 0006 |
| 3,6 | 0006 | 0006 | 0006 | 0005 | 0005 | 0005 | 0005 | 0005 | 0005 | 0004 |
| 3,7 | 0004 | 0004 | 0004 | 0004 | 0004 | 0004 | 0003 | 0003 | 0003 | 0003 |
| 3,8 | 0003 | 0003 | 0003 | 0003 | 0003 | 0002 | 0002 | 0002 | 0002 | 0002 |
| 3,9 | 0002 | 0002 | 0002 | 0002 | 0002 | 0002 | 0002 | 0002 | 0001 | 0001 |
Приложение 2
Таблица значений функции ![]()
| x |
| x |
| x |
| x |
|
| 0900 | 0,0000 | 0,32 | 0,1255 | 0,64 | 0,2389 | 0,96 | 0,3315 |
| 0,01 | 0,0040 | 0,33 | 0,1293 | 0,65 | 0,2422 | 0,97 | 0,3340 |
| 0,02 | 0,0080 | 0,34 | 0,1331 | 0,66 | 0,2454 | 0,98 | 0,3365 |
| 0,03 | 0,0120 | 0,35 | 0,1368 | 0,67 | 0,2486 | 0.99 | 0,3389 |
| 0,04 | 0,0160 | 0,36 | 0,1406 | 0,68 | 0,2517 | 1,00 | 0,3413 |
| 0,05 | 0,0199 | 0,37 | 0,1443 | 0,69 | 0,2549 | 1,01 | 0,3438 |
| 0,06 | 0,0239 | 0,38 | 0,1480 | 0,70 | 0,2580 | 1,02 | 0,3461 |
| 0,07 | 0,0279 | 0,39 | 0,1517 | 0,71 | 0,2611 | 1,03 | 0,3485 |
| 0,08 | 0,0319 | 0,40 | 0,1554 | 0,72 | 0,2642 | 1,04 | 0,3508 |
| 0,09 | 0,0359 | 0,41 | 0,1591 | 0,73 | 0,2673 | 1,05 | 0,3531 |
| 0,10 | 0,0398 | 0,42 | 0,1628 | 0,74 | 0,2703 | 1,06 | 0,3554 |
| 0,11 | 0,0438 | 0,43 | 0,1664 | 0,75 | 0,2734 | 1,07 | 0,3577 |
| 0,12 | 0,0478 | 0,44 | 0,1700 | 0,76 | 0,2764 | 1,08 | 0,3599 |
| 0,13 | 0,0517 | 0,45 | 0,1736 | 0,77 | 0,2794 | 1.09 | 0,3621 |
| 0,14 | 0,0557 | 0,46 | 0,1772 | 0,78 | 0,2823 | 1.10 | 0,3643 |
| 0,15 | 0,0596 | 0,47 | 0,1808 | 0,79 | 0,2852 | 3665 | 0,3665 |
| 0,16 | 0,0636 | 0,48 | 0,1844 | 0,80 | 0,2881 | 3686 | 0,3686 |
| 0,17 | 0,0675 | 0,49 | 01879 | 0,81 | 0,2910 | 1,13 | 0,3708. |
| 0,18 | 0,0714 | 0,50 | 0,1915 | 0,82 | 0,2939 | 1,14 | 0,3729 |
| 0,19 | 0,0753 | 0,51 | 0,1950 | 0,83 | 0,2967 | 1,15 | 0,3749 |
| 0,20 | 0,0793 | 0,52 | 0,1985 | 0,84 | 0,2995 | 1,16 | 0,3770 |
| 0,21 | 0,0832 | 0,53 | 0,2019 | 0,85 | 0,3023 | 1,17 | 0,3790 |
| 0,22 | 0,0871 | 0,54 | 0,2054 | 0,86 | 0,3051 | 1,18 | 0,3810 |
| 0,23 | 0,0910 | 0,55 | 0,2088 | 0,87 | 0,3078 | 1,19 | 0,3830 |
| 0,24 | 0,0948 | 0,56 | 0,2123 | 0,88 | 0,3106 | 1,20 | 0,3849 |
| 0,25 | 0,0987 | 0,57 | 0,2157 | 0,89 | 0,3133 | 1.21 | 0,3869 |
| 0,26 | 0,1026 | 0,58 | 0,2190 | 0,90 | 0,3159 | 1,22 | 0/3883 |
| 0,27 | 0,1064 | 0,59 | 0,2224 | 0,91 | 0,3186 | 1,23 | 0,3907 |
| 0,28 | 0,1103 | 0,60 | 0,2257 | 0,92 | 0,3212 | 1.24 | 0,3925 |
| 0,29 | 0,1141 | 0,61 | 0,2291 | 0,93 | 0,3238 | 1,25 | 0,3944 |
| 0,30 | 0,1179 | 0,62 | 0,2324 | 0,94 | 0,3264 | ||
| 0,31 | 0,1217 | 0,63 | 0,2357 | 0,95 | 0,3289 |
| x |
| x | | x |
| x |
|
| 1,26 | 0,3962 | 1,59 | 0,4441 | 1,92 | 0,4726 | 2,50 | 0,4938 |
| 1,27 | 0,3980 | 1,60 | 0,4452 | 1,93 | 0,4732 | 2,52 | 0,4941 |
| 1,28 | 0,3997 | 1,61 | 0,4463 | 1,94 | 0,4738 | 2,54 | 0,4945 |
| 1,29 | 0.4015 | 1,62 | 0,4474 | 1,95 | 0,4744 | 2,56 | 0,4948 |
| 1,30 | 0,4032 | 1,63 | 0.4484 | 1.96 | 0,4750 | 2,58 | 0,4951 |
| 1,31 | 0,4049 | 1,64 | 0,4495 | 1,97 | 0,4756 | 2,60 | 0,4953 |
| 1,32 | 0.4066 | 1,65 | 0,4505 | 1,98 | 0,4761 | 2,62 | 0,4956 |
| 1,33 | 0,4082 | 1,66 | 0,4515 | 1,99 | 0,4767 | 2,64 | 0,4959 |
| 1,34 | 0.4099 | 1,67 | 0.4525 | 2.00 | 0,4772 | 2,66 | 0,4961 |
| 1.3S | 0.4115 | 1,68 | 0,4535 | 2,02 | 0,4783 | 2,68 | 0,4963 |
| 1,36 | 0.4131 | 1,69 | 0,4545 | 2,04 | 0,4793 | 2,70 | 0,4965 |
| 1,37 | 0.4147 | 1,70 | 0,4554 | 2,06 | 0,4803 | 2,72 | 0,4967 |
| 1,38 | 0.4162 | 1.71 | 0,4564 | 2,08 | 0,4812 | 2,74 | 0,4969 |
| 1,39 | 0.4177 | 1,72 | 0,4573 | 2,10 | 0,4821 | 2,76 | 0,4971 |
| 1.40 | 0,4192 | 1,73 | 0,4582 | 2,12 | 0,4830 | 2,78 | 0,4973 |
| 1.41 | 0,4207 | 1.74 | 0,4591 | 2,14 | 0,4838 | 2,80 | 0,4974 |
| 1.42 | 0.4222 | 1,75 | 0.4599 | 2,16 | 0,4846 | 2,82 | 0,4976 |
| 1.43 | 0.4236 | 1,76 | 0,4608 | 2,18 | 0,4854 | 2,84 | 0,4977 |
| 1.44 | 0,4251 | 1.77 | 0,4616 | 2,20 | 0,4861 | 2,86 | 0,4979 |
| 1,45 | 0.4265 | 1,78 | 0.4625 | 2,22 | 0,4868 | 2,88 | 0,4980 |
| 1.46 | 0,4279 | 1,79 | 0,4633 | 2,24 | 0,4875 | 2,90 | 0,4981 |
| 1.47 | 0,4292 | 1,80 | 0,4641 | 2,26 | 0,4881 | 2,92 | 0,4982 |
| 1,48 | 0,4306 | 1.81 | 0,4649 | 2,28 | 0,4887 | 2,94 | 0,4984 |
| 1,49 | 0.4319 | 1,82 | 0,4656 | 2,30 | 0,4893 | 2,96 | 0,4985 |
| 1.50 | 0,4332 | 1,83 | 0,4664 | 2,32 | 0,4898 | 2.98 | 0,4986 |
| 1,51 | 0,4345 | 1,84 | 0,4671 | 2,34 | 0,4904 | 3,00 | 0,49865 |
| 1.52 | 0,4357 | 1,85 | 0,4678 | 2,36 | 0,4909 | 3,20 | 0,49931 |
| 1.53 | 0,4370 | 1,86 | 0,4686 | 2,38 | 0,4913 | 3.40 | 0,49966 |
| 1.54 | 0,4382 | 1,87 | 0,4693 | 2,40 | 0,4918 | 3,60 | 0,49984 |
| 1,55 | 0,4394 | 1.88 | 0,4699 | 2,42 | 0,4922 | 3,80 | 0,49992 |
| 1.S6 | 0,4406 | 1.89 | 0,4706 | 2,44 | 0,4927 | 4,00 | 0,49996 |
| 1,57 | 0,4418 | 1,90 | 0,4713 | 2,46 | 0,4931 | 4,50 | 0,49999 |
| 1,58 | 0,4429 | 1,91 | 0,4719 | 2,48 | 0,4934 | 5,00 | 0,49999 |
Похожие работы
... проверить знания студента из первой части курса, которая излагается в первых четырёх модулях. Во вторых вопросах билета проверяются знания классической предельной проблемы теории вероятностей и математической статистики, которые излагаются в следующих пяти модулях. 1. Вероятностная модель с не более чем счётным числом элементарных исходов. Пример: испытания с равновозможными исходами. 2. ...
... понятия вероятности задача некоторой несостоятельности классического определения вероятности была решена. Однако наблюдаются попытки дать трактовку вероятности с более широких позиций, в том числе и с позиций теории информации. 2. Динамика развития понятия математического ожидания 2.1 Предпосылки введения понятия математического ожидания Одним из первых приблизился к определению понятия ...
... Вариационные ряды позволяют получить первое представление об изучаемом распределении. Далее необходимо исследовать числовые характеристики распределения (аналогичные характеристикам распределения теории вероятностей): характеристики положения (средняя арифметическая, мода, медиана); характеристики рассеяния (дисперсия, среднее квадратическое отклонение, коэффициент вариации); характеристики ...
... выборок. 5. Исследовательские проекты и их защита. 3 2 1 2 2 2 1 1 1 3 2 1 2 2 Всего 10 5 10 Итого 60 34 Глава 2 Методика обучения школьников основам комбинаторики, теории вероятностей и математической статистики в рамках профильной школы 2.1. Организация при формировании пространственного образа, c использованием ...
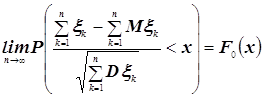

0 комментариев