Навигация
Перевірка статистичних гіпотез відносно невідомих значень параметрів визначеного розподілу
Перевірка статистичних гіпотез відносно невідомих значень параметрів визначеного розподілу
1 Порівняння двох дисперсій нормальних генеральних сукупностей
Ця задача виникає в метрології при порівнянні точності приладів. Крім того, умова рівності дисперсій чи їхньої незмінності в процесі дослідження лежить в основі багатьох задач перевірки гіпотез про порівняння інших параметрів (математичного сподівання, коефіцієнтів кореляції та ін.).
Нехай генеральні сукупності ![]() і
і ![]() розподілені нормально. По незалежних вибірках, узятих з цих сукупностей, з обсягами, які дорівнюють відповідно
розподілені нормально. По незалежних вибірках, узятих з цих сукупностей, з обсягами, які дорівнюють відповідно ![]() і
і ![]() , знайдено виправлені вибіркові дисперсії
, знайдено виправлені вибіркові дисперсії ![]() і
і ![]() . Необхідно за цими характеристиками при заданому рівні значущості
. Необхідно за цими характеристиками при заданому рівні значущості ![]() перевірити нульову гіпотезу про те, що генеральні дисперсії даних сукупностей дорівнюють одна одній:
перевірити нульову гіпотезу про те, що генеральні дисперсії даних сукупностей дорівнюють одна одній:
![]() :
: ![]() .
.
Оскільки виправлені дисперсії є незміщеними оцінками генеральних дисперсій, тобто ![]() ,
, ![]() , нульову гіпотезу можна переписати також у такому вигляді:
, нульову гіпотезу можна переписати також у такому вигляді:
![]() :
: ![]() .
.
У якості критерію перевірки нульової гіпотези про рівність генеральних дисперсій візьмемо відношення виправлених дисперсій, тобто таку випадкову величину:
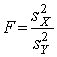 . (1)
. (1)
Можна впевнитися, що величина F за умови справедливості нульової гіпотези має розподіл Снедекора – Фішера (9) з ![]() і
і ![]() ступенями волі.
ступенями волі.
Таким чином, маємо нульову гіпотезу ![]() :
: ![]() і конкуруючу гіпотезу
і конкуруючу гіпотезу ![]() :
: ![]() . У цьому випадку критична область при заданому рівні значимості
. У цьому випадку критична область при заданому рівні значимості ![]() є двосторонньою, обумовленою сукупністю співвідношень:
є двосторонньою, обумовленою сукупністю співвідношень:
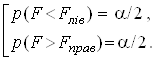 (2)
(2)
Однак, можна показати, що якщо чисельник відносини (1), що визначає випадкову величину ![]() , більше знаменника, тобто якщо
, більше знаменника, тобто якщо ![]() >
>![]() і
і ![]() , то першу нерівність з
, то першу нерівність з ![]() перевіряти не потрібно, тому що вона виконується автоматично при невеликих рівнях значимості
перевіряти не потрібно, тому що вона виконується автоматично при невеликих рівнях значимості ![]() , що звичайно застосовують. При цьому перевірка гіпотези
, що звичайно застосовують. При цьому перевірка гіпотези ![]() зводиться до перевірки тільки другої нерівності з
зводиться до перевірки тільки другої нерівності з ![]() . Це проводиться наступним чином: по таблиці критичних точок розподілу Снедекора – Фишера з
. Це проводиться наступним чином: по таблиці критичних точок розподілу Снедекора – Фишера з ![]() і
і ![]() ступенями волі при вибраному рівні значимості
ступенями волі при вибраному рівні значимості ![]() відповідно (2) знаходять значення величини
відповідно (2) знаходять значення величини ![]() . Далі, якщо
. Далі, якщо 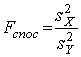 <
<![]() , немає причин відкинути нульову гіпотезу, якщо
, немає причин відкинути нульову гіпотезу, якщо 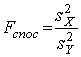 >
>![]() – нульову гіпотезу відкидають.
– нульову гіпотезу відкидають.
Похожие работы
... такому випадку розподіл умовних варіант (3.5) такий: . , , , , . Умовні початкові моменти обчислюються за формулами (3.6): ; ;;; На підставі формул (3.7 – 3.10) при : ; ; ; . 4. Стандартні розподіли математичної статистики 4.1 Розподіл (хі-квадрат) Нехай - система нормальних випадкових величин з одинаковими математичними сподіваннями та середньоквадратичними ...
... , як умови продовження періодичного процесу лактації молока у ВРХ. 1. Система показників статистики тваринництва 1.1 Методологія розрахунку основних показників статистики тваринництва в сегменті великої рогатої худоби (ВРХ) Продукція тваринництва поділяється на дві групи: 1) продукція нормальної життєдіяльності тварин, реалізація якої для вживання за межами тваринництва не пов'язана з ...
... ідження на відміну від маркетингового спостереження передбачають підготовку та проведення різних обстежень, аналіз отриманих даних з конкретної маркетингової завдання, що стоїть перед підприємством. Іншими словами, маркетингові дослідження проводяться періодично, а не постійно, у міру появи певних проблем для агентства, але проводяться постійно для клієнтів агентства. У вищезазначену інформаці ...
... – 266 с. 5. Турчин В.Н. Теория вероятностей и математическая статистика. Учебник. Д.:Изд-во Днепропетр. нац. ун-та, 2008. – 656 с. Додаток А Визначення маркерів компенсованих, субкомпенсованих та декомпенсованих станів за кишкової непрохідності Гемоглобін, еритроцити, кольоровий показник (ступінь насиченості еритроцитів гемоглобіном), Ht, лейкоцити, СОЕ, базофіли, еозиноф ...
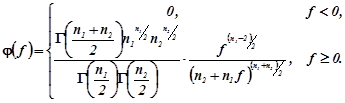
0 комментариев