Порівняння виправленої вибіркової дисперсії з гіпотетичною генеральною дисперсією нормальної сукупності
Порівняння двох середніх довільно розподілених генеральних сукупностей (великі незалежні вибірки)
Порівняння вибіркової середньої з гіпотетичною генеральною середньою нормальної сукупності (при відомій генеральній дисперсії)
Навигация
Порівняння двох середніх довільно розподілених генеральних сукупностей (великі незалежні вибірки)
Перевірка статистичних гіпотез відносно невідомих значень параметрів визначеного розподілу
12607
знаков
0
таблиц
0
изображений
4 Порівняння двох середніх довільно розподілених генеральних сукупностей (великі незалежні вибірки)
У попередній задачі передбачалося, що генеральні сукупності 
і 
розподілені нормально, а їхні дисперсії відомі. Тільки при всіх цих припущеннях у випадку справедливості нульової гіпотези про рівність середніх у незалежних вибірках критерій 
(4) є нормальною нормованою величиною. Під час невиконання хоча б однієї з цих умов метод порівняння середніх, що розроблено під час розв’язання попередньої задачі, є неприйнятним.
Однак, якщо незалежні вибірки мають великий обсяг (
30), можна показати, що вибіркові середні розподілені приблизно нормально, а вибіркові дисперсії 
і 
є досить гарними оцінками генеральних дисперсій, тому їх можна вважати приблизно відомими. Відповідно, критерій
,
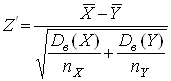що є аналогом критерію (4), має приблизно нормальний розподіл з параметрами 
(за умови справедливості нульової гіпотези) і 
(якщо вибірки незалежні). Тому в цьому випадку можна застосувати метод, розвинутий під час вирішення попередньої задачі, замінивши точний критерій наближеним критерієм 
.
5 Порівняння двох середніх нормальних генеральних сукупностей, дисперсії яких невідомі й однакові (малі незалежні вибірки)
Нехай генеральні сукупності і розподілені нормально, причому їхні дисперсії невідомі. Наприклад, по вибірках малого обсягу не можна одержати гарні оцінки генеральних дисперсій. Тому не можна застосувати метод порівняння середніх, викладений раніше.
Однак якщо додатково припустити, що невідомі генеральні дисперсії є рівними між собою, то можна побудувати критерій (Стьюдента) порівняння середніх. Наприклад, якщо порівнюються середні розміри двох партій деталей, виготовлених на тому ж самому верстаті, то логічно допустити, що дисперсії розмірів, які контролюються, є однаковими.
Якщо ж немає причин вважати, що дисперсії однакові, то, перш ніж порівнювати середні, необхідно за допомогою критерія Снедекора-Фішера (1) попередньо перевірити гіпотезу про рівність генеральних дисперсій.
Далі в припущенні, що генеральні дисперсії однакові, перевіримо нульову гіпотезу 
: 
. Тобто встановимо, значимо чи незначимо розрізняються вибіркові середні 
і 
, що знайдені по незалежних малих вибірках з обсягами 
і 
.
Для перевірки нульової гіпотези у якості критерію застосуємо випадкову величину
,
що, як доведено [5], при справедливості нульової гіпотези має 
-розподіл Стьюдента з 
ступенями волі.
Під час перевірки нульової гіпотези з конкуруючою гіпотезою 
: 
критична область має двосторонній характер. Її будують, виходячи з вимоги, щоб ймовірність влучення критерію Т в цю область у припущенні справедливості нульової гіпотези дорівнювала б прийнятому рівню значущості 
.
Можна показати, що найбільша потужність критерію досягається при рівності ймовірностей влучення критерію в кожний із двох інтервалів критичної області, тобто при
, 
.
Із симетрії -розподілу Стьюдента випливає симетрія і критичних точок, тобто 
. Тому для визначення двосторонньої критичної області досить знайти праву границю 
її області в таблиці критичних точок розподілу Стьюдента при заданому рівні значущості. Зі знайденим таким способом значенням 
зіставимо значення критерію, що спостерігається:
.
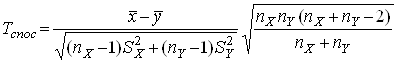Якщо 
, немає причин відкинути нульову гіпотезу, її приймають, у разі 
– нульову гіпотезу відкидають.
Похожие работы
... такому випадку розподіл умовних варіант (3.5) такий: . , , , , . Умовні початкові моменти обчислюються за формулами (3.6): ; ;;; На підставі формул (3.7 – 3.10) при : ; ; ; . 4. Стандартні розподіли математичної статистики 4.1 Розподіл (хі-квадрат) Нехай - система нормальних випадкових величин з одинаковими математичними сподіваннями та середньоквадратичними ...
... , як умови продовження періодичного процесу лактації молока у ВРХ. 1. Система показників статистики тваринництва 1.1 Методологія розрахунку основних показників статистики тваринництва в сегменті великої рогатої худоби (ВРХ) Продукція тваринництва поділяється на дві групи: 1) продукція нормальної життєдіяльності тварин, реалізація якої для вживання за межами тваринництва не пов'язана з ...
... ідження на відміну від маркетингового спостереження передбачають підготовку та проведення різних обстежень, аналіз отриманих даних з конкретної маркетингової завдання, що стоїть перед підприємством. Іншими словами, маркетингові дослідження проводяться періодично, а не постійно, у міру появи певних проблем для агентства, але проводяться постійно для клієнтів агентства. У вищезазначену інформаці ...
... – 266 с. 5. Турчин В.Н. Теория вероятностей и математическая статистика. Учебник. Д.:Изд-во Днепропетр. нац. ун-та, 2008. – 656 с. Додаток А Визначення маркерів компенсованих, субкомпенсованих та декомпенсованих станів за кишкової непрохідності Гемоглобін, еритроцити, кольоровий показник (ступінь насиченості еритроцитів гемоглобіном), Ht, лейкоцити, СОЕ, базофіли, еозиноф ...
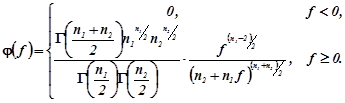
0 комментариев