Порівняння вибіркової середньої з гіпотетичною генеральною середньою нормальної сукупності (при відомій генеральній дисперсії)

6 Порівняння вибіркової середньої з гіпотетичною генеральною середньою нормальної сукупності (при відомій генеральній дисперсії)

Нехай генеральна сукупність  розподілена нормально з дисперсією , причому невідома генеральна середня  приблизно дорівнює значенню .

Потрібно по вибірковій середній , що отримано з вибірки обсягом , при заданому рівні значущості  перевірити нульову гіпотезу :  про рівність генеральної середньої  гіпотетичному значенню . Конкуруючу гіпотезу візьмемо у вигляді: .

З огляду на те, що вибіркова середня є незміщеною оцінкою генеральної середньої, тобто , нульову гіпотезу можна переписати у вигляді: .

У якості критерію перевірки нульової гіпотези візьмемо таку випадкову величину

,

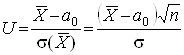яку можна показати, при справедливості нульової гіпотези, є нормованою нормальною величиною.

Далі обчислюємо значення критерію, що спостерігається:

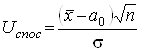 (5)

і по таблиці Лапласа знаходимо критичну точку двосторонньої критичної області зі співвідношення

.

Якщо  – немає причин, щоб відкинути нульову гіпотезу; при  – нульову гіпотезу відкидають.

7 Порівняння вибіркової середньої з гіпотетичною генеральною середньою нормальної сукупності (при невідомій генеральній дисперсії)

У випадку невідомої генеральної дисперсії у якості критерію перевірки нульової гіпотези :  при конкуруючій гіпотезі  приймають випадкову величину

,

де  – "виправлене" середнє квадратичне відхилення. Можна показати, що величина  підкоряється -розподілу Стьюдента з  ступенями волі.

Критична область будується так само, як описано вище. Далі обчислюється значення критерію, що спостерігається:

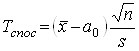 (6)

та по таблиці критичних точок розподілу Стьюдента при заданому рівні значущості  і числі ступенів волі  знаходиться критична точка  у відповідності до умови .

Якщо  – немає причин відкинути нульову гіпотезу і її приймають; при  нульову гіпотезу відкидають.

8 Зв'язок між двосторонньою критичною областю і довірчим інтервалом

Очевидно, що під час побудови двосторонньої критичної області при заданому рівні значущості  попутно визначається і відповідний довірчий інтервал для значень, що приймаються випадковою величиною з надійністю . Перевірка нульової гіпотези :  при :  проводилася на основі умови, що ймовірність влучення критерію 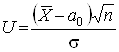 в двосторонню критичну область дорівнювала б рівню значущості , отже, ймовірність влучення критерію в область прийняття гіпотези  дорівнює . Тобто з надійністю  виконується нерівність

,

або рівносильна їй нерівність

, (7)

де  визначається з рівності .

Подвійна нерівність (7) є довірчим інтервалом для оцінки математичного сподівання  нормального розподілу при відомому  із надійністю .

9 Визначення мінімального обсягу вибірки при порівнянні вибіркової і гіпотетичної генеральної середніх

Дуже важливою практичною задачею є визначення мінімального обсягу вибірки, що є необхідним для одержання на її основі обґрунтованих висновків щодо генеральної середньої з наперед заданою точністю  (її смисл – гранична величина різниці між вибірковою і гіпотетичною генеральною середніми).

Наприклад, звичайно потрібно, щоб середній розмір виготовлених деталей відрізнявся від номінального розміру не більше ніж на задану величину . Для проведення контролю з партії виготовлених деталей (генеральна сукупність) відбирається вибірка. Треба з'ясувати, яким має бути мінімальний обсяг цієї вибірки, в якій відсутні браковані деталі, щоб з ймовірністю , де  – рівень значущості, гарантувати, що і в усій партії їх зовсім немає?

Як показано в попередньому пункті, задача визначення довірчого інтервалу для оцінки математичного сподівання нормального розподілу при відомому  і задача відшукання двосторонньої критичної області для перевірки гіпотези про рівність вибіркової середньої гіпотетичній генеральній середній нормальної сукупності зводяться одна до одної. Тому з формули (5) при заміні  на  та  на  випливає, що мінімальний обсяг вибірки має дорівнювати:

 ,

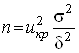де  знаходиться з рівності .

При невідомому  аналогічно скористаємося формулою (6), замінюючи  на . Тоді:

.

Похожие работы

Математична статистика

Скачать

31115

4

3

... такому випадку розподіл умовних варіант (3.5) такий:   . , , , , . Умовні початкові моменти обчислюються за формулами (3.6): ; ;;; На підставі формул (3.7 – 3.10) при : ; ; ; . 4. Стандартні розподіли математичної статистики   4.1 Розподіл (хі-квадрат) Нехай - система нормальних випадкових величин з одинаковими математичними сподіваннями та середньоквадратичними ...

Статистика вивчення продуктивності великої рогатої худоби

Скачать

41584

8

24

... , як умови продовження періодичного процесу лактації молока у ВРХ. 1. Система показників статистики тваринництва   1.1 Методологія розрахунку основних показників статистики тваринництва в сегменті великої рогатої худоби (ВРХ)   Продукція тваринництва поділяється на дві групи: 1) продукція нормальної життєдіяльності тварин, реалізація якої для вживання за межами тваринництва не пов'язана з ...

Маркетингові дослідження на підприємстві

Скачать

137648

4

0

... ідження на відміну від маркетингового спостереження передбачають підготовку та проведення різних обстежень, аналіз отриманих даних з конкретної маркетингової завдання, що стоїть перед підприємством. Іншими словами, маркетингові дослідження проводяться періодично, а не постійно, у міру появи певних проблем для агентства, але проводяться постійно для клієнтів агентства. У вищезазначену інформаці ...

Визначення маркерів компенсованих, субкомпенсованих та декомпенсованих станів за кишкової непрохідності

Скачать

43122

60

40

... – 266 с. 5.                Турчин В.Н. Теория вероятностей и математическая статистика. Учебник. Д.:Изд-во Днепропетр. нац. ун-та, 2008. – 656 с. Додаток А Визначення маркерів компенсованих, субкомпенсованих та декомпенсованих станів за кишкової непрохідності Гемоглобін, еритроцити, кольоровий показник (ступінь насиченості еритроцитів гемоглобіном), Ht, лейкоцити, СОЕ, базофіли, еозиноф ...