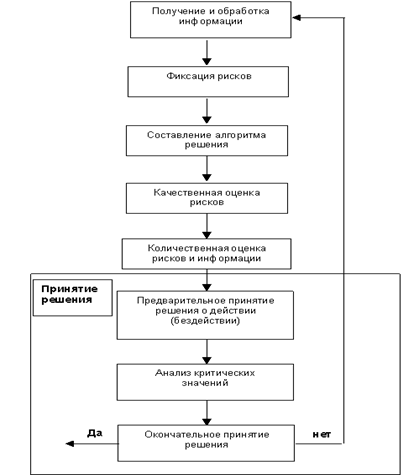
Принятие решений в условиях риска

1. Оценка и выбор многокритериальных решений в условиях определенности

Постановка задачи:

Предприятие (МТЗ) планирует запустить в производство новую модель трактора на базе МТЗ-140.

Заданы семь вариантов (альтернатив) R₁, R₂, R₃, R₄, R₅, R₆, R₇ новых моделей тракторов.

Каждая из семи моделей характеризуется тремя показателями: производительность, себестоимость и надежность.

Требуется:

Используя исходные данные (табл. 1.1), решить задачу многокритериальной оценки, выбора и оптимизации, указанных семи вариантов новых моделей тракторов.

Типы задачи – «Многокритериальная оценка и ранжирование подмножества работоспособных альтернатив (т.е. удовлетворяющих наложенным ограничениям)».

Таблица 1.1 – Исходные данные

№ п/п	Оценочные показатели М	Ограничения	Исходное множество альтернатив Rисх
			R1	R2	R3	R4	R5	R6	R7
			Количественные значения Nr m
1	Производительность	П≥130	135	125	130	140	150	160	120
2	Себестоимость	С≤150	140	170	145	150	135	125	175
3	Надежность	Н≥3300	3400	3500	3550	3200	3600	3700	3150

 

Решение:

Основные этапы алгоритма многокритериальной оценки, выбора и оптимизации альтернатив в условиях определенности:

1.  Задать единицы измерения показателей:

·  производительность трактора – тонн/смена;

·  себестоимость трактора – млн. руб.;

·  надежность трактора – час.

2.  Задать направления экстремизации по каждому показателю:

·  производительность стремится к max,

·  себестоимость – к min;

·  надежность – к min.

3.  Проверить каждую альтернативу на удовлетворение ограничениям:

·  ограничениям не удовлетворяют альтернативы R2, R4, R7;

·  ограничениям удовлетворяют альтернативы R1, R3, R5, R6.

4.  Удалить из исходного множества альтернатив те, которые не удовлетворяют хотя бы одному из ограничений (альтернативы R2, R4, R7).

5.  Формирование подмножеств доминирующих, доминируемых и парето-оптимальных из множества работоспособных альтернатив R_раб:

·  Доминирующие альтернативы (R5, R6);

·  Парето-оптимальные альтернативы (R1, R3).

6.  Определить кванту по каждому  показателю:

·  производительность трактора – 5 т/смена;

·  себестоимость трактора – 30 млн. руб.;

·  надежность трактора – 10 ч.

7.  Проранжировать кванты «сверху – вниз» и «снизу-вверх»:

·  «сверху – вниз»

-   себестоимость;

-   производительность;

-   надежность;

·  «снизу-вверх»

-   надежность

-   производительность

-   себестоимость

8.  Определить весовые коэффициенты  по каждой кванте:

·  производительность трактора – 80;

·  себестоимость трактора – 100;

·  надежность трактора – 55.

9.  Проверить весовые коэффициенты  на соответствие рангам. При обнаружении противоречий между  и рангами, произвести корректировку рангов квант или .

10.  Рассчитать нормированные весовые коэффициенты  для всех квант по формуле:

.

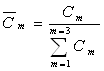·  производительность трактора – 0,34;

·  себестоимость трактора – 0,43;

·  надежность трактора – 0,23.

11.  Рассчитать количество квант  для каждой r-той альтернативы по каждому m-му показателю:

,

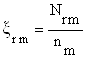где: N_rm – количественные значения каждой r-ой альтернативы по каждому m-му показателю.

Таблица 1.2 – Расчет количества квант

№ п/п	Оценочные показатели М	Ед. изм.	Количество квант ζrm
			R1	R3
1	Производительность	т/смена	27	26
2	Себестоимость	млн. руб.	4,67	4,83
3	Надежность	час	340	355

12.  Построить матрицу мер эффективности  для всех альтернатив по формуле:

.

Таблица 1.3 – Матрица мер эффективности

№ п/п	Оценочные показатели М	Мера эффективности Srm
		R1	R3
1	Производительность	9,19	8,85
2	Себестоимость	1,99	2,06
3	Надежность	79,57	83,09

13.  Рассчитать обобщенный критерий эффективности  для всех альтернатив по формуле:

,

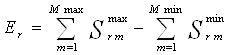где: M_max, M_min – соответственно показатели, подлежащие максимизации и минимизации.

14.  Выбрать узловую  (наилучшую) альтернативу.

Узловой является та альтернатива, которая обладает максимальным значением E_r (с учетом знака), т.е.  (табл. 1.5).

Узловой из парето-оптимальных является альтернатива R3, так как имеет максимальное значение E_r = 89,879.

Таблица 1.4 – Расчет обобщенного коэффициента эффективности

№ п/п	Оценочные показатели М	Обобщенный критерий эффективности Er
		R1	R3
1	Производительность	86,78	89,88
2	Себестоимость
3	Надежность

15.  Определить пути оптимизации .

Узловая альтернатива  подвергается оптимизации следующим образом:

а) Используя матрицу мер эффективности  сформировать упорядоченное множество b_m альтернатив по каждому показателю, исходя из величин  (т.е. выполняется «упорядочение по строкам).

·  производительность <R1, R3>;

·  себестоимость <R1, R3>;

·  надежность <R3, R1>;

б) Определить место узловой альтернативы  в каждом из упорядоченных множеств b_m.

в) Определить возможные пути оптимизации альтернативы  по каждому m-му показателю по правилу: если упорядоченное множество b_m построено по показателю, подлежащему максимизации (соответственно, минимизации), то  может быть улучшена (оптимизирована) за счет использования решений, заложенных в тех альтернативах, которые расположены слева (соответственно, справа) в множестве b_m.

Таблица 1.5 – Матрица исходных данных и результатов расчетов по алгоритму принятия решений в условиях определенности

№ п/п	Оценочные показатели М	Ед. измерения	Ограничения	Направление экстремизации	Исходное множество альтернатив Rисх							Подмножество работоспособных альтернатив Rраб	Величина кванты nm	Ранжирование квант		Весовые коэффициенты квант Cm (0,100)	нормированные Ĉm (0,1)	Количество квант گrm		Мера эффективности Srm		Обобщенный критерий эффективности Er		Выбор Rузл	Пути оптимизации Rузл и анализ их реализации
					R1	R2	R3	R4	R5	R6	R7			"Сверху-вниз"	"Снизу-вверх"
					Количественные значения Nr m													R1	R3	R1	R3	R1	R3
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23		24	25
1	П	т/см.	П≥130	max	135	125	130	140	150	160	120	R1, R3, R5, R6	5	2	2	80	0,34	27	26	9,19	8,85	86,78	89,88	R3	За счет R1
2	С	млн. руб.	С≤150	min	140	170	145	150	135	125	175		30	1	3	100	0,43	4,67	4,83	1,97	2,06				нет
3	Н	час	Н≥3300	max	3400	3500	3550	3200	3600	3700	3150		10	3	1	55	0,23	340	355	79,57	83,09				нет

Вывод:

Для предприятия оптимальным вариантом производства новой модели трактора является модель R6, так как она удовлетворяет всем ограничениям, которые были представлены для анализа.

  2. Оценка и выбор решений в условиях риска

 

Риск – это мера несоответствия между возможными результатами принятого решения и теми результатами, которые могли бы обеспечить оптимальное принятие и реализация оптимального решения.

В хозяйственной деятельности риск может измеряться величиной необходимых дополнительных затрат либо величиной недополученной прибыли.

Источниками риска являются неполнота, недостоверность, неактуальность и неоднозначность используемой информации, как о самой организации, так и о ее внешнем окружении.

Существуют два основных метода определения риска:

1. Статистический, который состоит в накоплении статистических данных об объекте риска (например, о потерях, о прибылях, о работе оборудования, о стабильности трудового коллектива). При достаточно большой базе данных этот метод может дать вполне приемлемые результаты;

2. Метод экспертных оценок, который основан на экспертных оценках специалистов, хорошо знающих анализируемую область хозяйственной деятельности.

Этот метод способен давать хорошие результаты при условии грамотного подбора экспертов (с учетом их компетентности и объективности), а также при достаточной представительности группы экспертов.

Алгоритм анализа риска можно представить как последовательность выполнения следующих этапов:

1.  Выявление возможных рисков во всех направлениях деятельности организации;

2.  Определение вероятности (объективной или субъективной) наступления каждого риска;

3.  Определение тяжести последствий наступления каждого риска. Тяжесть последствий может быть определена несколькими способами:

3.1  В качественной шкале (например, тяжелые последствия, критическое состояние, «легкие ушибы»);

3.2  В баллах, отражающих тяжесть последствий риска;

3.3  В денежном выражении;

3.4  Определение потерь при наступлении каждого риска (произведение вероятности на тяжесть);

3.5  Ранжирование рисков по степени потерь;

3.6  Выбор стратегии и тактики устранения (илиминации) рисков.

Постановка задачи:

Фирма планирует реализацию одного из коммерческих проектов. Причем, известны экспертные оценки, связанные с реализацией этих проектов (см. таблица 2.2).

Требуется:

Выбрать рациональный вариант коммерческого проекта, если среднегодовая прибыль от реализации проекта должна быть не менее 4,5 млн. у.е. при минимальном риске.

Задачу решить по следующей схеме:

·  Оценить эффективность проекта по критерию ожидаемой среднегодовой прибыли;

·  Определить допустимые проекты, исходя из заданного уровня среднегодовой прибыли;

·  Оценить риск допустимых проектов на основе коэффициента вариации ожидаемой среднегодовой прибыли;

·  Из множества допустимых проектов выбрать рациональный вариант коммерческого проекта, которому соответствует минимальный риск.

Таблица 2.1 – Исходные данные

В-т	Оценка	Проект
		1	2	3	4	5	6
18	Пессимистическая оценка Xmin (млн. у.е. в год)	3	3	2	4	2	2
	Оптимистическая оценка Xmax (млн. у.е. в год)	10	8	7	9	8	6

Решение:

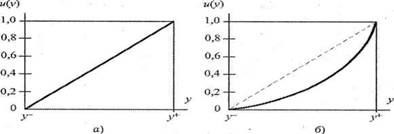
Степень риска коммерческого проекта возможно оценить с помощью коэффициента вариации , который характеризует относительный разброс случайной величины в виде ожидаемой прибыли от реализации проекта:

.

Чем больше коэффициент вариации, тем больше неопределенность в отношении ожидаемой прибыли и, следовательно, тем больше степень риска коммерческого проекта.

Причем принято выделять следующие уровни риска:

Kvar < 10% – малая степень риска;

Kvar = (10-25)% – средняя степень риска;

Kvar > 25% – высокая степень риска.

MO и SIGMA ожидаемой среднегодовой прибыли от реализации коммерческих проектов определяется на основе приближенных соотношений для -распределения.

 

; .

 

1. Оценка эффективность проекта по критерию ожидаемой среднегодовой прибыли.

Проект № 1:

МО = (3*3+2*10)/5 = 5,8.

Проект № 2:

МО = (3*3+2*8)/5 = 5.

Проект№3:

МО = (3*2+2*7)/5 = 4.

Проект №4:

МО = (3*4+2*9)/5 = 6.

Проект №5:

МО = (3*2+2*8)/5 = 4,4.

Проект №6:

МО = (3*2+2*6)/5 = 3,6.

2. Исходя из заданного уровня среднегодовой прибыли (не менее 4,5 млн. у.е.) допустимыми проектами являются проект №1 (МО = 5,8 млн. у.е.), проект №2 (МО = 5 млн. у.е.) и проект №4 (МО = 6 млн. у.е.).

3. Оценка риск допустимых проектов на основе коэффициента вариации ожидаемой среднегодовой прибыли.

 

, .

 

SIGMA₁ = (10-3)/5 = 1,4 млн. у.е.

SIGMA₂ = (8-3)/5 = 1 млн. у.е.

SIGMA₄ = (9-4)/5 = 1 млн. у.е.

₁ = 1,4*100%/5,8 = 24,14 % – средняя степень риска.

₂ = 1*100%/5 = 20% – средняя степень риска.

₄ = 1*100%/6 = 16,7% – средняя степень риска.