Неявні інтерполяційні схеми

6. Неявні інтерполяційні схеми

Алгоритм неявних інтерполяційних методів дослівно повторює алгоритм звичайних (явних) інтерполяційних методів. Єдина відмінність полягає в тому, що ми не використовуємо звичайну (явну) схему Рунге-Кутта другого порядку:

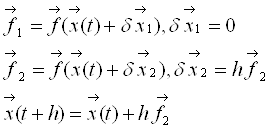
Ми заміняємо її на неявну схему Рунге-Кутта другого порядку:

Нагадаємо, що для цієї схеми можна використовувати два різних рецепта:

•  шукати точне рішення цієї системи нелінійних рівнянь методом Ньютона;

•  обмежитися лінеаризованим рівнянням, тобто зробити тільки перший крок методу Ньютона :

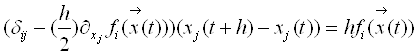
У будь-якому випадку доведеться вирішувати СЛР. В більшості випадків можна обійтись другим варіантом, але в дуже нестійких завданнях доведеться вдатися до першого (до речі, при цьому не доведеться сильно міняти текст програми).

Нагадаємо, що існують варіанти інтерполяційного методу з фіксованим кроком Н і змінним порядком m, з фіксованому порядку те і змінним кроком Н і, нарешті, із змінними m і Н. Тут можна привечти тільки простий алгоритм з фіксованим H.

Алгоритм:

Вибираємо постійний крок H за часом (як правило слід брати H близько 0.2). Рухаємося по траєкторії з цим кроком. Кожен окремий крок реалізується так:

Для k = 1,2,.. виконуємо наступне:

Для чергового N_kз набору {4, 6, 8, 12, 16, 24, 32, 48, 64, 96, 128} обчислюємо крок h_k = H/N_k.

За допомогою цього кроку h_k знаходимо

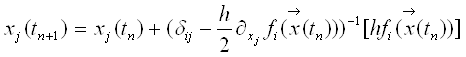
тут t_n = t+nh_k, n = 0.. N_k-1; при цьому . Зрозуміло, тут не слід обчислювати зворотну матрицю, потрібно просто вирішувати СЛР.

Для кожного х_і по k точок:

виконуємо поліноміальну інтерполяцію взалежності Y(X) в точку X = 0. Результат інтерполяції, отриманий на k -му етапі, означаємо . Оцінюємо погрішність

 як

Перетворюємо вектор на число характеризуючи погрішність. Якщо  менше замовленого  те вважаємо  і завершуємо даний крок t→t+H.

Перша неприємна відмінність від явного методу полягає в тому, що кожен маленький крок на h_k (великий крок H складається з N_k штук таких кроків) вимагає рішення СЛР.

Друга неприємна відмінність від явного методу полягає в тому, що тут набагато складніше перетворити вектор  на одне число , оцінюючи погрішність. На жаль, рецепт цього перетворення слідує підібрати залежно від конкретного завдання, тобто від конкретних властивостей "швидких" і "повільних" змінних.

На перший погляд, цей алгоритм приведе не просто до багатьох помилок в описі динаміки "швидких" змінних, а до помилок якісних. Дійсно, якщо рівняння для "швидкої" змінної має вигляд , то при Ch>>1 неявна схема Рунге-Кутта другого порядку замість експоненціального вибуває дає x(t+h)≈-x(t), тобто |x(t+H)|≈|x(t)|. На щастя, наступна інтерполяція виправляє ситуацію. Інтерполяційний алгоритм "помічає", що у міру зменшення h_kабсолютна величина x^(k)(t+H) зменшується. Причому це зменшення тим помітніше, чим менше h_k - В результаті остаточна відповідь  буде помітна менше за абсолютною величиною, чим x(t).

7. Програма Рунге-Кутта на мові С#

Наведемо приклад пограми Рунге-Кутта на мові С#. В програмі використовується абстрактний клас TrungeKutta, в якому потрібно перекрити абстрактний метод F, який задає перші чаcтини рівняння.

using System;

using System.Collections.Generic;

 

namespace rwsh_rk4

{

abstract class TRungeKutta

{

public int N;

double t; // теперішній час

public double[] Y; // шукане число Y[0] – саме рішення, Y[i] - i-та змінна розвязку

double[] YY, Y1, Y2, Y3, Y4; // внутрішня змінна

 

public TRungeKutta(int N) // N – розмір системи

{

this.N = N; // зберегти розміри системи

 

if (N < 1)

{

this.N = -1; // якщо розмірність менше одиниці, то установити флаг помилки

return; // і вийти із конструктора

}

 

Y = new double[N]; // створення вектора розв’язку

YY = new double[N]; // внутрішній розв’язок

Y1 = new double[N];

Y2 = new double[N];

Y3 = new double[N];

Y4 = new double[N];

}

 

public void SetInit(double t0, double[] Y0) // встановлення початкових умов.

{  // t0 – початковий час, Y0 – початкова умова

t = t0;

int i;

for (i = 0; i < N; i++)

{

Y[i] = Y0[i];

}

}

 

public double GetCurrent() // повернути даний час

{

return t;

}

 

abstract public void F(double t, double[] Y, ref double[] FY); // перші частини с-ми.

 

public void NextStep(double dt) // наступний крок метода Рунге-Кутта, dt – крок по часу

{

if(dt<0)

{

return;

}

 

int i;

 

F(t, Y, ref Y1); // вирахувати Y1

 

for (i = 0; i < N; i++)

{

YY[i] = Y[i] + Y1[i] * (dt / 2.0);

}

F(t + dt / 2.0, YY, ref Y2);

 

for (i = 0; i < N; i++)

{

YY[i] = Y[i] + Y2[i] * (dt / 2.0);

}

F(t + dt / 2.0, YY, ref Y3); // вирахувати Y3

 

for (i = 0; i < N; i++)

{

YY[i] = Y[i] + Y3[i] * dt;

}

F(t + dt, YY, ref Y4); // вирахувати Y4

 

for (i = 0; i < N; i++)

{

Y[i] = Y[i] + dt / 6.0 * (Y1[i] + 2.0 * Y2[i] + 2.0 * Y3[i] + Y4[i]); // виразувати р-зок на новому кроці

}

 

t = t + dt; // збільшити крок

 

}

}

 

class TMyRK : TRungeKutta

{

public TMyRK(int aN) : base(aN) { }

 

public override void F(double t, double[] Y, ref double[] FY)

{

FY[0] = Y[1]; // приклад математичний маятник

FY[1] = -Y[0]; // y''(t)+y(t)=0

}

}

 

class Program

{

static void Main(string[] args)

{

TMyRK RK4 = new TMyRK(2);

 

double[] Y0 = {0, 1}; // задаємо початкові умови y(0)=0, y'(0)=1

 

RK4.SetInit(0, Y0);

 

while (RK4.GetCurrent() < 10) // розв’язуєм до 10

{

Console.WriteLine("{0}\t{1}\t{2}", RK4.GetCurrent(), RK4.Y[0], RK4.Y[1]); // вивести t, y, y'

 

RK4.NextStep(0.01); // розв’язати на наступному кроці, крок інтегрування dt=0.01

}

}

}

}