Кинематический анализ рычажного механизма

3. Кинематический анализ рычажного механизма

 

Построение плана скоростей.

План скоростей строим для заданного положения механизма, для φ₁ = 30° (рис. 5). Построение плана скоростей начинаем с ведущего звена (кривошип О₁А), закон движения которого задан. Последовательно переходя от механизма I класса к структурной группе 3 вида, определим скорости всех точек звеньев механизма.

Угловая скорость кривошипа O₁A задана и считается постоянной:

 

ω₁ = 20 рад/с = const.

Линейная скорость точки А кривошипа О₁А

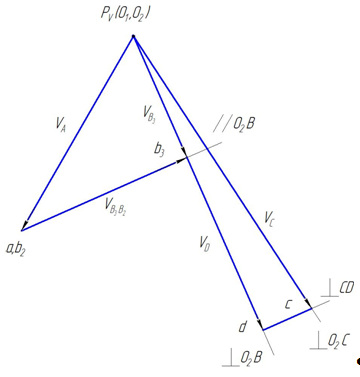
Рис. 6 Построение плана скоростей, µ_v = 0,1 м·с^-1/мм

Из точки Р_v, принятой за полюс плана скоростей откладываем в направлении вращения кривошипа вектор скорости точки А кривошипа О₁А  (рис. 6). Длину вектора линейной скорости точки А, вектор, выбираем произвольно.

Принимаем  = 100 мм, тогда масштабный коэффициент плана скоростей равняется

Чтобы определить скорость точки В кулисы 3, составим векторное уравнение:

,

где  – вектор абсолютной скорости точки В, направленный перпендикулярно О₂В;

 – вектор относительной скорости точки В, направленный параллельно О₂В; .

Получим отрезки, которые изображают на плане скоростей вектор абсолютной скорости точки В –= 59,1 мм и относительной скорости точки В –= 80,7 мм.

Абсолютная скорость точки В:

Относительная скорость точки В:

Для нахождения скорости точки D, принадлежащей кулисе О₂D, восполь-зуемся теоремой подобия

,

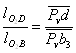откуда определим длину вектора

Отложим на плане скоростей, на векторе, длину вектора .

Абсолютная скорость точки D

Точку c на плане скоростей определим, проведя два вектора скоростей  и , где  – скорость точки C относительно скорости точки D,  – скорость точки C относительно точки О₂. На пересечении этих векторов получим точку с.

Абсолютная скорость точки С:

План скоростей изображен на рис. 6, в принятом масштабе скоростей.

Угловую скорость кулисы 3 находим аналитически по формуле

Построение плана ускорений.

Учитывая, что угловая скорость кривошипа О₁А постоянная , линейное ускорение точки А кривошипа О₁А равняется его нормальному ускорению.

Абсолютное ускорение точки А кривошипа О₁А

От произвольной точки P_a полюса плана ускорения по направлению от А к О₁ откладываем  (рис. 7). Величину отрезка  выбираем произволь-но. Принимаем  = 100 мм.

Масштабный коэффициент плана ускорений

.

Ускорение точки В определим из построения плана ускорений по векторным уравнениям:

,

где  ; - вектор относительного ускорения точки В, направленный параллельно О₂В;

 - вектор кориолисова ускорения.

Отрезок, изображающий на плане кориолисово ускорение:

К_В3В2 ==  · 0,5 = 77 мм,

где  и  - отрезки с плана скоростей, О₂В – отрезок со схемы механизма.

 =  = 0,5

Чтобы определить направление , нужно отрезок , изображающий скорость , повернуть в сторону ω₃ на 90°.

а_В3В2^к = 2 · ω₃ · _B3B2 = 2 · 9,53 · 8,07 = 154 м/с²

Нормальное ускорение при вращении точки В₃ относительно точки О₂ направлено от точки В к точке О₂, а отрезок его изображающий равен:

n_B3О2 =  =  · 0,5 = 28,2 мм

Найдем ускорения из плана ускорений:

 

Для нахождения ускорения точки D, принадлежащей кулисе О₂D, восполь-зуемся теоремой подобия:

,

откуда определим длину вектора

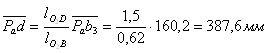
Отложим вектор  на векторе .

Ускорение точки D:

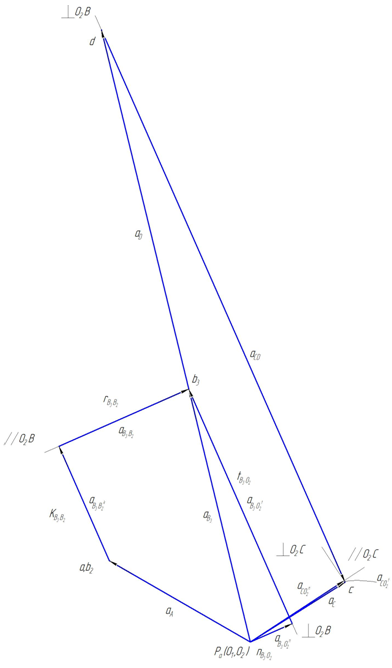
Рис. 7 Построение плана ускорений, µ_а = 2 м·с^-2/мм

Точку c на плане ускорений определим по векторному уравнению:

,

где  вектор относительного ускорения точки С, направленный перпен-дикулярно к вектору;

- вектор относительного нормального ускорения точки С, направленный параллельно СO₂;

- вектор относительного касательного ускорения точки С, направленный перпендикулярно к СO₂.

Нормальное ускорение точки С определим аналитически

,

Отрезок, что изображает вектор нормального ускорения точки С на плане ускорений

.

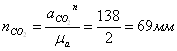шарнирный механизм кулиса кривошип

Абсолютное ускорение точки С

План ускорений изображен на рис. 7, в принятом масштабе ускорений µ_а = 2 м·с^-2/мм.

Угловое ускорение кулисы 3 найдем аналитически

ε₃ =  =  = 508,7 c^-2

Литература

1.  Методические указания к заданиям.

2.  Артоболевский И.И. Теория механизмов и машин. –М.: Наука 1988.

3.  Фролов К.Ф. «Теория механизмов и машин»., под ред. К.Ф.Фролова. – М.: «Высшая школа», 1987.