Навигация
Силовой расчёт рычажного механизма
Содержание
1 Проектирование схемы, структурное и кинематическое исследование рычажного механизма
2 Проектирование неравносмещенной эвольвентной зубчатой передачи и анализ зубчатого механизма
3 Силовой расчет рычажного механизма
4 Расчет маховика
Литература
1. Проектирование схемы, структурное и кинематическое исследование рычажного механизма
Вариант 20 Исходные данные
lOA = 0,2; lAB = 0,6; lСD = 0,2; lВC = 0,5;
w1 = 60π с-1; YС = -0,45 lDЕ = 0,7; XС = -0,22
XЕ = -0,7
Требуется выполнить:
- провести структурный анализ механизма;
- для восьми равноотстоящих (через 45°) положений ведущего звена построить положения остальных звеньев;
- для каждого положения плана механизма построить план скоростей, а для двух положений – план ускорений;
- вычислить линейные скорости и ускорения звеньев механизма.
Результаты вычислений свести в таблицы;
- на планах механизма нанести направления угловых скоростей и ускорений соответствующих звеньев;
1 Структурный анализ механизма
Определяем степень подвижности. Так как механизм плоский, то применяем формулу П.Л. Чебышева
W = 3n – 2P5 – P4,
где n – число подвижных звеньев;
Р4, Р5 – число кинематических пар соответственно четвертого и пятого классов.
n = 5;
P5: O, A, B, C, D,.Е45, Е56;
P4 – нет.
W = 3·5 – 2·7 – 0 = 1.
Это значит, что данная кинематическая цепь является механизмом, в котором достаточно иметь одно ведущее звено.
Для определения класса механизма разбиваем его на структурные группы, у каждой из которых определяем класс, порядок и вид.
![]()

 В
В
![]() А
А
![]() Е С
Е С
![]()
Д
II, 2п, 2в. II, 2п, 1в.

![]() О
О
Ι
Формула строения механизма имеет вид
I (6,1) ® II (2,3) ® II (4,5).
В целом механизм второго класса. Все механизмы второго класса исследуются методом планов.
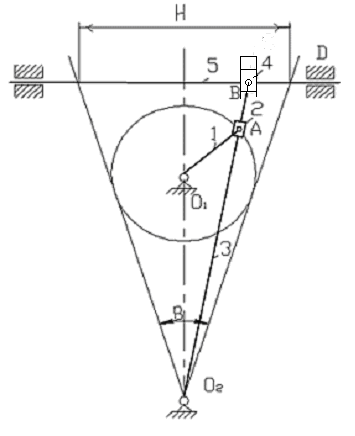
1.1 Построение плана механизма Определяем масштаб для построения плана механизмаml = lOA/OA,
ml = 0,2/20 = 0,01 м/мм.
В принятом масштабе выражаем все остальные геометрические параметры и звенья механизма.
АВ = lAВ/ml = 60 мм, ВС = 50 мм, DЕ = 70 мм, СD = 20 мм,
YС = 45 мм, XС = 22 мм. XЕ = 70 мм.
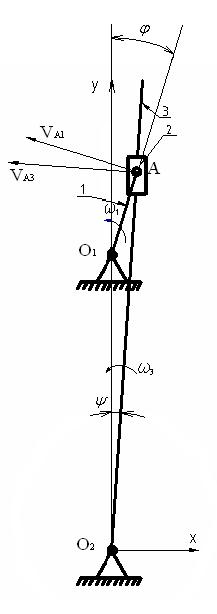
1.2 Построение планов скоростей механизмаПостроение начинаем с определения линейной скорости точки А, принадлежащей ведущему звену ОА.
VA = w1·lOA = 60∙3,14·0,2 = 37,68 м/с.
Направление скорости точки А определится из векторного уравненияVA = VO + VAO, VAO^OA.
Длина отрезка принимается из условия получения «удобного» масштаба mV.
mV = VA/Pа = 37,68/62,8 = 0,6 (м/с)/мм.
Далее строим план скоростей для структурной группы, состоящей из звеньев 2, 3 по уравнению
VB = VA + VBA, VB = Vс + VBС,
где VBA – вектор относительной скорости точки В относительно точки А, направлен перпендикулярно АВ;
VBС – вектор относительной скорости точки В относительно точки С, направлен перпендикулярно ВС;
Проводим из полюса линию перпендикулярную ВС, а из точки а – линию, перпендикулярную звену АВ. В пересечении этих линий найдется точка в.
Скорость точки D определяем по теореме подобия из соотношения
ВС/СD = Pb/Pd => Pd = Pb·CD/BC = 43·20/50 = 17,2 мм.
Скорость т. Е определяем по уравнению:
VЕ =VD+VЕD,
где VЕD – вектор относительной скорости точки Е относительно точки D, направлен перпендикулярно DЕ;
VЕ - вектор абсолютной скорости точки Е, направлен параллельно оси х.
Из плана скоростей определяем линейные скорости точек:
VB = Pb·mV = 43 · 0,6 = 25,8 м/с; VBA = ab·mV = 54 · 0,6 = 32,4 м/с;
VЕD = еd·mV = 10 · 0,6 = 6 м/с; VЕ = Pе ·mV = 19 · 0,6 = 11,4 м/с;
VD = Рd·mV = 17 · 0,6 = 10,2 м/с;
и угловые скорости звеньев
w2 = VBA/lAB = 32,4/0,6 = 54 с-1 , w3 = Vb/lВС = 25,8/0,5 = 51,6 с-1
w4 = VЕD/lDЕ = 6/0,7 = 8,6 с-1 ,
Полученные значения сводим в табл. 1.
Таблица 1 - Значения линейных скоростей точек и угловых скоростей звеньев механизма
| Параметр | Размер-ность | Номера положений | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| VB | м/с | 25,8 | 7,8 | 13,8 | 51,6 | 58,8 | 12,6 | 38,4 | 39 |
| VBA | м/с | 32,4 | 39,6 | 27,6 | 21 | 75,6 | 27 | 3 | 19,8 |
| VЕ | м/с | 11,4 | 3 | 6,6 | 22,8 | 24 | 4,8 | 15,6 | 17,4 |
| VЕД | м/с | 6 | 1,2 | 2,4 | 13,8 | 27 | 6 | 16,2 | 12,6 |
| VД | м/с | 10,2 | 3 | 6 | 20,4 | 23,4 | 4,8 | 15,6 | 15 |
| w2 | с-1 | 54 | 66 | 46 | 35 | 126 | 45 | 5 | 33 |
| w3 | с-1 | 51,6 | 15,6 | 27,6 | 103,2 | 117,6 | 25,2 | 76,8 | 78 |
| w4 | с-1 | 8,6 | 1,7 | 3,4 | 19,7 | 38,6 | 8,6 | 23,1 | 18 |
Направление угловой скорости звена определится, если вектор относительной скорости двух его точек мысленно перенести с плана скоростей на план механизма в точку, стоящую в индексе при скорости на первом месте.
Наносим направления угловых скоростей звеньев на план механизма.
1.3 Построение планов ускорений
Ускорение точки А определяем из векторного уравнения
аА = аО + аАОn + аАОt,
где аО – абсолютное ускорение точки О, м/с², аО = 0, т.к. точка О неподвижна;
аАОn – нормальное ускорение точки А относительно точки О, направлено вдоль звена к центру вращения,
аАОn = w1²·lOA = (60∙3,14)2·0,2 = 7098,9 м/с²
где аАОt - касательное ускорение точки А относительно точки О, аАОt = 0, т.к. w1 = const.
Определяем масштаб плана ускорений
mА = аА/pа = 7098,9/39,44 = 180 (м/с²)/мм,
Для определения ускорения точки В составляем векторное уравнение
аВ = аА + аВАn + аВАt, аВ = аС + аВСn + аВСt,
где аВАn – нормальное ускорение точки В относительно точки А, направлено вдоль звена АВ к точке А, как центру вращения,
аВАn = w22·lАВ = 542·0,6 = 1749,6 м/с2;
аВСn – нормальное ускорение точки В относительно точки С, направлено вдоль звена ВС к точке С, как центру вращения,
аВСn = w32·lВС = 51,62·0,5 = 1331,3 м/с2;
аВАt - касательное ускорение точки В относительно точки А, направлено перпендикулярно нормальному ускорению;
аВСt - касательное ускорение точки В относительно точки С, направлено перпендикулярно нормальному ускорению;
аnВА= аВАn/mА = 1749,6/180 = 9,6 мм. аnВС = аВСn/mА= 1331,3/6,4 = 7,4 мм.
Ускорение точки D определяем по теореме подобия из соотношения
ВС/СD = πb/πd => πd= πb·CD/BC = 22·20/50 = 8,8 мм.
Ускорение т.Е определяем по уравнению:
аЕ = аД + аЕД n + аЕДt
где аЕДn – нормальное ускорение точки Е относительно точки Д, направлено вдоль звена ДЕ к точке Д, как центру вращения,
аЕДn = w42·lДЕ = 8,62·0,7 = 51,7 м/с2;
аЕДt - касательное ускорение точки Е относительно точки Д, направлено перпендикулярно нормальному ускорению
дnЕД = аЕДn/mА = 51,7/180 = 0,29 мм.
Из плана ускорений определяем величины абсолютных ускорений точек и касательных составляющих, которые необходимы для определения угловых ускорений звеньев.
аВ = pb·mА = 22·180 = 3960 м/с2 аД = pd·mА = 9·180 = 1620 м/с2;
aBAt = nBAb·mА = 15·180 = 2700 м/с2; aЕДt = дnЕД·mА = 8·180 = 1440 м/с2;
аЕ = pе·mА = 8·180 = 1440 м/с2 aBСt = nBСb·mА = 21·180 = 3780 м/с2
Определяем угловые ускорения звеньев 2,3 и 4.
e2 = aBAt/lAB = 2700/0,6 = 4500 c-2; e3 = aBCt/lBC = 3780/0,5 = 7560 с-2 ;
e4 = aДЕt/lДЕ = 1440/0,7 = 2057,1 с-2 ;
Для определения направления углового ускорения звена необходимо вектор касательного ускорения мысленно с плана ускорений перенести параллельно самому себе на план механизма в точку, стоящую в индексе при аt на первом месте.
Результаты вычислений заносим в табл. 2.
Аналогично ведем построение планов скоростей и ускорений и их вычисления для всех остальных положений планов механизма.
Таблица 2
Значения линейных ускорений точек и угловых ускорений звеньев механизма
| Параметр | Размер-ность | Номера положений | |
| 1 | 2 | ||
| аB | м/с2 | 3960 | 4500 |
| аτBA | м/с2 | 2700 | 360 |
| аЕ | м/с2 | 1440 | 1980 |
| аτЕД | м/с2 | 1440 | 540 |
| аД | м/с2 | 1620 | 1980 |
| аτBС | м/с2 | 3780 | 4500 |
| ε2 | с-2 | 4500 | 600 |
| ε3 | с-2 | 7560 | 9000 |
| ε4 | с-2 | 2057,1 | 771,4 |
Похожие работы
... 7,41 11,96 12,6 Графические 2,5 ; Диаграммы скоростей и ускорений: Рис.4 - Диаграмма скоростей Рис.5 - Диаграмма ускорений 2. Силовой анализ рычажного механизма Исходные данные: Масса кулисы m3=20 кг; Масса ползуна m5=52 кг; Сила полезного сопротивления Qпс=1550 Н. Схема механизма (Рис.6). ...
... , если к нему приложить уравновешивающую силу и моменты. 2.8 Сравним полученные значения Рур, рассчитанные по методу плана сил и методом рычага Жуковского. Вывод: Проведя силовой анализ механизма, определили реакцию опор, нашли уравновешивающую силу, выяснили, что на данный механизм влияют силы инерции. РАЗДЕЛ III Проектирование эвольвентного зубчатого зацепления Задачами ...
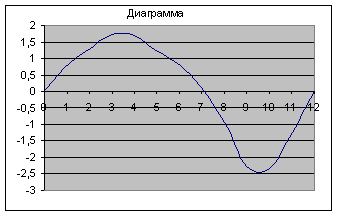
... 1.4 Построение диаграммы перемещений выходного звена. Диаграмма перемещений выходного звена получается в результате построения отрезков, которые берутся с чертежа плоского рычажного механизма в 12 положениях с учётом масштабного коэффициента 1.5 Построение диаграммы скоростей выходного звена. Диаграмма скоростей выходного звена получается в результате графического дифференцирования ...
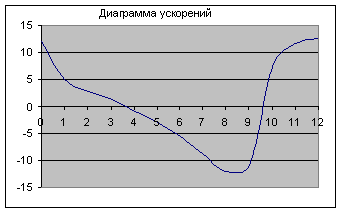
... 24 0,00 0,00 14,10 14,10 9,30 9,30 58,02 58,02 2.4 Исследование механизма методом кинематических диаграмм Исследование механизмов методом диаграмм производится с целями: 1. Получения наглядного представления о законе движения интересующей нас точки или звена механизма. 2. Определения скоростей и ускорений точек или звеньев на основе известного закона перемещений точек или ...



0 комментариев