Знайдемо стани рівноваги системи (2.8). Для цього дорівняємо праві частини системи нулю

1. Знайдемо стани рівноваги системи (2.8). Для цього дорівняємо праві частини системи нулю

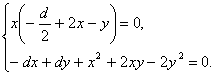
Розглянемо два випадки:

Одержуємо:

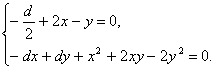
З першого рівняння знайдемо y:

і підставляючи y у друге рівняння одержимо:

Вирішуючи це рівняння, знаходимо:

.

Отже, одержуємо

,

,

Отже, одержуємо крапки

, , ,

і пряму x=0, що є траєкторією системи (2.8).

2. Досліджуємо поводження траєкторій на околицях станів рівноваги

Досліджуємо крапку .

Складемо характеристичне рівняння в крапці .

Звідси

 (2.11)

Отже, характеристичне рівняння прийме вид:

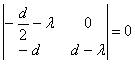
Характеристичними числами для крапки  системи (2.8) будуть , . Коріння  - дійсні й різні знаки не залежно від параметра d, значить крапка  - сідло. Досліджуємо крапку . Згідно (2.11) складемо характеристичне рівняння в крапці :

Характеристичними числами для крапки  системи (2.8) будуть , .

Коріння  - дійсні й одного знака, що залежать від параметра d. Якщо d<0, то крапка  - нестійкий вузол, а якщо d>0, то крапка  - стійкий вузол.

3. Досліджуємо поводження траєкторій в околиці крапки .

Складемо характеристичне рівняння згідно (2.11)

.

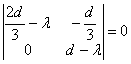Характеристичними числами для крапки  системи (2.8) будуть

,

Коріння  - дійсні й одного знака, що залежать від параметра d. Якщо d<0, то крапка - стійкий вузол, якщо d>0, то крапка  - нестійкий вузол.

4. Досліджуємо поводження траєкторій в околиці крапки .

Згідно (2.11) складемо характеристичне рівняння:

Характеристичними числами для крапки  системи (2.8) будуть , . Коріння  - дійсні й різні знаки не залежно від параметра d, отже  - сідло. Досліджуємо нескінченно - вилучену частину площини системи (2.8) поза кінцями осі oy. Перетворення [7]  переводить систему (2.8) у систему:

 (2.12)

де .

Вивчимо нескінченно - вилучені крапки на осі U, тобто при z=0. Одержуємо:

Отже .

Таким чином, одержуємо дві крапки N1 (0,-1) і N2 (0,1), які є станом рівноваги. Досліджуємо характер цих крапок звичайним способом.

Складемо характеристичне рівняння в крапці N1 (0,-1).

 (2.13), . Маємо:

, .

Коріння  - дійсні й різні за знаком, отже крапка N1 (0,-1) - сідло.

Досліджуємо крапку N2 (0,1). Згідно (2.13) складемо характеристичне рівняння:

, .

Коріння  - дійсні й одного знака, значить крапка N2 (0,1) - стійкий вузол.

Досліджуємо кінці осі y за допомогою перетворення [7] . Це перетворення переводить систему (2.8) у систему:

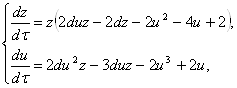 (2.14)

де .

Для дослідження станів рівноваги на кінцях осі y, нам необхідно досліджувати тільки крапку N3 (0,0). Складемо характеристичне рівняння в крапці N3 (0,0):

,

Коріння  - дійсні й одного знака, значить крапка N3 (0,0) - нестійкий вузол.

Тепер дамо розподіл станів рівноваги системи (2.1) у вигляді таблиці 2.

Таблиця 2.

d					∞
					N1	N2	N3
(-∞; 0)	сідло	невуст. вузол	вуст. вузол	сідло	сідло	вуст. вузол	невуст. вузол
(0; +∞)	сідло	вуст. вузол	невуст. вузол	сідло	сідло	вуст. вузол	невуст. вузол

Положення кривих (2.9), (2.10) і розташування щодо їхніх станів рівноваги при d (0 і d (0 дається відповідно мал.2 (а, б).

Поводження траєкторій системи в цілому при d (0 і d (0 дається мал.5 (а, б) додатка Б: Поводження траєкторій системи (2.8).

Питання про існування граничних циклів не виникає, тому що Воробйов А.П. [5] довів, для квадратичної системи граничний цикл не може оточувати вузол.

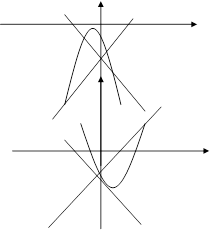
а (d<0) б (d>0)

Мал.2

 

2.3 Дослідження системи (1.1) з коефіцієнтами, заданими формулами (1.52) - (1.53)

Будемо проводити наше дослідження в припущенні, що ,   . Нехай ми маємо систему (1.1), коефіцієнти якої визначаються формулами (1.52) - (1.53). Тоді система (1.1) буде мати вигляд:

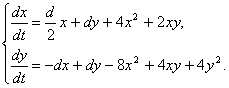 (2.15)

Інтегральні криві в цьому випадку мають вигляд:

 (2.16)

 (2.17)

Тобто приватні інтеграли (1.3) і (1.13) перетворюються в прямі таким чином, що інтегральна крива (2.16) збігається з однієї із прямих інтегральній кривій (2.17).

Знайдемо стани рівноваги системи (2.15). Дорівнявши праві частини системи нулю, і виключивши змінну y, одержимо наступне рівняння для визначення абсцис станів рівноваги:

 (2.18)

З (2.18) одержуємо, що

, , .

Ординати крапок спокою мають вигляд:

, , .

Отже, маємо крапки

, , .

Досліджуємо поводження траєкторій на околицях станів рівноваги .

Досліджуємо стан рівноваги в крапці .

Складемо характеристичне рівняння.

Звідси

 (2.19)

Отже, характеристичне рівняння прийме вид

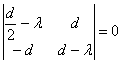
Маємо

,

Або

.

Характеристичними числами для крапки  для системи (2.15) будуть

.

Коріння  - комплексні й залежать від параметра d. Виходить, якщо d<0, то крапка  - стійкий фокус, якщо d>0, то крапка  - нестійкий фокус. Досліджуємо крапку

.

Згідно (2.19) складемо характеристичне рівняння в крапці

.

Маємо

.

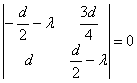Характеристичними числами для крапки  системи (2.15) будуть , . Коріння  - дійсні й різні знаки не залежно від параметра d. Отже, крапка  - сідло.

3. Досліджуємо крапку .

По (2.19) складемо характеристичне рівняння в крапці .

Одержимо

.

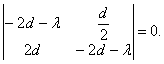
Вирішуючи рівняння, одержимо

,

тобто

,

Коріння  - дійсні й одного знака, що залежать від параметра d. Якщо d<o, то крапка - нестійкий вузол, якщо d>0, то крапка  - стійкий вузол. Досліджуємо нескінченно - вилучену частину площини поза кінцями осі oy перетворенням [7]  Це перетворення систему (2.15) переводить у систему:

 (2.20)

де .

Вивчимо нескінченно - вилучені крапки на осі u, тобто при z=0. Одержуємо

Отже

Отже, маємо дві крапки N1 (0,2) і N2 (0,-2).

Досліджуємо характер цих крапок звичайним способом. Складемо характеристичне рівняння в крапці N1 (0,2).

 (2.21)

.

Отже

, ,

Скористаємося паралельним переносом

 

і підставимо z, u у систему (2.20). Одержимо нову систему:

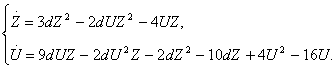 (2.22)

Складемо характеристичне рівняння в крапці N2 (0,-2)

Характеристичними числами для крапки N2 (0,-2), будуть ,  - складний стан рівноваги. Для визначення характеру стану рівноваги скористаємося теоремою [2, с. 196-198]. Теорема 2.1 Нехай крапка (0,0) - ізольований стан рівноваги системи:

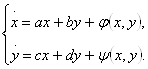 (2.23)

де , є поліноми від x,y починаючи із другого ступеня,  - рішення рівняння , а розкладання функції  має вигляд:

Тоді

1) при m - непарному й m>0 крапка (0,0) - є топологічний вузол;

при m - непарному й m<0 крапка (0,0) - є топологічне сідло;

при m - парному крапка (0,0) є сідло - вузол, тобто такий стан рівноваги, канонічна околиця якого складається з двох гіперболічних секторів. При цьому:

якщо m<0, то усередині гіперболічних секторів укладений відрізок позитивної півосі OX, що примикає до крапки (0,0);

якщо m>0, то відрізок негативної півосі OX.

Щоб скористатися теоремою, необхідно систему (2.22) привести до виду:

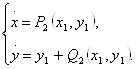
Це можна зробити, скориставшись одним з наступних перетворень [2, с. 199-201]:

якщо ,

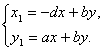
якщо , ,

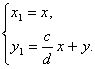
якщо , ,

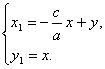
де a, b, c, d - коефіцієнти системи (2.23).

Тоді для системи (2.22) візьмемо наступне перетворення:

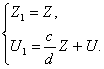
Одержимо

 

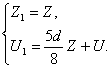
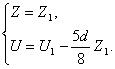
Тоді

 (2.24)

Знайдемо рішення рівняння:

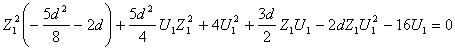
у вигляді ряду по ступенях Z1:

 ,  

Отже

Тоді

Підставляючи U1 у систему (2.24) одержимо:

Звідси

, >0.

Отже, по теоремі 2.1 одержуємо, що крапка N2 (0,-2) - сідло - вузол.

Досліджуємо кінці осі y за допомогою перетворення [7] . Це перетворення переводить систему (2.15) у систему:

 (2.25)

де .

Для дослідження станів рівноваги на кінцях осі y, нам необхідно досліджувати тільки крапку N3 (0,0). Складемо характеристичне рівняння в крапці N3 (0,0)

Відповідно характеристичними числами будуть

Коріння  - дійсні й одного знака. Отже, крапка N3 (0,0) - стійкий вузол.

Тепер дамо розподіл станів рівноваги системи (2.1) у вигляді таблиці 3.

Таблиця 3.

d				∞
				N1	N2	N3
(-∞; 0)	вуст. фокус	сідло	невуст. вузол	сідло	сідло-вузол	вуст. вузол
(0; +∞)	невуст. фокус	сідло	вуст. вузол	сідло	сідло-вузол	вуст. вузол

Положення кривих (2.16), (2.17) і розташування щодо їхніх станів рівноваги при d (0 і d (0 дається відповідно мал.3 (а, б).

Поводження траєкторій системи в цілому при d (0 і d (0 дається мал.6 (а, б) додатка В: Поводження траєкторій системи (2.15).

Питання існування граничних циклів залишається відкритим.

а (d (0)

б (d (0)

Мал.3

Висновок

У даній дипломній роботі побудована квадратична двовимірна стаціонарна система за умови, що приватним інтегралом є крива четвертого порядку, що розпадається на дві криві другого порядку, одна й з яких парабола, друга окружність або гіпербола. При цьому коефіцієнти кривих виражаються через довільний параметр системи.

Список джерел

1. Баутин Н.Н. Про число граничних циклів, що з'являються при зміні коефіцієнтів зі стану рівноваги типу фокуса або центра. - К., 1998

2. Баутин Н.Н., Леонтович Е.А. Методи й прийоми якісного дослідження динамічних систем на площині. - К., 2004

3. Бендиксон І. Про криві, обумовлених диференціальними рівняннями. - К., 2006

4. Биркгоф Дж.Д. Динамічні системи. - К., 2003

5. Воробйов А.П. До питання про цикли навколо особою крапки типу “вузол". - К., 2002

6. Еругин Н.П. Побудова всього множини систем диференціальних рівнянь, що мають задану інтегральну криву. - К., 2003

7. Пуанкаре А. Про криві, обумовлених диференціальними рівняннями. - К., 2004

8. Серебрякова Н.Н. Якісне дослідження однієї системи диференціальних рівнянь теорії коливань. - К., 2005

9. Филипцов В.Ф. До питання алгебраїчних інтегралів однієї системи диференціальних рівнянь. - К., 2003

10. Черкас Л.А. Про алгебраїчні рішення рівняння , де P і Q - багаточлени другого ступеня. - К., 2000

11. Яблонський А.І. Алгебраїчні інтеграли однієї системи диференціальних рівнянь. - К., 2000

Додатки

Додаток А

Поводження траєкторій системи (2.1)

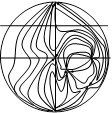
а) (d<0)

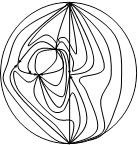
б) (d>0)

Мал.4

Додаток Б

Поводження траєкторій системи (2.8)

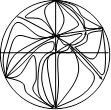
а) (d<0)

б) (d>0)

Мал.5

Додаток В

Поводження траєкторій системи (2.15)

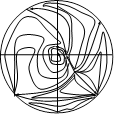
а) (d<0)

б) (d>0)

Мал.6