Содержание
1)Поверхностный интеграл второго рода
2)Вычисление интеграла по поверхности
3)Теорема Остроградского-Гаусса
4)Дивергенция
Литература
интеграл теорема доказательство
Интеграл по поверхности
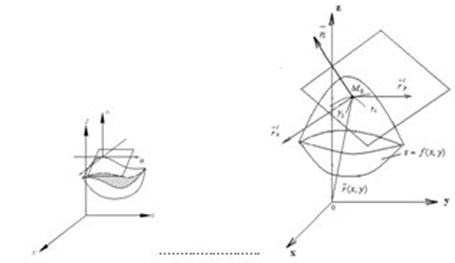
Поверхность будем рассматривать![]()
1. как образ замкнутой области ![]() при непрерывном отображении
при непрерывном отображении ![]()
2. Отображение можно задать в векторном виде ![]() в каждой точке гладкой поверхности
в каждой точке гладкой поверхности ![]()
3. Для ![]() существует нормаль
существует нормаль ![]() , перпендикулярный к касательным
, перпендикулярный к касательным ![]() кривым
кривым ![]() в точке
в точке ![]() . Следовательно
. Следовательно ![]() равен векторному произведению касательных к
равен векторному произведению касательных к ![]() векторов:
векторов:
![]() ,
, 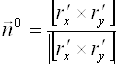
![]()
поверхность ![]()
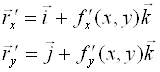 -
-
направление касательных прямых к ![]() и
и ![]() в т.
в т.![]() к поверхности
к поверхности ![]()
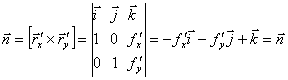
![]()
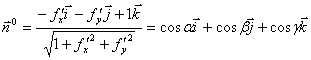 .
.
Направляющие косинусы нормали ![]() к поверхности
к поверхности ![]()
![]()
Задание векторного поля характеризует задание вектор функции:
![]()
Примеры векторных полей:
![]() - поле скоростей текущей жидкости или газа.
- поле скоростей текущей жидкости или газа.
- гравитационное поле
- электростатистическое поле.
Если в какой то области ![]() , заполненной жидкостью (или газом), текущей с некоторой скоростью
, заполненной жидкостью (или газом), текущей с некоторой скоростью ![]() , к каждой точке
, к каждой точке ![]() можно поставить в соответствие векторное поле
можно поставить в соответствие векторное поле ![]() , то получим векторное поле скоростей текущей жидкости.
, то получим векторное поле скоростей текущей жидкости.
Поверхностный интеграл второго рода.
Определение интеграла по поверхности.
Вычисление.
Дано: ![]() - область ограниченная поверхностью
- область ограниченная поверхностью ![]()
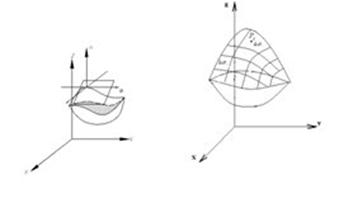
Дано: ![]() - поверхность
- поверхность ![]()
![]()
-векторное поле скоростей текущей жидкости или газа через поверхность ![]() в направлении нормали
в направлении нормали ![]() .
.
Функции ![]() - непрерывны в области
- непрерывны в области ![]() с границей
с границей ![]() .
.
Т/н : поток жидкости (или газа) через поверхность ![]() в направлении
в направлении ![]() .
.
Решение.
1. Поверхность ![]() разобьем на
разобьем на ![]() произвольных частей.
произвольных частей.
![]()
2. Выберем по точке ![]()
![]()
3. Вычислим ![]() скорость течения жидкости в точке
скорость течения жидкости в точке ![]()
4. Определим ![]() , где
, где ![]() -скалярное произведение
-скалярное произведение
![]() -единичная нормаль к поверхности
-единичная нормаль к поверхности ![]() в точке
в точке ![]()
![]() - вектор в точке
- вектор в точке ![]() .
.
5. Составим ![]()
6. Найдем 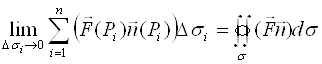
Механический смысл интеграла по поверхности
![]()
![]()
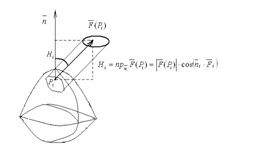
![]() -
-
объем цилиндра с основанием ![]() и высотой
и высотой ![]() .
.
Если ![]() -скорость течения жидкости , то
-скорость течения жидкости , то ![]() равно количеству жидкости или газа протекающий через поверхность
равно количеству жидкости или газа протекающий через поверхность ![]() за единицу времени в направлении нормали
за единицу времени в направлении нормали ![]() .
.
![]() - общее количество жидкости или газа протекающей через поверхность
- общее количество жидкости или газа протекающей через поверхность ![]() в положительном направлении нормали
в положительном направлении нормали ![]() равен потоку векторного поля
равен потоку векторного поля ![]() через поверхность
через поверхность ![]() в направлении нормали
в направлении нормали ![]() .
.
Вычисление интеграла по поверхности
Пусть нормаль ![]() :
:
![]()
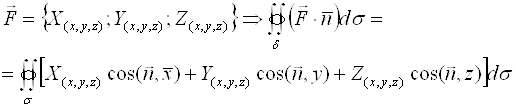
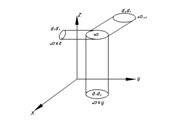
Заметим, что
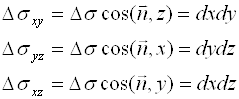
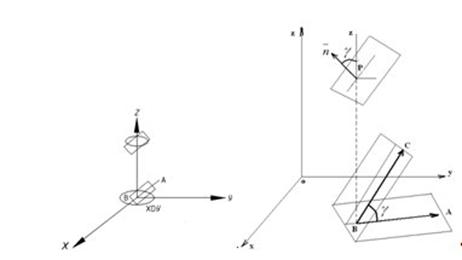
Действительно, ![]() как углы со взаимно перпендикулярными сторонами. Следовательно
как углы со взаимно перпендикулярными сторонами. Следовательно ![]() ,
, ![]() -угол между касательной плоскостью к
-угол между касательной плоскостью к ![]() и его проекцией на плоскость
и его проекцией на плоскость ![]()
Следовательно 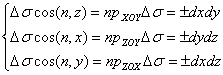
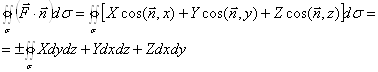
Вычисление интеграла по поверхности.
1. 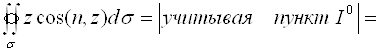
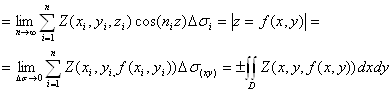
![]()
Аналогично
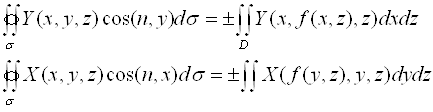
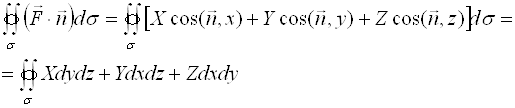
Пример 1.
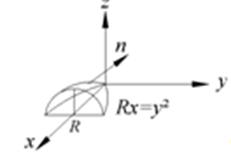
Найти поток вектора ![]() через часть поверхности параболоида
через часть поверхности параболоида
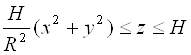 в направлении внутренней нормали.
в направлении внутренней нормали.
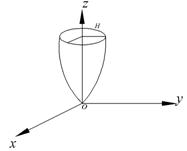
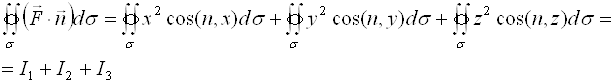
![]() -проектируется на
-проектируется на ![]() с двух сторон и
с двух сторон и ![]() образует с осью Ох углы
образует с осью Ох углы ![]() (острый и тупой )
(острый и тупой ) ![]()
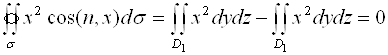
Аналогично
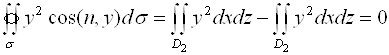

Пример 2. Вычислить ![]() , где
, где ![]() -сфера
-сфера ![]() , нормаль
, нормаль ![]() внешняя.
внешняя.
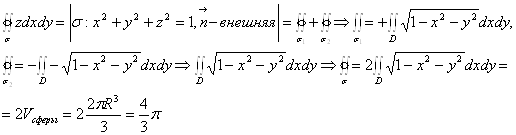
Пример 3. Найти поток вектора ![]() через часть сферы
через часть сферы ![]() в направлении внешней нормали
в направлении внешней нормали
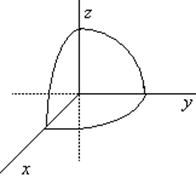

Пример 4. ![]()
![]()
![]()
![]()
Пример 5. ![]()
![]()
![]()
Теорема Остроградского-Гаусса.
Дивергенция.
![]()
![]() -поток вектора через поверхность
-поток вектора через поверхность ![]() в направлении
в направлении ![]() за единицу времени есть разность между количеством жидкости вытекающей из области
за единицу времени есть разность между количеством жидкости вытекающей из области ![]() и количеством жидкости втекающей в область
и количеством жидкости втекающей в область ![]() .
.
1. ![]() . Следовательно из области
. Следовательно из области ![]() жидкости вытекает столько же сколько втекает.
жидкости вытекает столько же сколько втекает.
2. ![]() жидкости или газа вытекает больше, внутри
жидкости или газа вытекает больше, внутри ![]() существует источник.
существует источник.
3. ![]() жидкости или газа втекает больше чем вытекает , внутри
жидкости или газа втекает больше чем вытекает , внутри ![]() существует сток.
существует сток.
Чтобы оценить мощность источников и стоков внутри ![]() нам необходима теорема Остроградского-Гаусса.
нам необходима теорема Остроградского-Гаусса.
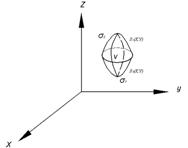
Если ![]() -непрерывна вместе с частными производными в области
-непрерывна вместе с частными производными в области ![]() то:
то:
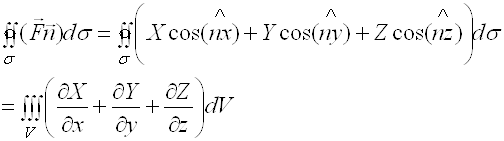
Поток изнутри ![]() равен суммарной мощности источников и стоков в области
равен суммарной мощности источников и стоков в области ![]()
за единицу времени.
Величина потока вектора через замкнутую поверхность ![]() :
:
![]() является глобальной характеристикой векторного поля в области
является глобальной характеристикой векторного поля в области ![]() и очень приблизительно позволяет судить о наличии источников и стоков в области
и очень приблизительно позволяет судить о наличии источников и стоков в области ![]() .
.
· Поток представляет собой избыток жидкости протекающей в сторону положительной нормали ![]() , а не абсолютное количество жидкости прошедшей через
, а не абсолютное количество жидкости прошедшей через ![]() независимо от направления течения. В связи с этим удобно ввести локальную характеристику распределения стоков и источников. Такой характеристикой является дивергенция (плотность потока в точке):
независимо от направления течения. В связи с этим удобно ввести локальную характеристику распределения стоков и источников. Такой характеристикой является дивергенция (плотность потока в точке):
Дивергенция:
Определение: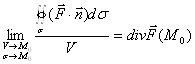
![]() -
- ![]() стягивается в точку.
стягивается в точку.
Определение: Дивергенцией векторного поля ![]() в точке
в точке ![]() называется предел отношения потока векторного поля через поверхность
называется предел отношения потока векторного поля через поверхность ![]() к объему
к объему ![]() , ограниченному этой поверхностью, при условии что поверхность
, ограниченному этой поверхностью, при условии что поверхность ![]() стягивается в точке
стягивается в точке ![]() .
.
Дивергенция характеризует отнесенную к единице объема мощность потока векторного поля ![]() исходящего из точки
исходящего из точки ![]() , т.е. мощность источника и стока
, т.е. мощность источника и стока ![]() находящегося в точке
находящегося в точке ![]() .
.
![]() - средняя объемная мощность потока
- средняя объемная мощность потока ![]() .
.
![]() -существует источник в точке
-существует источник в точке ![]() .
.
![]() - существует сток в точке
- существует сток в точке ![]()
Теорема 2. ![]()
Доказательство: ![]()

![]() ч.т.д.
ч.т.д.
Пример 1. ![]() . Найти поток вектора
. Найти поток вектора ![]() через всю поверхность тела
через всю поверхность тела ![]() ,
, ![]() в направлении внешней нормали.
в направлении внешней нормали.
Решение:
1.![]()
2. 
Литература
1. Ефимов А.В. Математический анализ (специальные разделы). – М. Высшая школа, 1980
2. Ильин В.А., Садовничий В.А., Сендов Б.Х. Математический анализ, I,II ч. М. Издательство МГУ, 1987
3. Шилов Г.Е. Математический анализ функции нескольких вещественных переменных. ч. 1 – 2, М., Наука. Главная редакция физико-математической литературы, 1972.
4. Сборник задач по математике для втузов. Специальные разделы математического анализа I,II ч. М. Наука 1981.
Похожие работы
... (3.3) Дифференцирование ek и fk сводится к дифференцированию uk и vk. 4. Приближенное интегрирование гармонических функций В этом параграфе построим формулы интегрирования произвольной функции из W(S) и базисной последовательности полиномов. Теорема 4.1. Существует единственная последовательность такая, что для любой функции u из W(S) и точки (x0,0) луночки S скалярное ...
льно , где D- проекция на плоскость XOY Пример. , Пример. Определить массу, распределенную на поверхности , плотностью Решение. Специальные векторные поля. 1 Дивергенция. 2 Соленоидальные поля. Свойства. 3 1. Определение дивергенции Теорема Остроградского -Гаусса Пример. Найти поток вектора направленный в отрицательную сторону оси Ох, через ...
... они не требуют от учащихся дополнительных знаний по физике, а, следовательно, удовлетворяют как принципу научности, так и принципу доступности материала. 2.2. Изучение свойств определенного интеграла с помощью физических моделей При изучении интеграла существенным является отбор свойств, которые необходимо знать ученикам. Их должно быть достаточно для рассмотрения приложений интеграла и в ...
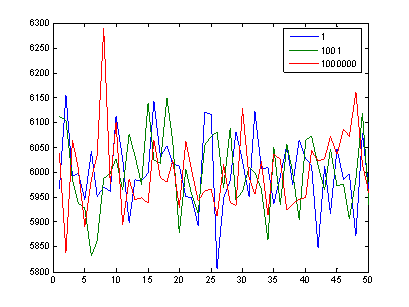
етка – одно из простейших средств получения случайных чисел с хорошим равномерным распределением, на использовании которых основан этот метод. Метод Монте – Карло это статистический метод. Его используют при вычислении сложных интегралов, решении систем алгебраических уравнений высокого порядка, моделировании поведения элементарных частиц, в теориях передачи информации, при исследовании сложных ...
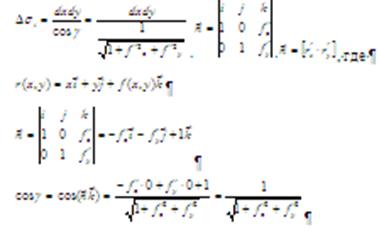

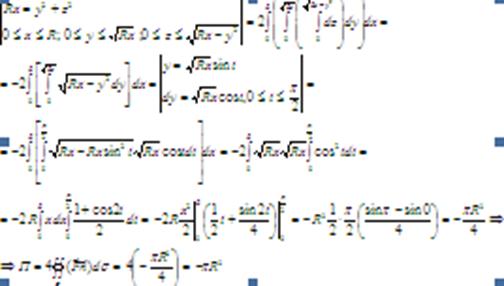

0 комментариев