Навигация
Кубатурные формулы для вычисления интеграла гармонической функции по круговой луночке
С.С. Трахименок, Новосибирский государственный университет, кафедра дифференциальных уравнений
Вычисление интегралов - задача, которая до сих пор интересует как физиков, так и математиков.
В настоящей статье в § 4 предложена формула в виде ряда для вычисления интеграла от гармонической функции по круговой луночке. Эта формула является обобщением теоремы о среднем.
Для того чтобы построить подобное представление в виде ряда, понадобилось ввести (§ 1) некую специальную последовательность гармонических полиномов, которая является базисом пространства типа Бергмана [1]. Введенная последовательность изначально не является ортогональной, поэтому в § 2 предлагаются формулы для вычисления скалярных произведений от базисных функций для того, чтобы применить метод Грама-Шмидта.
1. Области, функциональное пространство, полиномиальные последовательностиОграниченную область S в R2 назовем круговой луночкой, если ее граница Г состоит из двух дуг окружностей Г1 и Г2, пересекающихся в угловых точках С1 и С2. Угол между Г1 и Г2 обозначим через . Введем в R2 декартову систему координат (x,y), поместив ее начало в середину отрезка С1С2, абсолютная величина которого равна 2, и направив ось абсцисс перпендикулярно к нему. С помощью биполярных координат [2]
|
| (1.1) |
круговая луночка S конформно отображается в бесконечную полосу![]() .
.
Обозначив обратное к (1.1) преобразование как =(x,y), =(x,y), отметим, что поверхность (x,y)=j совпадает с Гj. Любая луночка S однозначно определяется заданием 1 и , т.е. S=S(1,). Для произвольной функции u(x,y) суперпозицию u(x(,),y(,)) обозначим как u(,).
В качестве функционального пространства будем рассматривать множество, являющееся подпространством так называемого пространства Бергмана b21, состоящее из гармонических в S функций u(x,y) класса W21(S), обладающих непрерывными следами на частях Г1 и Г2 границы Г. Кроме того, потребуем, чтобы функция fj() u(,j) = u(x,y)Гj , j = 1,2, удовлетворяла на Гj условию Гельдера с показателем d0. Совокупность всех таких элементов u(x,y) обозначим как W(S). Определим в W(S) скалярное произведение, положив:![]() . Здесь (x0,y0) - произвольная внутренняя точка из S.
. Здесь (x0,y0) - произвольная внутренняя точка из S.
Рассмотрим функцию комплексного переменного z = x+iy: ![]() .
.
Функции u0 и v0 принадлежат W0(S) и в биполярных координатах имеют следующий вид:
|
| (1.2) |
Используя формулу [3, (7.117)] с некоторыми дополнительными вычислениями, можно получить интегральные представления:
|
| (1.3) |
Интегралы в (1.3), очевидно, сходятся при a(-,), b2.
Функции u0(,) и v0(,) удовлетворяют условиям Коши-Римана и аналитичны в окрестности любой точки из интервала (0,2). Значит, для такого и вещественного t, удовлетворяющего условию | t | max(, 2-), имеют место разложения:
|
| (1.4) |
Здесь и далее под k понимаются функции uk или vk, k = 0,1,.... Коэффициенты uk(,), vk(,) этих разложений при k1 обладают рядом интересных свойств.
1. Из (1.4) следуют рекуррентные соотношения:
|
| (1.5) |
2. Применим (1.5) к интегралам в (1.3), вычислим полученные равенства по формулам [3, (7.113), (8.108)] и, учитывая (1.1), получим в переменных (x,y):
|
| (1.6) |
3. Соотношения (1.4) в декартовых координатах принимают вид:
|
| (1.7) |
Из (1.6)-(1.7), используя индукцию по k, заключаем, что функции uk(x,y) и vk(x,y) - это гармонические полиномы степени k.
4. Полиномы uk(x,y) четны по y, а vk(x,y) нечетны. Кроме того, при всех k2 в угловых точках полиномы обращаются в нуль.
5. Последовательность {uk,vk}Ґk = 1 полна в W(S) и образует в нем базис.
2. Ортогонализация последовательности полиномов
Последовательность {uk,vk}Ґk = 1 ортогонализуем в скалярном произведении:
|
| (2.1) |
g№0. Для того чтобы эта задача была решена при помощи хорошо известного процесса Грама-Шмидта, необходимо уметь вычислять скалярные произведения вида ![]() ,
, ![]() и
и ![]() . Если воспользуемся формулой Грина, то значения этих скалярных произведений дают следующие формулы:
. Если воспользуемся формулой Грина, то значения этих скалярных произведений дают следующие формулы:
|
|
|
| |
|
|
где =j, j = 1,2. Следовательно, можно ортогонализовать полиномы uk и vk методом Грама-Шмидта в смысле скалярного произведения (2.1). Получившийся базис будем обозначать как {ek,fk}.
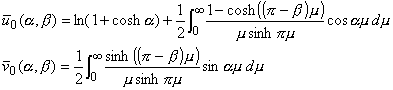
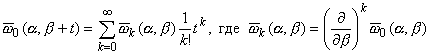
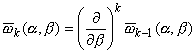
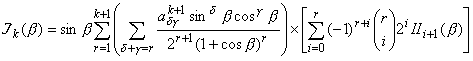
0 комментариев