С каждым объектом данной категории связана специальная стрелка – единичная, или тождественная, стрелка этого объекта

3.  С каждым объектом данной категории связана специальная стрелка – единичная, или тождественная, стрелка этого объекта.

Итак, дадим аксиоматическое определение категории.

Категория Ω включает в себя:

1) Совокупность предметов, называемых Ω - объектами

2) Совокупность предметов, называемых Ω-стрелками

3) Операции, ставящие в соответствие каждой Ω-стрелке f Ω-объект dom f (начало стрелки f) и Ω-объект cod f (конец стрелки f). То, что а=domf и b=cod f изображается так: f: a®b

4) Операцию, ставящую в соответствие каждой паре ‹ g, ¦› Ω-стрелок с dom g=cod f Ω-стрелку g˚¦, композицию f и g, с dom (g˚¦)=dom f и cod(g˚¦)=cod g, причем выполняется следующее условие:

закон ассоциативности:

пусть f: a®b

g: b®c

h: c®d

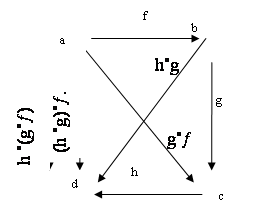тогда h ˚(g˚¦)= (h ˚g)˚¦.

Закон ассоциативности утверждает, что диаграмма вида -

-коммутативна.

( в теории категорий удобным средством являются коммутативные диаграммы. Диаграмма – это схема, в которой указаны объекты и стрелки между ними. При этом, любые два пути, ведущие по стрелкам из одного объекта в другой, равны. Диаграмма называется коммутативной, если есть несколько путей от одного объекта к другому, то все они приводят к одному и тому же результату. Точнее: диаграмма называется коммутативной, когда все возможные треугольники, составляющие части данной диаграммы, коммутативны. Это означает, что любые два пути стрелок данной диаграммы, начинающиеся в одном и том же объекте и заканчивающиеся в одном и том же объекте, задают в композиции одну и ту же функцию. Диаграммы в теории категорий используются для наглядности изложения.)

5) Сопоставление каждому Ω-объекту b Ω-стрелки 1_b: b®b, называемой единичной или тождественной стрелкой, так что выполнен Закон тождества:

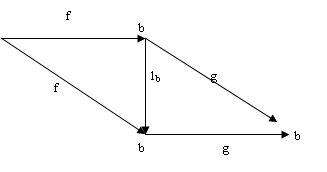для любых Ω-стрелок f:a®b и g:b®c 1_b◦f=f и g◦1_b=g, т.е. коммутативна диаграмма

1.1. Мономорфные стрелки

Определение: Стрелка f:a®b в категории Ω называется мономорфной или монострелкой в Ω, если для любой пары g,h: c®a Ω-стрелок из равенства f °g=f ° h следует g=h.

·  В произвольной категории композиция g°f является монострелкой, если как f, так и g мономорфны.

Доказательство:

Воспользуемся определением монострелки:

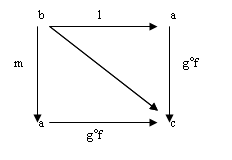
Стрелка g°f:a®c является монострелкой, если для любых стрелок l,m:b®a если (g°f)°l=(g°f)°m, то l=m. Изобразим диаграмму. Очевидно, что требуемое равенство выполняется, т.е. (g°f)°l=(g°f)°m. В любой категории должен выполняться ассоциативный закон. Применяя его, получаем следующее равенство: g°(f°l)=g°(f°m).

 g – монострелка Þ f °l=f °m

f – монострелка Þl=m, что и требовалось доказать.

·  В произвольной категории, если композиция g °f – мономорфна, то и f – мономорфна.

Доказательство: пусть f: a®b

g: b®d,

l, m: c®a

f – мономорфна, если из равенства f °l=f °m (*)следует, что l=m.

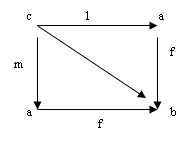Очевидно, что это равенство выполняется.(см. диаграмму). Учитывая, что domg = cod(f °l) = cod(f °m), применим к равенству (*) стрелку g. Получаем g°(f ° l)=g°(f °m). Далее, по ассоциативному закону:

(g°f)°l=(g°f)°m.

g°f – монострелка Þl=m, что и требовалось доказать.

1.2. Эпиморфные стрелки

Определение: Стрелка f:a®b называется эпиморфной или эпистрелкой в категории 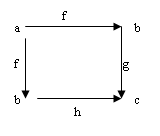Ω, если для произвольной пары стрелок g,h: b®c из равенства g°f=h°f следует g=h, т.е. если коммутативна диаграмма, то g=h.

·  Если g°f-эпистрелка, то g- эпистрелка.

Доказательство: пусть f: a®b

g: b®c,

l, m: c®d

g – эпистрелка, если из равенства l °g=m °g (*)следует, что l=m.

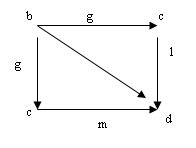
Очевидно, что это равенство выполняется.(см. диаграмму). Учитывая, что codf = dom(l °g) = dom(m °g), применим к равенству (*) стрелку f. Получаем (l ° g)°f=(m ° g)°f. Далее, по ассоциативному закону:

l°(g°f)=m°(g°f).

g°f – эпистрелка Þl=m, что и требовалось доказать.

1.3. Изострелки

Определение: произвольная стрелка f: a®b называется изострелкой или обратимой в категории Ω стрелкой, если существует Ω- стрелка g:b®a, такая, что g°f=1_a и f°g=1_b.  На самом деле такая стрелка только одна. Действительно, если предположить, что существует ещё одна такая стрелка g’, то g’=1_a°g’=(g°f)°g’=g°(f°g’)=g°1_b=g. Стрелка g, когда она существует, называется обратной к f стрелкой и обозначается f ^-1:b®a. Она определяется условиями: f ^-1°f=1_a, f °f ^-1=1_b.

·  Любая изострелка является эпистрелкой.

Доказательство: пусть f: a®b – изострелка, и стрелки g,h: b®c.

Тогда g °f=h °f и существует f ^-1 . Тогда g = g °1_b= g °(f °f^-1) =(ассоциативность)= (g °f) °f^-1 = (h°f)°f^-1=h °(f °f ^-1)=h °1_b=h. Таким образом, f – сократима справа. Ч.т.д.

·  Любая изострелка является монострелкой. (доказательство аналогично предыдущему).

·  Любая изострелка является бистрелкой (эпи и монострелкой ).

Доказательство: следует из предыдущих двух утверждений.

·  Каждая единичная стрелка является изострелкой.

Доказательство: Пусть f: a®a – единичная стрелка. Существует стрелка f ^–1 : a®a и f ^–1 °f=1_a, f °f ^–1=1_a.Þ f – изострелка. Ч.т.д.

·  Если f – изострелка, то f ^–1 – изострелка.

Доказательство: пусть f: a®b – изострелка. Тогда f ^–1: b®a. f – изострелка Þ f °f ^–1=1_b, f ^–1 °f=1_a. Þ f ^–1 – изострелка. Ч.т.д.

·  Если f, g – изострелки, то f °g – изострелка, при этом (f °g)^- 1 = g^–1°f^-1

Доказательство: пусть f: b®c, g: a®b. f °g: a®c. f,g- изострелки Þ $ f ^–1: c®b и $ g ^–1: b®a Þ$ g ^–1°f ^–1 :c®a. Эта композиция является «подозрительной» на обратную к стрелке f °g. Проверим это:

1)  (g ^–1°f ^–1)°(f °g)=(ассоциативность)=g ^–1°(f ^–1°f °g)=g^–1°(1_b°g)=g^–1 °g=1_a.

2)  (f °g )°g ^–1° f ^–1=f °(g °g ^–1°f ^–1)=f °(1_b°f ^–1)=f °f ^–1=1_c.

 Þ f°g- изострелка и (f °g)^-1=g ^–1°f ^–1 .Ч.т.д.