С каждым объектом данной категории связана специальная стрелка – единичная, или тождественная, стрелка этого объекта

3.  С каждым объектом данной категории связана специальная стрелка – единичная, или тождественная, стрелка этого объекта.

2.1. Мономорфизм в категории множеств

·  В категории Set (категория множеств) для любого отображения f:A→B эквивалентны условия:

1)  f- мономорфизм

2)  f-инъекция

3)  g°f=1_A для некоторого g:B→A

Доказательство: поведем по циклу 1)→2)→3)→1)

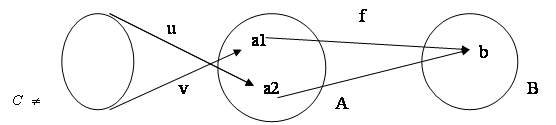1)→2): предположим, что мономорфизм f не является инъективным отображением, т.е.  в А и f(a1)=f(a2)=b.

Возьмем произвольное непустое множество С и два отображения u:C→A, v:C→A, такие, что при отображении v множество С переходит в элемент а1ÎА, а при отображении u множество С переходит в элемент а2ÎА. Заметим, что u¹v. Тогда ,нетрудно видеть, что f°u=b=f°v. но f – мономорфнаÞu=v. Пришли к противоречию, после того, как предположили, что f- не инъективнаÞf – инъективна.

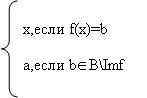2)→3) Пусть f-инъекция. Для доказательства необходимо найти отображение g:B→A. зададим отображение g правилом:

 g(b)=

 

Тогда, очевидно, что g°f=1_A .

3)→1) в произвольной категории доказано свойство о том, что если заданы отображения f:A→B, g:B→A, то из того, что g°f - мономорфизм следует, что f-мономорфизм. По условию g°f=1_А. Выше также доказано свойство о том, что любая единичная стрелка является монострелкой . Из всего вышесказанного следует, что f – мономорфизм. Теорема доказана полностью.

2.2. Эпиморфизм в категории множеств

·  В категории Set (категория множеств) для любого отображения f:A→B эквивалентны условия:

1)  f- эпиморфизм, 2) f-сюръекция, 3) f°g=1_B

для некоторого g:B→A

Доказательство:

доказательство поведем по циклу 1)→2)→3)→1)

1)→2) пусть f – эпиморфизм. Предположим, что отображение f не является отображением «на», т.е. не является сюръекцией. (Imf¹B).

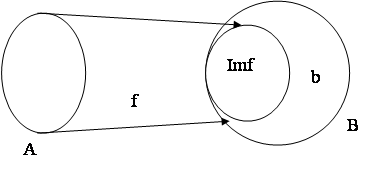Возьмем b1ÎB\Imf.

Пусть С={b1,b2}. Возьмем отображения u:B→C, такое, что любой элемент из В переходит в b2. отображение v:B→C зададим следующим образом:

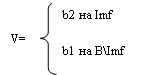
Заметим, что u и v не совпадают. Тогда u°f=b=v°f. Так как f-эпиморфизм (по условию)Þu=v. Получили противоречие после того, как предположили, что f не является сюрьекцией. Значит, f – сюрьекция.

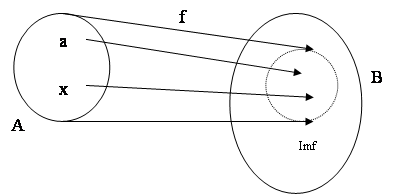
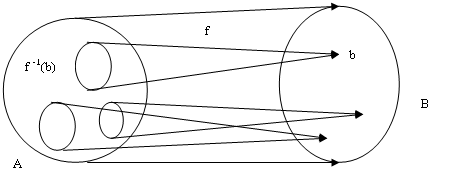2)→3) пусть f- сюрьекция.

сюьективность означает, что  его прообраз не пуст. По аксиоме выбора: существует отображение g:B→. Тогда f °g=1_B. Ч.т.д.

3)→1) в произвольной категории доказано свойство о том, что если заданы отображения f:A→B, g:B→A, то из того, что g°f – эпиморфизм следует, что g-эпиморфизм (док-во см. выше). По условию g°f=1_В. Выше также доказано свойство о том, что любая единичная стрелка является эпистрелкой . Из всего вышесказанного следует, что g – эпиморфизм. Теорема доказана полностью.

Следствие: в категории Set эквивалентны следующие условия: f-бистрелка, f-биекция, f-изоморфизм.

2.3. Начальные и конечные объекты в категории множеств

В категории множеств начальным объектом является пустое множество, так как пустое множество есть подмножество любого множества. Стрелкой можно мыслить пары (элементу одного множества сопоставляется элемент другого). Таким образом, сопоставляя пустому множеству элемент любого множества, получим пустое множество пар, которое является единственным.

Конечными объектами в категории множеств являются одноэлементные множества. Для данного множества А правило f(x)=e определяет функцию f:A→{e}. Так как e является единственным возможным значением, то эта функция является единственной такой функцией. Таким образом, Set имеет много конечных объектов. Все они изоморфны между собой (конечные объекты изоморфны в любой категории). Их представителем является одноэлементное множество {0}.

2.4. Произведение в категории множеств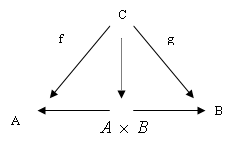

В теории множеств есть понятие прямого произведения множеств. Это такое множество . Существуют естественные отображения – проекции  и , такие, что p_A(a,b)=a , p_B(a,b)=b. Прямое отображение удовлетворяет свойству универсальности: для любых множеств А, В, С и отображений f:C→A и g:C→B существует единственное отображение h: , делающее диаграмму (*) коммутативной.

Легко видеть, что h(c)=(f(c),g(c)). Это свойство универсальности и берется в качестве определения произведения объектов в произвольной категории.

·  В категории Set произведение объектов A и В изоморфно их прямому (декартову) произведению как множеств.

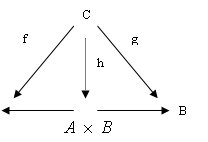Доказательство: с одной стороны мы определили h(c)=(f(c),g(c)). Докажем, что .

Рассмотрим стрелку . Очевидно, что l°h=1_C, h°l=. Следовательно, .

2.5. Копроизведения в категории множеств

В категории Set копроизведение объектов А и В – это их дизъюнктное объединение А+В, т.е. объединение двух множеств, изоморфных А и В соответственно, но не пересекающихся. Точнее, пусть А’={<a,0>:aÎA}=A´{0} и B’={<b,1>:bÎB}=B´{1}. Положим А+В=A'ÈB’. инъекции i_А:А®А+В, i_В:В®А+В определяются правилами i_A(a)=<a,0>, i_B(b)=<b,1> соответственно.

3 Примеры категорий 3.1. Категория 1

Данная категория состоит из одного объекта и одной стрелки. Этим она определяется полностью. Обозначим её единственный объект через а, а её единственную стрелку – через f. Так как в этой категории только один объект, то domf=codf=a, так как по определению категории с каждой стрелкой связано два объекта –её начало и конец. А в данном случае объект только один. У каждого объекта должна быть единичная стрелка. Но так как стрелка f – единственна, то её и берем в качестве единичной. Единственной парой, для которой нужно определить операцию композиции, является пара <f,f> и мы полагаем, что f°f=f. Это дает закон тождества, так как 1_a°f=f°1_a=f°f=f, и закон ассоциативности, так как f°(f°f)=(f°f)°f=f. Так мы определили категорию, которую можно изобразить так:

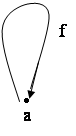
3.2. Категория 2

Эта категория имеет два объекта и три стрелки и выглядит так:

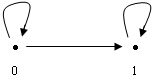в качестве пары объектов возьмем числа 0 и 1, а в качестве стрелок – пары <0,0>, <0,1> и <1,1>. Пусть <0,0>:0®0,

<0,1>:0®1,

<1,1>:1®1.

Тогда <0,0>=1₀ (единичная стрелка на 0) и <1,1>=1₁ (единичная стрелка на 1). При наших требованиях к категориям, композицию на этом множестве можно ввести только одним способом: 1₀°1₀=1₀, <0,1>°1₀=<0,1>, 1₁°<0,1>=<0,1>, 1₁°1₁=1₁. тогда для любых объектов категории выполняется закон тождества и закон ассоциативности.

3.3. Категория 3

Эта категория имеет три объекта и шесть стрелок.

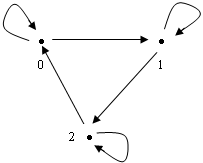объекты: 0,1,2

стрелки: <0,0>, <0,1>, <1,1>, <1,2>, <2,2>, <2,0>.

Стрелки <0,0>,<1,1>,<2,2> - единичные.

Композицию определяем следующим образом:

1₀°1₀=1₀, 1₁°1₁=1₁, 1₂°1₂=1₂, <0,1>°1₀=<0,1>, 1₁°<0,1>=<0,1>, <1,2>°1₁=<1,2>, 1₂°<1,2>=<1,2>, <2,0>°1₂=<2,0>, 1₀°<2,0>=<2,0>. Тогда выполняется закон тождества и закон ассоциативности.

3.4. Категории предпорядка

Категория, в которой любые два объекта p и q связаны не более чем одной стрелкой p®q, называется категорией предпорядка. Если Р – совокупность объектов категории предпорядка, то на ней определено следующее бинарное отношение R: <p,q>ÎRÛ$ p®q. Отношение R обладает следующими свойствами:

2)  рефлексивность (вытекает из того, что для любого объекта категории существует единичная стрелка)

3)  транзитивность (вытекает из того, что стрелка p®q дает в композиции со стрелкой q®s стрелку p®s)

Первые три примера являются и примерами категории предпорядка. Но в них отношение предпорядка удовлетворяет еще свойству антисимметричности, а именно если p®q и q®p, то p=q. Антисимметричное отношение предпорядка называют отношением частичного порядка. Простейшим примером категории предпорядка, 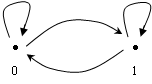но не частичного порядка является двухобъектная категория с четырьмя стрелками: в этой категории существуют стрелки p→q и q→p, но р¹q.

3.5. Дискретные категории

Категория W называется дискретной, если в ней имеются только единичные стрелки, т.е. каждая стрелка является единичной для некоторого объекта. Отождествляя объекты с единичными стрелками, можно заметить, что дискретная категория есть не что иное, как совокупность объектов. Действительно, любое множество X можно превратить в дискретную категорию, добавив единичные стрелки для каждого xÎX.

3.6. Категория N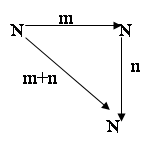

В этой категории ровно один объект, обозначаемый через N. Также категория имеет бесконечную совокупность стрелок из N в N. По определению этими стрелками являются натуральные числа 0,1,2,3… . Каждая стрелка имеет одно и то же начало и конец, а именно единственный объект N. Композиция двух стрелок (чисел) m и n есть снова число. Положим m°n=m+n. Итак, диаграмма коммутативна по определению. Закон ассоциативности для стрелок вытекает из ассоциативности сложения.

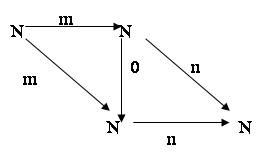Единичная стрелка 1_N объекта N задается числом 0. Диаграмма коммутативна, так как 0+m=m n+0=n.

Литература

1.  Букур И., Деляну А. Введение в теорию категорий и функторов. – М.: Мир, 1972.

2.  Голдблат Р. Топосы. Категорный анализ логики. – М.: Мир, 1983.

3.  Скорняков Л.А. Элементы общей алгебры. – М.: Наука, 1983.

4.  Цаленко М.Ш., Шульгейфер Е.Г. Основы теории категорий. – М.: Наука, 1974.