Навигация
3. Индексы
Под индексами понимают относительный показатель, характеризующий изменение уровня сложного общественного явления во времени и его соотношение в пространстве. Различают индивидуальные и сводные (общие) индексы. Индивидуальный индекс характеризует изменение явления, состоящего из однородных элементов, и представляет собой обычную относительную величину динамики, выполнения плана, сравнения. Индивидуальный индекс обозначаю буквой i с подстрочным указанием индексируемого показателя. Индексируемым называют показатель, изменение которого характеризует индекс. Тек, например, для характеристики выполнения планового задания по производству отдельных видов продукции рассчитывают индивидуальные индексы физического объёма продукции по формуле.
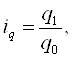
где q1 , q0 – объём производства какого-либо вида продукции в натуральном выражении соответственно в отчётном и базисном периодах, который является индексируемой величиной.
Сводный индекс характеризует изменения явления, состоящего из разнородных непосредственно не суммируемых элементов.
Чтобы охарактеризовать при помощи индексов изменение явлений, состоящих из разнородных элементов, необходимо прежде всего обеспечить возможность суммирования этих элементов для их дальнейшего сопоставления. Для этого следует привести их в соизмеримый вид посредством специального соизмерителя который, являясь общей мерой этих явлений, выражает то общее, что им присуще. Так, для продукции народного хозяйства как совокупности разноимённых видов изделий, несмотря на их различные потребительские свойства, общим является то, что все они представляют собой результат труда, затраты которого могут быть выражены как в единицах рабочего времени, например человеко-часах, так и в стоимостной форме, имеющей денежное выражение. Эти показатели: время, стоимость – могут быть использованы как соизмерители и называются весами индекса. Умножив индексируемый показатель на соответствующий вес, выражаем элементы анализируемой совокупности в одних единицах измерения, т. е. проводим их в соизмеримый вид, поэтому их уже можно суммировать и сопоставлять. Так, например, умножив объём различных видов изделий на их себестоимость, мы выражаем их в стоимостной форме, что позволяет их суммировать и сопоставлять. При этом, чтобы индекс отражал изменение только индексируемой величины, веса индексов берут на одном уровне. Если в качестве веса используются объёмные показатели (продукция, численность), их берут на уровне текущего периода, если качественные показатели (план, себестоимость, затраты времени на единицу продукции), то их принимают на уровне базисного периода.
В статистике широко используются индексы физического объёма продукции, индекс себестоимости, затрат, реализованной продукции, цен, товарооборота, производительности труда, удельного расхода материалов и др.
Сводный индекс физического объёма продукции Iq в общем виде определяется по формуле
Iq= 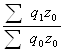 ,
,
где q1 q0 – объём продукции каждого вида изделий соответствующего периода (индексируемый показатель);
z0 – себестоимость каждого вида изделий базисного периода (вес индекса)
Сводный индекс себестоимости Izопределяют по формуле
Iz=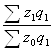 ,
,
где z1 z0 – себестоимость отдельных видов продукции соответственно в текущем и базисном периодах.
Он характеризует, как в среднем изменяется уровень себестоимость продукции различных видов в целом по анализируемой совокупности.
Сводный индекс затрат IZq определяют по формуле
IZq=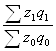 ,
,
где z1q1, z0q0 - затраты по производству различных видов продукции соответственно в отчётном и базисном периодах.
Он характеризует, как изменились затраты по производству продукции различных видов в целом по анализируемой совокупности.
Сводный индекс цен Ip определяют по формуле
Ip=![]() ,
,
где p1 , p0 – цена отдельных видов продукции соответственно в текущем и базисном периодах.
Он характеризует, как изменились в среднем уровни цен на различные виды продукции по анализируемой совокупности.
Сводный индекс товарооборота Iqp определяют по формуле
Iqp=![]()
где q1p1, q0p0 – размер товарооборота соответственно в текущем и базисном периодах.
Сводный индекс производительности труда I1/t определяют по формуле
I1/t=![]() ,
,
где t1, t0 - затраты времени на производство единицы продукции соответственно в текущем и базисном периодах.
Он характеризует изменение производительности труда, является показателем, обратным индексу трудоёмкости It, который определяют по формулам:
It=![]()
I1/t=![]() .
.
Индекс характеризует, как изменились затраты времени на единицу продукции в связи с ростом производительности труда.
Сводный индекс массы отработанного времени Iqt определяют по формуле:
Iqt=![]() ,
,
где q1t1(T1), q0t0(T0) – это время, затраченное на производство всей продукции соответственно в текущем и базисном периодах.
Сводный индекс удельного расхода материалов Im топлива определяют по формуле
Im=![]()
где m1, m0 – удельный расход материалов (топлива), т. е. расход материалов (топлива) на единицу продукции соответственно в текущем и базисном периодах.
Он характеризует, как изменился расход различных видов материалов, топлива на единицу продукции.
Расчёт индексов может быть выполнен в агрегатной форме и форме средних индексов – среднеарифметического взвешенного и среднегармонического. Все вышеприведённые индексы рассчитаны как агрегатные индексы. Выбор формы расчёта индексов зависит от наличия исходных данных. Если известны значения индексируемого показателя и веса в текущем и базисном периодах, то пользуются агрегатной формой индексов. Если отсутствуют значения индексируемого показателя или веса в текущем или базисном периодах, но известны изменения индексируемого показателя или веса по отдельным единицам анализируемой совокупности, пользуются формой средних индексов.
Индекс переменного состава отражает динамику среднего показателя (для однородной совокупности) за счет изменения индексируемой величины х у отдельных элементов и за счет изменения весов f, по которым взвешиваются отдельные значения х. Любой индекс переменного состава – это отношение двух средних величин для однородной совокупности (за два периода или по двум территориям):
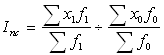 .
.
Индекс фиксированного состава отражает динамику среднего показателя лишь за счет изменения индексируемой величины х, при фиксировании весов на уровне, как правило, отчетного периода f1:
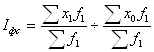 .
.
По аналогии можно показать динамику среднего показателя лишь за счет изменения весов f при фиксировании индексируемой величины на уровне базисного периода х0. такой индекс условно назван индексом структурных сдвигов и имеет вод:
![]() .
.
Индексы широко используются в факторном анализе для выявления меры влияния факторных показателей на средний уровень определяемого или результативного показателя.
Задание 4
Вычислите сводный индекс себестоимости продукции и сумму экономии от снижения себестоимости в абсолютном выражении на основе следующих данных:
Таблица 8
| Наименование изделия | Общая сумма затрат на всю выработку в отчетном году, тыс. руб. | Снижение себестоимости единицы изделия против базисного периода, % |
| А | 120 | 6 |
| Б | 180 | 4 |
Сделайте выводы по результатам расчетов.
Решение
Сводный индекс себестоимости:
![]() или на 4,8%.
или на 4,8%.
В абсолютном выражении:
![]() тыс. руб.
тыс. руб.
Выводы: в среднем себестоимость была снижена на 4.8%, что в абсолютном выражении составило 14,4 тыс. руб.
Похожие работы
... соответственно; q1, q2 - объем отчетного, базисного периодов соответственно) для величины (цены) по каждому виду товара для величины q (объема) по каждому виду товаров: Найдем общие индексы по формулам: представляет собой среднее значение индивидуальных индексов (цены, объема), где j – номер товара. Общий индекс товарооборота равен: Найдем абсолютное ...
... экономико-рыночных отношений в нашей стране ставит перед школой новые задачи. Умение анализировать, сравнивать различные ситуации необходимо на сегодняшний день каждому современному человеку. Элективный курс «Общая теория статистики» с помощью математического аппарата даст начальные понятия о статистике, которые необходимы при решении управленческих задач. Курс рассчитан для учащихся 11 класса ...
0 комментариев