Навигация
4. Выборочное наблюдение
Выборочное наблюдение – это один из видов не сплошного наблюдения, при котором учёту подлежит только часть единиц наблюдаемого явления, и отбор единиц в выборочную совокупность производится по определенному закону. Статистические характеристики, полученные на основе выборочного наблюдения – выборочная средняя, выборочная дисперсия и т. д. всегда отличаются по величине от статистических характеристик генеральной совокупности, охватывающей все единицы изучаемого явления.
Разница статистических характеристик генеральной и выборочной совокупности называется ошибкой выборки или репрезентативности и обозначается
![]()
где xср. генер. и xср. выбор. – соответственно генеральная и выборочная средние.
Величина ошибки выборки средней ![]() зависит от числа наблюдений составляющих выборочную совокупность и дисперсии изучаемого признака
зависит от числа наблюдений составляющих выборочную совокупность и дисперсии изучаемого признака ![]() . Чем больше величина выборки n тем ошибка выборки меньше. Чем больше дисперсия значений признака в выборке
. Чем больше величина выборки n тем ошибка выборки меньше. Чем больше дисперсия значений признака в выборке ![]() тем больше ошибка выборки. Аналитически это записывается так:
тем больше ошибка выборки. Аналитически это записывается так:
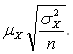
Дисперсию доли, как альтернативного признака, определяют по формуле
![]()
где w – доля
Соответственно ошибка доли определяется по формуле
![]()
В математической статистике доказано, что с определенной вероятностью p можно утверждать, что при данной дисперсии изучаемого признака и числа наблюдений величина ошибки не превысит определённой заранее заданной величины, называемой предельной ошибкой выборки ![]() .
.
Предельную ошибку средней определяют по формуле:
![]()
где t – коэффициент доверия (отношение предельной и средней ошибки выборки).
Коэффициент доверия определяется по выписке из таблицы значений функции приведённую в конце настоящих методических указаний.
Предельную ошибку доли определяют по формуле
![]() .
.
В зависимости от способа отбора единицы в выборочную совокупность различают следующие виды выборки:
индивидуальную, серийную;
случайную, механическую, типологическую;
повторную, бесповторную.
При бесповторной выборке единица изучаемого явления может попасть в выборку только один раз, при повторном способе отбора единица изучаемого явления может попасть в выборку нескольких раз. Соответственно ошибка выборки при бесповторном отборе рассчитывается по формуле:
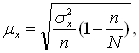
где N – число единиц в генеральной совокупности:
при повторном отборе – по формуле
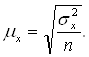
Задаваясь определённой допустимой ошибкой выборки ![]() с вероятностью ошибки p и зная дисперсию изучаемого признака
с вероятностью ошибки p и зная дисперсию изучаемого признака ![]() определяют число единиц n подлежащих отбору в выборочную совокупность при бесповторном отборе:
определяют число единиц n подлежащих отбору в выборочную совокупность при бесповторном отборе:
![]()
при повторном отборе:
![]()
Выписка из таблицы значение функции
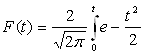
при различных значениях t:
| t | F(t) | t | F(t) | t | F(t) | t | F(t) |
| 0,96 | 0,663 | 1,70 | 0,911 | 1,81 | 0,93 | 1,94 | 0,948 |
| 0,99 | 0,678 | 1,735 | 0,917 | 1,86 | 0,937 | 2,00 | 0,955 |
| 1,46 | 0,856 | 1,75 | 0,92 | 1,90 | 0,943 | 3,00 | 0,997 |
Задание 5
В городе проживает 10 тыс. семей. С помощью выборки предполагается определить долю семей с тремя детьми и более. Какова должна быть численность выборки, чтобы с вероятностью 0,954 ошибка выборки не превышала 0,02, если на основе предыдущих обследований известно, что дисперсия равна 0,2.
Решение
Воспользуемся формулой:
![]() чел.
чел.
Ответ численность выборки должна составлять 1667 человек.
Похожие работы
... соответственно; q1, q2 - объем отчетного, базисного периодов соответственно) для величины (цены) по каждому виду товара для величины q (объема) по каждому виду товаров: Найдем общие индексы по формулам: представляет собой среднее значение индивидуальных индексов (цены, объема), где j – номер товара. Общий индекс товарооборота равен: Найдем абсолютное ...
... экономико-рыночных отношений в нашей стране ставит перед школой новые задачи. Умение анализировать, сравнивать различные ситуации необходимо на сегодняшний день каждому современному человеку. Элективный курс «Общая теория статистики» с помощью математического аппарата даст начальные понятия о статистике, которые необходимы при решении управленческих задач. Курс рассчитан для учащихся 11 класса ...
0 комментариев