Навигация
Относительная величина уровня экономического развития характеризует размеры производства различных видов продукции на душу населения. [4, стр. 4–5]
9. Относительная величина уровня экономического развития характеризует размеры производства различных видов продукции на душу населения. [4, стр. 4–5]
В результате группировки единиц совокупности по величине варьирующего признака получают ряды распределения – первичную характеристику массовой статистической совокупности. Они характеризуют распределение единиц совокупности по какому-либо признаку.
Ряды распределения бывают:
· Атрибутивные (Перечневые) – это ряды, которые имеют характер списка или перечня объектов, по которым учтен изучаемый признак;
· Ранжированные – это ряды, в которых данные наблюдения распределяются по возрастающему или убывающему значению признака;
· Вариационный (интервальный) ряд показывает распределение данных наблюдения в виде интервала по непрерывно изменяющемуся значению признака. [4, стр. 7]
В зависимости от того, какой признак (качественный или количественный) положен в основу группировки, вариационные ряды делятся на дискретные (или прерывные) и интервальные (или непрерывные). Дискретные вариационные ряды основаны на величинах признаков, которые имеют целые значения.
В интервальных вариационных рядах группировочный признак может принимать любое значение (целое, дробное) в пределах каждого интервала. К основным элементам вариационных рядов распределения относятся:
a) варианты (Xi) – это различные значения изучаемого признака;
b) частоты (fi) – это число, показывающее, сколько раз встречается вариант в ряду распределения;
c) частости (Wi) – это отношение частоты данного варианта к сумме всех частот ряда (Wi = fi / S fi).
В таблице N1 приведен ряд распределения числа государственных дневных общеобразовательных учреждений по районам Рязанской области.
На основании приведенных данных построим ряд распределения, для чего определим величину интервала, образовав 5 групп районов области по количеству общеобразовательных дневных учреждений на начало 2008/2009 учебного года:
1 группа – до 15 4 группа – от 35 до 45
2 группа – от 15 до 25 5 группа – свыше 45
3 группа – от 25 до 35
Таблица 1. Распределение государственных дневных общеобразовательных учреждений по районам Рязанской области на начало учебного года
| Рязанская область | 2005/2006 | 2006/2007 | 2007/2008 | 2008/2009 | |||
| 788 | 782 | 772 | 760 | ||||
| 1.г. Рязань | 78 | 78 | 78 | 78 | |||
| 2. г. Касимов | 9 | 9 | 9 | 9 | |||
| 3. г. Скопин | 11 | 11 | 11 | 11 | |||
| 4. г. Сасово | 8 | 8 | 8 | 8 | |||
| Районы области: 5. Ермишенский | |||||||
| 17 | 17 | 16 | 16 | ||||
| 6. Захаровский | 17 | 17 | 17 | 16 | |||
| 7. Кадомский | 18 | 17 | 17 | 17 | |||
| 8. Касимовский | 47 | 47 | 46 | 46 | |||
| 9. Клепиковский | 27 | 26 | 26 | 26 | |||
| 10. Кораблинский | 27 | 27 | 26 | 26 | |||
| 11. Милославский | 27 | 27 | 24 | 23 | |||
| 12. Михайловский | 35 | 35 | 34 | 34 | |||
| 13. Новодеревенский | 26 | 26 | 26 | 26 | |||
| 14. Пителенский | 15 | 15 | 15 | 15 | |||
| 15. Пронский | 26 | 26 | 26 | 26 | |||
| 16. Путятинский | 16 | 16 | 16 | 16 | |||
| 17. Рыбновский | 31 | 31 | 31 | 29 | |||
| 18. Ряжский | 24 | 22 | 21 | 21 | |||
| 19. Рязанский | 41 | 41 | 41 | 41 | |||
| 20. Сапожковский | 18 | 17 | 17 | 17 | |||
| 21. Сараевский | 36 | 36 | 36 | 36 | |||
| 22. Сасовский | 32 | 31 | 31 | 30 | |||
| 23. Скопинский | 37 | 38 | 37 | 36 | |||
| 24. Спасский | 37 | 37 | 37 | 37 | |||
| 25. Сторожиловский | 19 | 19 | 19 | 19 | |||
| 26. Ухоловский | 16 | 16 | 15 | 15 | |||
| 27. Чучковский | 17 | 17 | 17 | 17 | |||
| 28. Шацкий | 42 | 41 | 41 | 38 | |||
| 29. Шиловский | 34 | 34 | 34 | 34 | |||
Группировка – это расчленение совокупности на группы по определенным признакам.
Группировочные признаки могут быть: атрибутивные, количественные, признаки времени.
Группировочный признак – это признак, по которому происходит объединение отдельных единиц совокупности в однородные группы.
На основании полученных границ интервалов построим итоговую группировочную таблицу 2.
Таблица 2. Распределение районов Рязанской области по количеству общеобразовательных дневных учреждений на начало 2008/2009 учебного года
| Группы районов по количеству ГОУ х | Число районов в группе f | Общее количество общеобразовательных учреждений Рязанской области |
| До 15 | 5 | 58 |
| От 15 до 25 | 9 | 162 |
| От 25 до 35 | 8 | 228 |
| От 35 до 45 | 5 | 188 |
| Свыше 45 | 2 | 124 |
| Всего: | 29 | 760 |
Статистическая совокупность всегда структурирована и имеет определенные составляющие. Относительная величина структуры характеризует состав, структуру совокупности по тому или иному признаку и показывает вклад составляющих совокупности в общую массу. Они определяются отношением размеров составных частей совокупности к общему итогу. Структура государственных дневных общеобразовательных учреждений приведена в таблице 3.
Таблица 3. Структура государственных общеобразовательных учреждений Рязанской области на начало учебного года
| Годы | Число общеобразовательных учреждений – всего | В том числе | |||||||||||||||
| начальных | основных | средних (полных) | Для детей с ограниченными возможностями здоровья | ||||||||||||||
| Кол-во | % | Кол-во | % | Кол-во | % | Кол-во | % | Кол-во | % | ||||||||
| всего | |||||||||||||||||
| 2002/2003 | 807 | 100,0 | 180 | 22,3 | 294 | 36,4 | 318 | 39,4 | 15 | 1,9 | |||||||
| 2003/2004 | 797 | 100,0 | 171 | 21,5 | 292 | 36,6 | 319 | 40,0 | 15 | 1,9 | |||||||
| 2004/2005 | 791 | 100,0 | 170 | 21,5 | 285 | 36,0 | 321 | 40,6 | 15 | 1,9 | |||||||
| 2005/2006 | 788 | 100,0 | 171 | 21,7 | 280 | 35,5 | 323 | 41,0 | 14 | 1,8 | |||||||
| 2006/2007 | 782 | 100,0 | 170 | 21,7 | 274 | 35,0 | 324 | 41,4 | 14 | 1,9 | |||||||
| 2007/2008 | 772 | 100,0 | 168 | 21,8 | 264 | 34,2 | 326 | 42,2 | 14 | 1,8 | |||||||
| 2008/2009 | 760 | 100,0 | 159 | 20,9 | 261 | 34,3 | 326 | 42,9 | 14 | 1,9 | |||||||
| Городская местность | |||||||||||||||||
| 2002/2003 | 186 | 23,0 | 12 | 6,5 | 24 | 12,8 | 138 | 74,2 | 12 | 6,5 | |||||||
| 2003/2004 | 187 | 23,5 | 12 | 6,4 | 25 | 13,4 | 138 | 73,8 | 12 | 6,4 | |||||||
| 2004/2005 | 186 | 23,5 | 12 | 6,5 | 24 | 12,9 | 138 | 74,2 | 12 | 6,4 | |||||||
| 2005/2006 | 186 | 23,6 | 12 | 6,5 | 25 | 13,4 | 139 | 74,7 | 10 | 5,4 | |||||||
| 2006/2007 | 186 | 23,8 | 12 | 6,5 | 25 | 13,4 | 139 | 74,7 | 10 | 5,4 | |||||||
| 2007/2008 | 185 | 24,0 | 12 | 6,5 | 23 | 12,4 | 140 | 75,7 | 10 | 5,4 | |||||||
| 2008/2009 | 183 | 24,0 | 10 | 5,5 | 23 | 12,6 | 140 | 76,5 | 10 | 5,4 | |||||||
| Сельская местность | |||||||||||||||||
| 2002/2003 | 621 | 77,0 | 168 | 27,1 | 270 | 43,5 | 180 | 29,0 | 3 | 0,4 | |||||||
| 2003/2004 | 610 | 76,5 | 159 | 26,1 | 267 | 43,8 | 181 | 29,7 | 3 | 0,4 | |||||||
| 2004/2005 | 605 | 76,5 | 158 | 26,1 | 261 | 43,1 | 183 | 30,2 | 3 | 0,4 | |||||||
| 2005/2006 | 602 | 76,4 | 159 | 26,4 | 255 | 42,4 | 184 | 30,6 | 4 | 0,6 | |||||||
| 2006/2007 | 596 | 76,2 | 158 | 26,5 | 249 | 41,8 | 185 | 31,0 | 4 | 0,7 | |||||||
| 2007/2008 | 587 | 76,0 | 156 | 26,6 | 241 | 41,0 | 186 | 31,7 | 4 | 0,7 | |||||||
| 2008/2009 | 577 | 76,0 | 149 | 25,8 | 238 | 41,2 | 186 | 32,2 | 4 | 0,8 | |||||||
Нагляднее структуру явления характеризуют секторные диаграммы (Рис. 1,2).
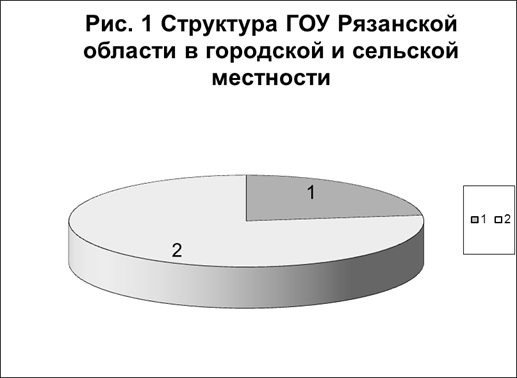
1 – городская местность; 2 – сельская местность
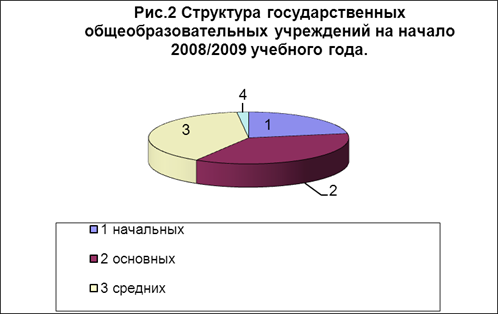
2. Средние показатели и показатели вариации образования в Рязанской области
Чтобы охарактеризовать статистическую совокупность в целом, часто пользуются средней величиной, одной из важнейших характеристик вариационного ряда.
Средняя величина – это обобщающая характеристика однородной совокупности явлений по определенному признаку.
Метод средних величин заключается в замене индивидуальных значений признака единиц наблюдений, то есть в замене X1, X2, X3…Xn некоторой величиной ![]() .
.
В зависимости от характера признака, который усредняется и наличия исходной статистической информации в статистике используют следующие виды средних:
· средняя арифметическая;
· средняя гармоническая
· средняя квадратическая;
· средняя геометрическая.
Каждая их отмеченных видов средних может выступать в двух формах: простой и взвешенной. Простая средняя применяется при вычислении средней по первичным данным, взвешенная – по сгруппированным данным.
Самым распространенным видом средней, применяемой в социально-экономическом анализе, является средняя арифметическая. Средняя арифметическая простая применяется в тех случаях, когда каждое индивидуальное значение признака встречается одинаковое количество раз, то есть когда средняя рассчитывается по группированным единицам совокупности. Но чаще бывает так, что отдельные значения исследуемой совокупности встречаются не один, а много, причем неодинаковое число раз, то есть представляет собой ряд распределения.
В этих случаях рассчитывают среднюю арифметическую взвешенную.
Формулы средней арифметической:
простой- ![]() взвешенной-
взвешенной-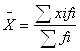
![]() Для определения средней арифметической необходимо иметь ряд вариантов и частот, то есть значения x и f. В некоторых случаях известны индивидуальные значения x и произведение xf, а частоты f неизвестны. Чтобы рассчитать среднюю, обозначим произведение w = x*f, отсюда:
Для определения средней арифметической необходимо иметь ряд вариантов и частот, то есть значения x и f. В некоторых случаях известны индивидуальные значения x и произведение xf, а частоты f неизвестны. Чтобы рассчитать среднюю, обозначим произведение w = x*f, отсюда:
![]()
Теперь преобразуем формулу средней арифметической таким образом, чтобы по имеющимся данным x и w исчислить среднюю. Выразим в формуле средней арифметической f через x и w и получим:
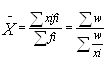
Средняя в такой форме называется средней гармонической взвешенной.
Средняя геометрическая равна корню степени n из произведения коэффициентов роста, характеризующих отношение величины каждого последующего периода к величине предыдущего.
Формула средней геометрической имеет вид:
![]()
Среднюю арифметическую применяют тогда, когда объем совокупности формируется не суммой, а произведением индивидуальных значений признаков.
В тех случаях, когда осреднению подлежат величины, выраженные в виде квадратных функций, применяется средняя квадратическая. Средняя квадратическая рассчитывается по формуле:
простая – 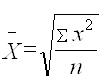 ; взвешенная –
; взвешенная – 
![]()
Для характеристики величины варьирующего признака пользуются так называемыми структурными средними – модой и медианой. Величина моды и медианы, как правило, отличается от средней величины, совпадая с ней только в случае симметрии вариационного ряда.
Мода (M0) – это значение признака, которое наиболее часто встречается в ряду распределения. Способ вычисления моды зависит от вида статистического ряда. Для атрибутивных и дискретных рядов распределения моду определяют визуально, без расчетов по значению варианта с наибольшей частотой.
В интервальном ряду сначала определяется модальный интервал (интервал с наибольшей частотой) и значение моды в середине интервала рассчитывается по формуле:
M0 = X0+h*____fm– fm-1
(fm– fm-1) + (fm– fm+1), где:
X0 – нижняя граница модального интервала;
h – величина модального интервала;
fm-1, fm, fm+1 – частота соответственно домодального, модального и послемодального интервала.
Медианой (Mе) в статистике называют такое значение варьирующего признака, которое делит ряд распределения на две равные части по объему частот или частностей. [4, стр. 11] Медиана для интервального ряда вычисляется для середины медианного интервала, за который принимается такой интервал, где сумма накопленных частот превышает половину значений частот ряда распределения. В данном случае для расчета медианы применяют формулу:
Mе = X0+h*__ЅSf– Sm-1
fm, где:
X0 – нижняя граница медианного интервала;
h – величина медианного интервала;
ЅSf – половина суммы накопленных частот ряда распределения;
Sm-1 – сумма накопленной частоты интервала, предшествующего медианному;
fm – частота медианного интервала.
Медиана не зависит от амплитуды колебания ряда, от распределения частот в пределах двух равных частей ряда, поэтому ее применение позволяет получить более точные расчеты, чем при использовании других форм средних.
По данным ряда распределения таблица N4 определим структурные средние.
Таблица 4. Распределение районов Рязанской области по количеству общеобразовательных дневных учреждений на начало 2008/2009 учебного года
| Группы районов по количеству ГОУ х | Число районов в группе f | X¢ | Xf | Накопленные частоты fm |
| До 15 | 5 | 10 | 50 | 5 |
| От 15 до 25 | 9 | 20 | 180 | 14 |
| От 25 до 35 | 8 | 30 | 240 | 22 |
| От 35 до 45 | 5 | 40 | 200 | 27 |
| Свыше 45 | 2 | 50 | 100 | 29 |
| Всего: | 29 |
| 770 |
|
M0 = 15+10*![]() = 15+10*0,8 = 23
= 15+10*0,8 = 23
Mе = 25 + 10*14,5–14 = 25+10*0,0625 = 25,6 »26
Полученные таким образом расчеты средней и структурных средних свидетельствуют о том, что наиболее часто в Рязанской области встречаются районы с числом дневных общеобразовательных учреждений равным 23. Однако более половины районов области имеют 26 общеобразовательных учреждений, при среднем количестве общеобразовательных заведений в районах 27.
При изучении явлений и процессов общественной жизни статистика встречается с разнообразной вариацией признаков, характеризующих отдельные единицы совокупности. Величины признаков изменяются под действием различных факторов. Очевидно, чем разнообразнее условия, влияющие на размер данного признака, тем больше его вариация.
При характеристике колеблемости признака применяют систему абсолютных и относительных показателей.
К абсолютным показателям вариации относят:
· размах вариации R = x max – x min;
· среднее линейное отклонение 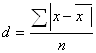
· дисперсия s2 = 
· среднеквадратическое отклонение s =![]() .
.
Эти показатели (кроме дисперсии) измеряются в тех же единицах, что и сам признак: в тоннах, метрах, секундах, рублях. К относительным показателям вариации относятся:
· коэффициент осцилляции Косу = ![]()
![]()
· Линейный коэффициент вариации Kл..вар = ![]()
· Коэффициент вариации V = ![]()
Эти показатели выражаются в процентах или коэффициентах.
Наиболее простым способом измерения колеблемости является определение размаха вариации, то есть разности между максимальным и минимальным значениями признака. Величина R показывает, в каких пределах колеблется размер признака, образующего ряд распределения. Показатель R выражается в тех же единицах измерения, что и варианты признака. Но размах вариации, как показатель колеблемости имеет существенный недостаток. Его величина определяется крайними значениями признака, в то время как колеблемость последнего в целом складывается из суммы всех значений. Поэтому размах вариации может в ряде случаев неправильно характеризовать колеблемость признака.
В статистическом анализе вариации имеет большое значение дисперсия (s2). Однако ее применение как мера вариации в ряде случаев бывает не совсем удобным, потому что размерность дисперсии равна квадрату размерности изучаемого признака. В таких случаях для измерения вариации признака вычисляют среднеквадратическое отклонение.
Дисперсия и среднеквадратическое отклонение недостаточно полно характеризуют колеблемость признака, так как показывают абсолютный размер отклонений, что затрудняет сравнение изменчивости различных признаков.
Для характеристики колеблемости явлений среднеквадратическое отклонение сопоставляют с его средней величиной и выражают в процентах. такой показатель называют коэффициентом вариации и рассчитывают по формуле:
![]() .
.
По величине коэффициента вариации можно судить о степени вариации признаков совокупности. Чем больше его величина, тем больше разброс значений вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя.
Вычислим показатели вариации, для чего используем данные табл. 5.
Таблица 5. Расчетные значения показателей вариации
| X | f | (x – | (x – | (x – |
| 10 | 5 | -17 | 289 | 1445 |
| 20 | 9 | -7 | 49 | 441 |
| 30 | 8 | 3 | 9 | 72 |
| 40 | 5 | 13 | 169 | 845 |
| 50 | 2 | 23 | 529 | 1058 |
| 150 | 29 | x | x | 3861 |
s2 = 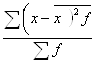 =
= ![]() = 133,1
= 133,1
s = ![]() = 11,5
= 11,5
Коэффициент вариации:
Vs =![]() * 100% =
* 100% = ![]() * 100% = 42,7%
* 100% = 42,7%
Среднеквадратическое отклонение показывает, что число общеобразовательных учреждений районов Рязанской области отклоняется от среднего размера на 11 единиц.
Значение коэффициента вариации свидетельствует о том, что рассмотренная совокупность количественно неоднородная, так как Vs>33%.
Похожие работы
... технологических цепочек; применения общестатистических методов (корреляции, индексного, табличного, графического и др.) к новому объекту исследования — ФПГ. 2. Методика статистического анализа функционирования финансово-промышленной группы и ее технологических цепочек, включающая, разработанные на основе аддитивных, мультипликативных и смешанных моделей, алгоритмы статистического анализа ...
... увеличилась на 2,7%., рентабельность реализованной продукции сократилась на 3,1% Таким образом, предприятие достаточно обеспечено основными ресурсами и эффективность их использования высокая. 3 Экономико-статистический анализ эффективности использования трудовых ресурсов в ОАО «Ново-Вятка» 3.1 Анализ динамики численности работников Одной из важнейших задач статистики является ...
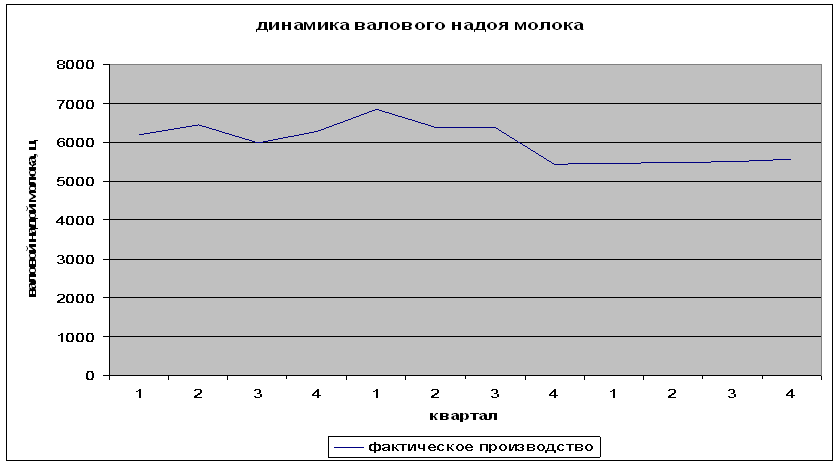
... в 2005году и высокая рентабельность продукции – 42,44% и продаж – 29,79%. В 2006 году отмечается спад прибыли от продаж продукции, а также снижение рентабельности продукции и продаж. 3.Экономико-статистический анализ производства продукции В решении задач, поставленных перед животноводством, большая роль принадлежит статистике. Статистика животноводства прежде всего должна правдиво, глубоко и ...
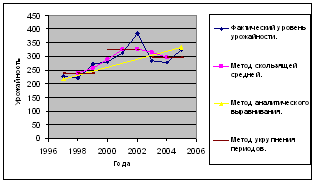
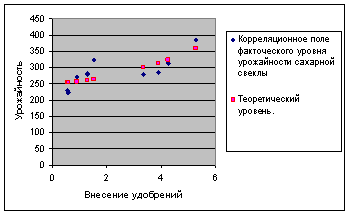
... 0,9 -0,3 Фондоемкость, руб. 0,8 1,0 1,1 +0,3 Производительность труда, тыс. руб. 303,0 310,0 359,7 +56,7 Уровень рентабельности, % +5,7 +7,8 +10 +4,3 3. Экономико-статистический анализ производства сахарной свеклы Экономико-статистический анализ заключается во всестороннем изучении состояния сельского хозяйства, с тем, чтобы сделать выводы о закономерностях его развития и ...
0 комментариев