Навигация
Частотные свойства структурных схем
3. Частотные свойства структурных схем
Площади усиления и статический коэффициент передачи ОУ, входящих в состав D-элементов, не только изменяют коэффициенты передаточной функции, но и повышают ее порядок, что изменяет положение нулей и полюсов и, следовательно, изменяет ожидаемые характеристики и параметры проектируемого устройства. Для учета этого эффекта можно воспользоваться соотношением (7). Тогда, если
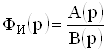 ,
, 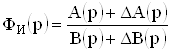 , (19)
, (19)
несложно получить
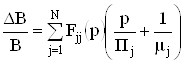 , (20)
, (20)
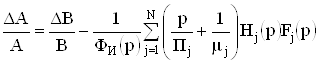 . (21)
. (21)
Полученные соотношения показывают, что уменьшение указанного выше влияния возможно двумя основными способами. В первом случае необходимо увеличивать частоту единичного усиления и коэффициент передачи всех активных элементов. Этот способ является традиционным и связан с ужесточением технологических норм изготовления полупроводниковых компонентов интерфейсных схем. В рамках второго способа решения задачи синтезируются структуры с минимальными вещественными и мнимыми составляющими локальных функций ![]() и произведений
и произведений ![]() . Схемы, обладающие такими свойствами, в соответствии с [6], уместно назвать схемами с собственной компенсацией влияния технологических погрешностей изготовления активных элементов. При этом, как это следует из приведенных соотношений, возможны два основных случая. Во-первых, для различных ОУ локальные передаточные функции
. Схемы, обладающие такими свойствами, в соответствии с [6], уместно назвать схемами с собственной компенсацией влияния технологических погрешностей изготовления активных элементов. При этом, как это следует из приведенных соотношений, возможны два основных случая. Во-первых, для различных ОУ локальные передаточные функции ![]() могут характеризоваться различными знаками, имеющими суммарное (взаимное) влияние на знаменатель передаточной функции. Аналогичный вывод характерен и для числителя, однако здесь необходимо дополнительно рассматривать произведение локальных передаточных функций
могут характеризоваться различными знаками, имеющими суммарное (взаимное) влияние на знаменатель передаточной функции. Аналогичный вывод характерен и для числителя, однако здесь необходимо дополнительно рассматривать произведение локальных передаточных функций ![]() и
и ![]() . Следовательно, целенаправленному изменению могут подвергаться как функция
. Следовательно, целенаправленному изменению могут подвергаться как функция ![]() , так и
, так и ![]() . Во-вторых, аналогичный эффект достигается минимизацией всех указанных локальных передач в рабочем диапазоне частот. В этом случае согласования численных значений Pj и m j не требуется.
. Во-вторых, аналогичный эффект достигается минимизацией всех указанных локальных передач в рабочем диапазоне частот. В этом случае согласования численных значений Pj и m j не требуется.
При микроэлектронной реализации, в частности на БМК, частота единичного усиления и статический коэффициент передачи ОУ оказываются практически идентичными, поэтому при решении целого класса практических задач можно совмещать как собственную, так и взаимную компенсации влияния этих технологических погрешностей на результирующие характеристики проектируемого устройства.
Из соотношения (14) следует, что локальные передаточные функции ![]() , характеризующие влияние ОУ на знаменатель передаточной функции, являются диагональными элементами матрицы (15). В силу того, что базовые D-элементы содержат два ОУ [3], поставленная задача связана с формированием ведущих миноров матрицы второго порядка
, характеризующие влияние ОУ на знаменатель передаточной функции, являются диагональными элементами матрицы (15). В силу того, что базовые D-элементы содержат два ОУ [3], поставленная задача связана с формированием ведущих миноров матрицы второго порядка
![]() (22)
(22)
и может решаться простым перебором альтернативных вариантов соединения активных и пассивных элементов.
Аналогичные условия могут быть сформулированы и для матриц (16) и (17), компоненты которых определяют локальные передаточные функции ![]() и
и ![]() .
.
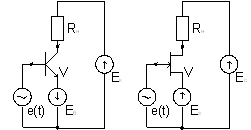
С отмеченных позиций рассмотрим частотные свойства устойчивых D-элементов [3], принципиальные схемы которых в режиме звена второго порядка приведены на рис. 5–6.
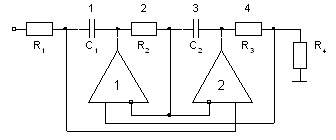
Рис. 5. Звено Антонио с резистивной нагрузкой
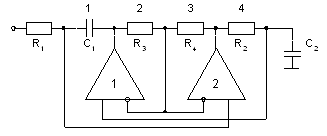
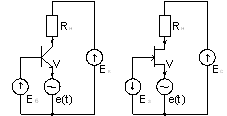
Рис. 6. Звено Антонио с емкостной нагрузкой
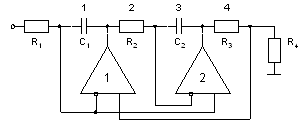
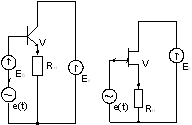
Рис. 7. Звено Брутона с резистивной нагрузкой
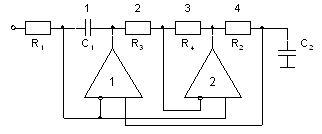
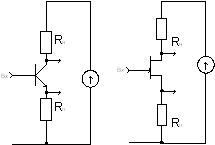
Рис. 8. Звено Брутона с емкостной нагрузкой
Учитывая, что для всех схем ![]() ,
, ![]() , в соответствии с таблицей 1, матрицы частотозависимых цепей будут иметь следующий вид
, в соответствии с таблицей 1, матрицы частотозависимых цепей будут иметь следующий вид
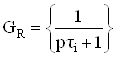 ;
; 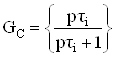 ;
; ![]() , (23)
, (23)
поэтому
![]() . (24)
. (24)
Результаты анализа в соответствии с приведенными соотношениями (табл. 1), (14), (15) сведены в табл. 2 и 3. Как видно из анализа числителей локальных передаточных функций ![]() и
и ![]() , характер влияния площадей усиления входящих в схемы ОУ различен, что и требует более детального сопоставительного анализа схем именно по этому критерию.
, характер влияния площадей усиления входящих в схемы ОУ различен, что и требует более детального сопоставительного анализа схем именно по этому критерию.
Таблица 2
Структура матриц D-элемента
| Схема рис. | Матрицы схем | |||||
|
|
|
|
|
|
| |
| 5 |
|
|
|
|
|
|
| 6 |
|
|
|
|
|
|
| 7 |
|
|
|
|
|
|
| 8 |
|
|
|
|
|
|
| Примечание. Для всех схем | ||||||
Таблица 3
Локальные передаточные функции D-элементов
| Схема рис. | Числитель локальной передаточной функции | |
|
|
| |
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| Примечание. Для всех схем знаменатель передаточной функции имеет вид: | ||
Из (19) и (20) следует, что в общем случае знаменатель передаточной функции будет иметь следующий вид
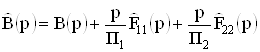 . (25)
. (25)
Как видно из табл. 3,
![]() ,
(26)
,
(26)
![]() . (27)
. (27)
В соответствии с методикой [4] представим полином (25) в окрестности частоты полюса (![]() ) в виде
) в виде
![]() ,
(28)
,
(28)
где
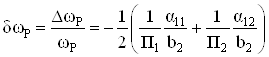 , (29)
, (29)
 . (30)
. (30)
Таким образом, при реализации полного полинома второго порядка в числителе локальных функций ![]() возможна собственная компенсация влияния частоты единичного усиления на затухание полюса; что касается аналогичного влияния на частоту полюса, то это возможно, только когда
возможна собственная компенсация влияния частоты единичного усиления на затухание полюса; что касается аналогичного влияния на частоту полюса, то это возможно, только когда ![]() воспроизводит функцию заграждающего фильтра. Результаты указанных преобразований при
воспроизводит функцию заграждающего фильтра. Результаты указанных преобразований при ![]() для рассматриваемых схем приведены в табл. 4.
для рассматриваемых схем приведены в табл. 4.
Таблица 4
Погрешности реализации параметров полюса
| Схема рис. | Влияние частотных свойств ОУ на параметры звеньев | |
| 5 |
|
|
|
|
| |
| 6 |
|
|
|
|
| |
| 7 |
|
|
|
|
| |
| 8 |
|
|
|
|
| |
Полученные результаты показывают, что потенциально более высокими частотными свойствами характеризуются звенья Антонио. Так, в случае применения идеальных ОУ в схеме рис. 5 при ![]() наблюдается взаимная компенсация влияния первого и второго ОУ на затухание полюса, а в схеме рис. 6 – собственная компенсация, которая свободна от указанного ограничения. Однако ни одна из существующих схем не обеспечивает минимизацию влияния ОУ на положение частоты полюса.
наблюдается взаимная компенсация влияния первого и второго ОУ на затухание полюса, а в схеме рис. 6 – собственная компенсация, которая свободна от указанного ограничения. Однако ни одна из существующих схем не обеспечивает минимизацию влияния ОУ на положение частоты полюса.
Похожие работы
... точности S должен решаться с учетом реализуемого шага и закона перестройки. 5. Влияние неидеальности электронных ключей на свойства базисных структур При построении ЦУП в качестве коммутаторов чаще всего используются МДП ключи (рис. 19, 20). Рис. 19. Принципиальная (а) и эквивалентная (б) схемы i-й ветви ЦУП Рис. 20. Принципиальная (а) и эквивалентная (б) схемы i-й ветви ЦУП ...
... Сравнительная характеристика различных реализаций синтезируемого фильтра. 17 Литература..................................................................................................................................................................... 18 Задание 1. Представить данные на синтез частотно-избирательного фильтра в графической форме с использованием нормированной ...

0 комментариев