Навигация
Вибір критерію оптимальності системи
3 Вибір критерію оптимальності системи
Дуже важливим при розв'язанні задач оптимізації є питання вибору критерію оптимальності системи. Саме критерій оптимальності визначає істинну цінність проектованої системи. Ніякі зручності математичного чи іншого характеру не можуть компенсувати шкідливих наслідків застосування неадекватного критерію оптимальності системи.
Вибір критерію оптимальності, як уже зазначалося, зв'язаний з формалізацією уяви замовника системи про її оптимальність. Існує два підходи до опису переваги одного варіанта системи над іншим: ординалістичний і кардиналістичний.
Кардиналістичний підхід до опису переваги замовника приписує кожній системі ![]() якесь числове значення функції корисності
якесь числове значення функції корисності ![]() . Функція корисності визначає відповідний порядок (або перевагу)
. Функція корисності визначає відповідний порядок (або перевагу) ![]() на множині
на множині ![]() тоді і тільки тоді, коли для різних варіантів
тоді і тільки тоді, коли для різних варіантів ![]() виконуєтся нерівність
виконуєтся нерівність ![]() . У цьому випадку кажуть, що функція корисності
. У цьому випадку кажуть, що функція корисності ![]() є індикатором переваги
є індикатором переваги ![]() . Фактично цей підхід зв'язаний із заданням такої скалярної цільової функції, оптимізація якої у загальному випадку може привести до вибору єдиного найкращого варіанту системи.
. Фактично цей підхід зв'язаний із заданням такої скалярної цільової функції, оптимізація якої у загальному випадку може привести до вибору єдиного найкращого варіанту системи.
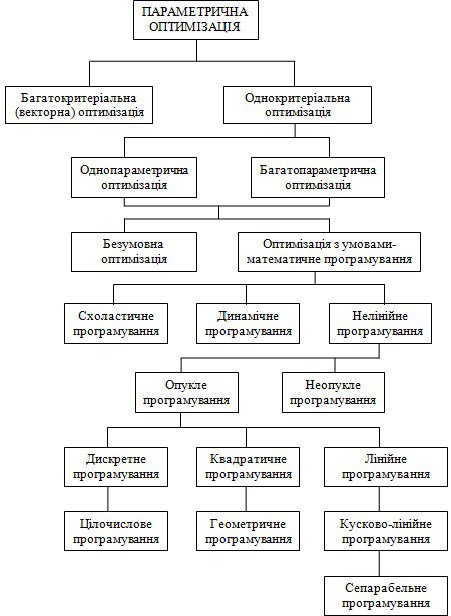
Однак на початкових етапах проектуваннях систем задати скалярну функцію корисності досить складно, тому спочатку вводять сукупність показників якості та зв’язаних з ними цільових функцій (1). Це пов'язано з такими причинами: багатогранність технічних вимог, які висуваються до проектуємої системи; необхідність забезпечення оптимальності системи за різних умов її роботи; система складається з декількох взаємозалежних між собою підсистем і оптимальність системи в цілому визначається ефективністю її складових частин.
У зв’язку з тим, що систему ![]() доводиться характеризувати сукупністю показників якості (цільових функції), це ускладнює процес вибору оптимальних варіантів систем. При цьому мають місце три випадки: показники якості не пов'язані між собою; показники якості зв'язані між собою, але є узгодженими; показники якості зв'язані між собою і є конкуруючими (антагоністичними).
доводиться характеризувати сукупністю показників якості (цільових функції), це ускладнює процес вибору оптимальних варіантів систем. При цьому мають місце три випадки: показники якості не пов'язані між собою; показники якості зв'язані між собою, але є узгодженими; показники якості зв'язані між собою і є конкуруючими (антагоністичними).
У першому випадку знаходження оптимальних варіантів системи виконується шляхом оптимізації по кожній із цільових функцій незалежно
![]() . (2)
. (2)
У другому випадку оптимальні варіанти можуть знаходитися також шляхом оптимізації окремих цільових функцій, тобто цей випадок близький до першого.
У третьому випадку оптимуми по різним цільових функціях не збігаються. Розв’язанням цієї задачі є узгоджений оптимум цільових функцій. Узгоджений оптимум полягає в тому, що досягається мінімальне (максимальне) значення кожнієї цільової функції за умови, що інші цільові функції приймають фіксовані, але довільні значення.
Ординалістичний підхід апелює до порядку (краще-гірше) і базується на введенні певних бінарних відношень на множині допустимих систем. У цьому випадку поняття переваги замовника системи - це бінарне відношення ![]() на множині допустимих систем
на множині допустимих систем ![]() , яке відображує уяву замовника системи, що система
, яке відображує уяву замовника системи, що система ![]() краща за систему
краща за систему ![]() :
: ![]() .
.
На практиці часто при виборі системи на множині ![]() можна керуватися відношенням строгої переваги
можна керуватися відношенням строгої переваги ![]() , що є асиметричним і транзитивним. При цьому система
, що є асиметричним і транзитивним. При цьому система ![]() називається оптимальною за відношенням
називається оптимальною за відношенням ![]() , якщо не існує іншої системи
, якщо не існує іншої системи ![]() , для якої справедливе відношення
, для якої справедливе відношення ![]() . Множина оптимальних систем за відношенням
. Множина оптимальних систем за відношенням ![]() означається як
означається як ![]() . Залежно від структури допустимої множини
. Залежно від структури допустимої множини ![]() і властивостей відношення
і властивостей відношення ![]() множина оптимальних систем може включати єдиний елемент, скінченне або нескінченне число елементів. Якщо відношення нероздільності збігається з відношенням рівності
множина оптимальних систем може включати єдиний елемент, скінченне або нескінченне число елементів. Якщо відношення нероздільності збігається з відношенням рівності ![]() , то множина
, то множина ![]() (якщо вона не порожня) складається з єдиного елемента.
(якщо вона не порожня) складається з єдиного елемента.
Із введенням сукупності цільових функцій кожна система відображується на простір векторних оцінок (критеріальний простір). При цьому вказане відношення строгої переваги існує і для оцінок. Узгодженість відношення переваги на множині проектних рішень ![]() і просторі векторних оцінок
і просторі векторних оцінок ![]() встановлює аксіома Парето. Згідно з нею для будь-яких двох векторних оцінок
встановлює аксіома Парето. Згідно з нею для будь-яких двох векторних оцінок ![]() , що задовольняють векторну нерівність
, що задовольняють векторну нерівність ![]() , завжди виконується відношення
, завжди виконується відношення ![]() .
.
Множину оптимальних оцінок відносно ![]() на просторі
на просторі ![]() називають множиною Парето-оптимальних (оптимальних за Парето) або ефективних оцінок і позначають
називають множиною Парето-оптимальних (оптимальних за Парето) або ефективних оцінок і позначають ![]() . Включення
. Включення ![]() має місце тоді і тільки тоді, коли немає оцінок, для яких виконується нерівність
має місце тоді і тільки тоді, коли немає оцінок, для яких виконується нерівність ![]() . Такий критерій вибору оптимальних рішень називають безумовним критерієм переваги (БКП) або критерієм Парето.
. Такий критерій вибору оптимальних рішень називають безумовним критерієм переваги (БКП) або критерієм Парето.
Проектні рішення, тобто варіанти побудови системи ![]() , для яких справджується включення
, для яких справджується включення ![]() називають Парето-оптимальними відносно векторної цільової функції
називають Парето-оптимальними відносно векторної цільової функції ![]() на множині
на множині ![]() і позначають як
і позначають як ![]() . Іншими словами,
. Іншими словами, ![]() тоді і тільки тоді, коли не існує такої системи
тоді і тільки тоді, коли не існує такої системи ![]() , для якої виконується векторна нерівність.
, для якої виконується векторна нерівність.
![]() . (3)
. (3)
Співвідношення (3) означає, що виконуються нерівності ![]() для всіх
для всіх ![]() і принаймні для одного з показників якості виконується строга нерівність.
і принаймні для одного з показників якості виконується строга нерівність.
Слід зазначити, що відношення строгої переваги ![]() , яке має місце для векторних оцінок, перетворюється при
, яке має місце для векторних оцінок, перетворюється при ![]() на відношення
на відношення ![]() для скалярних оцінок. При цьому Парето-оптимальна оцінка збігається з максимальним елементом множини
для скалярних оцінок. При цьому Парето-оптимальна оцінка збігається з максимальним елементом множини ![]() , якому відповідає оптимум скалярної цільової функції
, якому відповідає оптимум скалярної цільової функції ![]() . Таким чином, поняття Парето-оптимальності слід розглядати як узагальнення поняття оптимуму на випадок кількох цільових функцій. При цьому оптимум за Парето - це узгоджений оптимум зв'язаних між собою і конкуруючих показників якості системи.
. Таким чином, поняття Парето-оптимальності слід розглядати як узагальнення поняття оптимуму на випадок кількох цільових функцій. При цьому оптимум за Парето - це узгоджений оптимум зв'язаних між собою і конкуруючих показників якості системи.
Для Парето-оптимальних проектних рішень характерні такі властивості:
1. Усі елементи множини допустимих варіантів системи ![]() , що не належать до множини Парето-оптимальних
, що не належать до множини Парето-оптимальних ![]() , є безумовно гіршими.
, є безумовно гіршими.
Жодна Парето-оптимальна система з множини ![]() не може бути визнана безумовно гіршою або кращою порівняно з іншою системою цієї множини. Це означає, що всі вони є незрівнянними за критерієм Парето - безумовним критерієм переваги.
не може бути визнана безумовно гіршою або кращою порівняно з іншою системою цієї множини. Це означає, що всі вони є незрівнянними за критерієм Парето - безумовним критерієм переваги.
3. Якщо множина ![]() узгоджена, тобто містить лише один елемент (систему), то відповідний варіант системи є найкращим.
узгоджена, тобто містить лише один елемент (систему), то відповідний варіант системи є найкращим.
4. Кожній Парето-оптимальній системі відповідає потенціально можливе значення кожного із показників якості ![]() , що може бути досягнуто за фіксованих, але довільних значень інших
, що може бути досягнуто за фіксованих, але довільних значень інших ![]() показників якості. Це властивість
показників якості. Це властивість ![]() -кратного оптимуму. Сукупність таких оптимальних значень показників якості є багатовимірними потенціальними характеристиками системи (БПХ).
-кратного оптимуму. Сукупність таких оптимальних значень показників якості є багатовимірними потенціальними характеристиками системи (БПХ).
Похожие работы
... . Таким чином, вивчення особливостей поведінки чотирикомпонентних сумішей полімерів є важливим і тема роботи актуальна. Метою дипломного проекту є створення програмного забезпечення для оптимізації складу чотирикомпонентних нанонаповнених сумішей полімерів, яке дозволить визначати полімерні композиції для отримання виробів з покращеними властивостями. Для досягнення поставленої мети потрібно вирі ...
... ічно зростають показники ефективноств їх діяльності. Науково-дослідні інститути закордоном працюють над новими моделями, які раніше чи пізніше пристосуються до практики управління. Щоб якимось чином впорядкувати та зробити більш наочним питання про сфери застосування тих чи інших моделей і методів наведемо таблицю (див. табл.7).Таблиця 7: Сфери застосування моделей і методів обгруниування управлі ...
... ємозв'язків характеристик, що містяться в ній, з метою отримання прогнозних моделей. Методи аналогій направлені на те, щоб виявляти схожість в закономірностях розвитку різних процесів і на цій підставі проводити прогнози. Випереджаючі методи прогнозування будуються на певних принципах спеціальної обробки науково-технічної інформації, що реалізовують в прогнозі її властивість випереджати розвиток ...
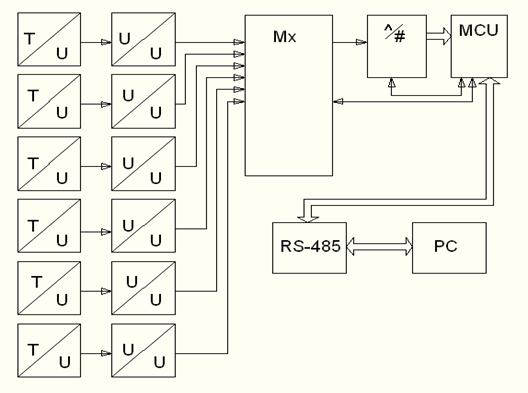
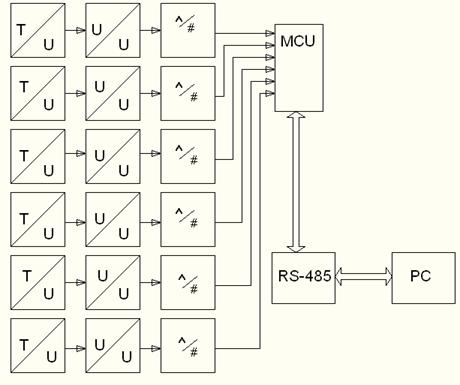
... Розробка структурної схеми системи вимірювання температури 2.1 Вибір оптимального варіанту структурної схеми В даному пункті курсової роботи розробляється структурна схема інформаційно-вимірювальної системи вимірювання температури. Буде розглянуто три варіанта структурних схем, порівняно їх між собою за шістьма критеріями, коротко охарактеризовано кожну та обрано оптимальну структурну схему ...
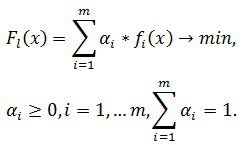



0 комментариев