2.3 Ризик як міра мінливості результату
У якості величини ризику в абсолютному вираженні часто використовується міра розсіювання значень економічного показника відносно центра групування цих значень.
Нехай в якості центра групування значень економічного показника використовується його математичне сподівання. Тоді середньозважене модуля відхилення цього показника від свого математичного сподіваного у дискретному випадку можна знайти за формулою [5.93]:

.
Якщо ж в якості центра групування значень економічного показника використати моду, то середньозважене відхилення від модального значення у дискретному випадку знаходять за формулою:
 .
.
У ситуації, коли адекватною моделлю економічного показника є неперервна випадкова величина
М(|X – M(X)|) = 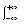 |X – M(X)| f(x)dx,
|X – M(X)| f(x)dx,
М(|X – Mo(X)|) =
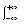
|X – Mo(X)| f(x)dx,
де f(x) — функція щільності розподілу ймовірності.
Очевидно, що більші значення приведених оцінок свідчать про більшу нестабільність щодо діяльності відповідного економічного об’єкта. В якості величини ризику і використовується ця міра нестабільності, тобто:
W = M(|X – M(X)|),
або ж
W = M(|X – Mo(X)|).
Слід мати на увазі, що даний підхід до оцінки ризику застосовується у випадку, коли економічний показник може мати як позитивний, так і негативний інгредієнт (тобто Х = Х±).
При абсолютному вираженні міри ризику під час прийняття економічних рішень широко використовується дисперсійний підхід.
Дисперсією (варіацією) V(X) випадкової величини Х є зважена щодо ймовірності величина квадратів відхилення випадкової величини Х від її математичного сподівання М(Х). Дисперсія характеризує міру розсіяння випадкової величини Х навколо М(Х) і обчислюється за формулою:
V(X) = M(X – M(X))2 = M(X2) – (M(X))2.
Для дискретної випадкової величини
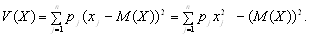
Середньоквадратичним (стандартним) відхиленням випадкової величини Х називається величина
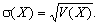
Підхід до оцінки ризику, що спирається на варіацію чи середньоквадратичне відхилення, вважається класичним. Причому чим більшими будуть ці величини, тим більшим буде ступінь ризику, пов’язаного з певною стратегією, тобто величина ризику
W = V(X) або W = s (X).
Слід зазначити, що такий підхід до оцінки ступеня ризику використовується, коли Х = Х±.
Слід мати на увазі, що при класичному визначенні міри ризику однаково трактуються як додатні, так і від’ємні відхилення величини реального ефекту від сподіваної величини, тобто виконується гіпотеза про те, що коливання випадкової величини Х (прибутку, ЧПВ, збитків) в обидві сторони однаково небажані. Але у ряді випадків це не так і цю гіпотезу доводиться відкидати.[4.67]
Якщо випадкова величина Х = {x1; …; xn} відображає прибутки (Х = Х+) і значення хi < M(X) (оцінка прибутку хі є реалізацією випадкової величини Х і є меншою від сподіваної величини прибутку), то це є ознакою несприятливої ситуації. В той же час додатне відхилення вказує на те, що реалізація випадкової величини (прибутку) є більшою, ніж сподівана величина, і це для менеджера (інвестора) є, очевидно, кращою, тобто сприятливою ситуацією.
У неокласичній теорії економічного ризику виходять з того, що ризик пов’язаний лише з несприятливими для менеджера (інвестора) ефектами і для його оцінювання достатньо брати до уваги лише несприятливі відхилення від сподіваної величини. [2.231] При цьому в якості міри ризику використовується семі варіація, яка обчислюється за формулою:

де  aj — індикатор несприятливих відхилень, який визначають за формулою:
aj — індикатор несприятливих відхилень, який визначають за формулою:

Якщо ж, наприклад, Х = {x1; …; xn} відображає можливі варіанти збитків (Х = Х –, тобто має негативний інгредієнт), то
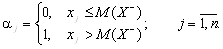
Для неперервної випадкової величини Х відповідно:
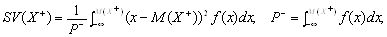
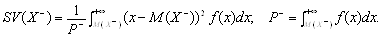
З практичної точки зору зручніше (беручи до уваги вимірність величин) застосовувати семі квадратичне відхилення.
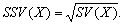
Згідно із сказаним вище чим більшою буде величина SV(X) (чи SSV(X)), тим більшим буде ступінь ризику,
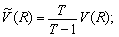
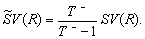
Для оцінки ризику можна використовувати також середньоквадратичне відхилення від зваженого середньо геометричного:

,
або ж оцінку цієї величини на основі статистичних даних:

.
Виявляється, що портфель цінних паперів, сформований на підставі максимізації зваженої середньо геометричної норми прибутку, характеризується найвищою очікуваною вартістю в кінці середньо - та довготермінового періоду (найвищим кінцевим багатством).
З точки зору неокласичного підходу до оцінки ризику доцільним є впровадження такого показника ступеня ризику, як семі квадратичне відхилення від зваженого середньо геометричного випадкової величини [11.156]:

,
де SG(X) — величина семі варіації по відношенню до зваженого середньо геометричного SSG(X) — семі квадратичне відхилення, aj — індикатор j-го несприятливого відхилення.
Оскільки величина SG(X) має негативний інгредієнт, то, як і раніше, ризик вважається більшим при більших значеннях SG(X) (чи SSG(X)).
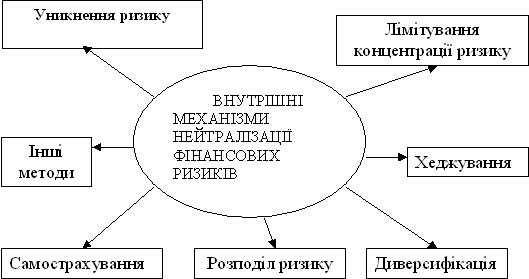
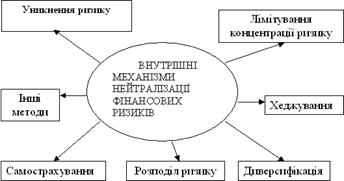
... впливати на об'єкт і примушувати його діяти для досягнення цілей, які поставив перед собою суб'єкт управління. 1.3 Механізми нейтралізації фінансових ризиків В системі методів управління фінансовими ризиками підприємства основна роль належить внутрішнім механізмам їх нейтралізації. Внутрішні механізми нейтралізації фінансових ризиків являють собою систему методів мінімізації їх негативних ...
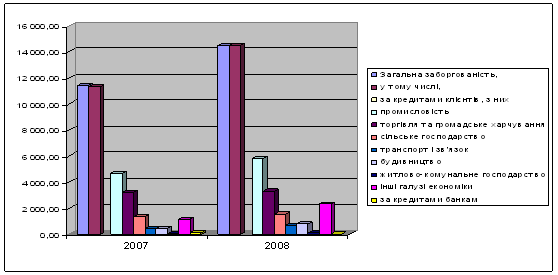
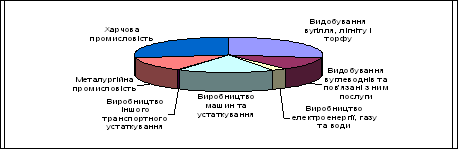
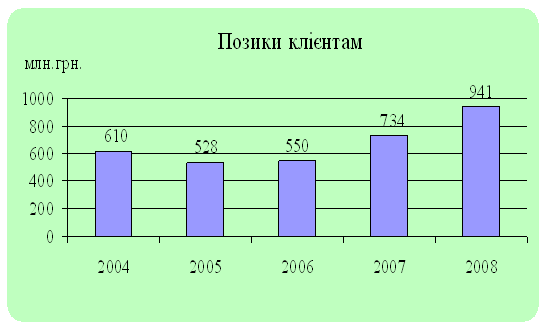
... та методів аналізу процесу банківського кредитування на прикладі комерційного банку Промінвестбанк, який є одним із лідерів кредитування української економіки. Глава 2. Управління кредитними ризиками в діяльності комерційних банків (на прикладі Промінвестбанку) 2.1 Аналіз процесу банківського кредитування в Промінвестбанку Акціонерний комерційний промислово-інвестиційний банк «Промі ...
... портфеля банку: - диверсифікація; - лімітування; - створення резервів для відшкодування втрат за кредитними операціями комерційних банків. Класифікацію методів управління кредитним ризиком наведено в схемі 2.1. (додаток Т). Методи управління ризиком кредитного портфеля банку, які застосовуються в АКБ “Укрсоцбанк”: Диверсифікація. Метод диверсифікації полягає у розподілі кредитного ...
... фінансових ризиків; диверсифікація фінансових ризиків; хеджування фінансових ризиків на основі похідних цінних паперів. Для досліджуємого міжнародного ринку золота основним методом нейтралізації ризиків угод є хеджування фінансових ризиків на основі похідних цінних паперів золотого ринку – стандартних ф’ючерсно-опціонних угод. У застосуванні до сегменту фінансового ринку золота, кількісні ...
![]() .
.![]() |X – M(X)| f(x)dx,
|X – M(X)| f(x)dx,![]()
![]()
![]()
![]() aj — індикатор несприятливих відхилень, який визначають за формулою:
aj — індикатор несприятливих відхилень, який визначають за формулою:![]()
![]()

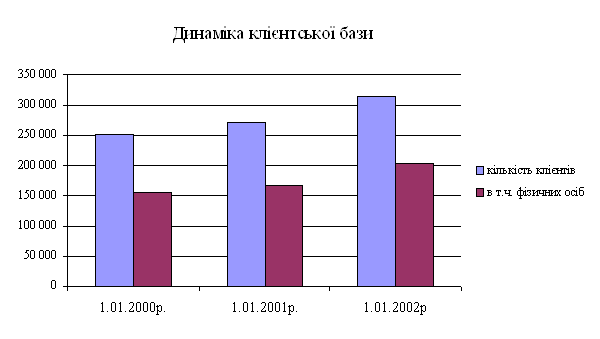


0 комментариев