Расчет аналитических и средних показателей динамики

1. Расчет аналитических и средних показателей динамики

Ряд динамики (динамический ряд, временной ряд) представляет собой ряд расположенных в хронологической последовательности статистических величин, которые отражают развитие изучаемых явлений. Каждый ряд динамики имеет два основных элемента:

время (t);

уровень ряда (yi), т.е. конкретные значения показателя.

Уровни динамического ряда могут быть выражены абсолютными, средними и относительными величинами.

При изучении динамики явлений для характеристики особенности их развития на отдельных этапах рассчитывают производные показатели: абсолютный прирост, коэффициент роста, темп роста и прироста, абсолютное значение 1% прироста. Расчет основан на сравнении уровней ряда динамики.

В зависимости от базы сравнения различают базисные и цепные показатели динамики. Базисные показатели динамики — это результат сравнения текущих уровней с одним фиксированным уровнем, принятым за базу. Они характеризуют окончательный результат всех изменений в уровнях ряда за период от базисного до текущего уровня. Обычно за базу сравнения принимают начальный уровень динамического ряда. Цепные показатели динамики — это результат сравнения текущих уровней с непосредственно предшествующими. Они характеризуют интенсивность изменения уровней от срока к сроку.

Абсолютный прирост равен разности между текущим уровнем и уровнем более раннего периода. Интерпретацию абсолютного прироста осуществляют в тех же единицах измерения, в которых измеряют уровни ряда, с добавлением единицы времени, за которую определено изменение. Если текущий уровень уменьшился по сравнению с предыдущим периодом, то абсолютный прирост, имея отрицательное значение, характеризует абсолютную убыль (сокращение) уровня. Абсолютный прирост за единицу времени отражает абсолютную скорость изменения. Формулы абсолютного изменения уровня динамического ряда следующие:

цепного Dуц = уi - уi-1 ;

базисного Dуб = уi - у0,

где Dу — абсолютный прирост за t единиц времени; уi — текущий (сравниваемый) уровень ряда; уi-1 — уровень ряда, непосредственно предшествующий текущему; уо — уровень ряда, который принят за базу сравнения.

Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных приростов равна соответствующему базисному приросту за весь период.

Для оценки эффективности изменения уровня динамического ряда используют относительные показатели динамики:

коэффициент роста, выраженный в долях единицы;

темп роста, выраженный в %.

Коэффициент роста Кр определяют по формулам:

• цепной ;

• базисный .

Взаимосвязь цепных и базисных коэффициентов роста заключается в следующем:

а) произведение цепных коэффициентов роста равно базисному коэффициенту роста за весь период.

б) частное от деления последующего базисного коэффициента роста на предыдущий равна соответствующему цепному коэффициенту роста.

Для большей простоты и наглядности доказательства этой взаимосвязи используем данные за три периода:

а)

б)

Коэффициент роста показывает, во сколько раз увеличился уровень динамического ряда по сравнению с базисным, а в случае уменьшения — какую часть базисного составляет сравниваемый уровень. Темпы и коэффициенты роста отличаются только единицами измерения. Формулы расчета темпов роста следующие:

• цепного ;

• базисного .

Темпы прироста (сокращения) так же, как и темпы роста, исчисляют по годам (цепным методом) и накопленным итогом за длительный период (базисным методом). Формулы расчета темпов прироста следующие:

Цепного

Базисного

Темп прироста показывает, на сколько процентов изменилась величина уровня динамического ряда за изучаемый период времени. Если она сокращается, то темпы прироста будут иметь знак "минус" и характеризовать относительное уменьшение уровней ряда.

Для правильной интерпретации относительных показателей динамики явлений рекомендуется рассматривать их совместно с исходными уровнями ряда.

Если уровень ряда принимает положительные и отрицательные значения (например, финансовый результат деятельности организации может быть прибылью или убытком), то темпы изменения и прироста не имеют экономической интерпретации и не рассчитываются.

Для цепных показателей прироста и его темпов рассчитывают показатель абсолютного значения одного процента прироста. Он равен отношению абсолютного прироста (цепного) к темпу прироста (цепному). Этот показатель может быть исчислен и иначе, т.е. как одна сотая часть предыдущего уровня:

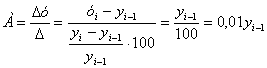
Аналитическое значение данного показателя состоит в том, что при возрастающей скорости (и растущем уровне) темпы роста могут иметь тенденцию к уменьшению или оставаться без изменения. В результате абсолютное значение одного процента прироста будет расти.

Затухающий темп прироста вовсе не означает приостановки роста: при высоких абсолютных уровнях развития изучаемого явления может значительно увеличиться его абсолютный объем даже при небольшой величине темпов. Следовательно, чтобы правильно оценить значение показателя темпа, его нужно рассматривать не изолированно, а совместно с абсолютными показателями уровня и прироста. В статистической практике динамика стоимостных показателей оценивается с учетом уровня инфляции.

Для анализа интенсивности изменения во времени одного явления по сравнению с другим рассчитывают коэффициент опережения (Коп). Он представляет собой отношение базисных темпов роста двух динамических рядов за одинаковые отрезки времени:

где К1,К2 — базисные темпы роста соответственно первого и второго рядов динамики.

Коэффициент опережения показывает, во сколько раз быстрее растет уровень одного ряда динамики по сравнению с уровнем другого. При таком сопоставлении темпы должны характеризовать тенденции одного направления.

Показатели динамики с переменной базой сравнения (цепные) используют для выявления типа изменения уровней ряда. В статистической практике в соответствии с показателями динамики различают следующие типы изменений:

- равномерный рост или снижение (цепные абсолютные приросты одинаковы);

- ускоренный рост или снижение (цепные приросты систематически увеличиваются по абсолютной величине);

- замедленный рост или снижение (цепные приросты систематически уменьшаются тоже по абсолютной величине).

Чтобы получить обобщенную характеристику скорости темпов развития изучаемого явления в пределах рассматриваемого периода, рассчитывают средние показатели динамического ряда за единицу времени.

Средние характеристики ряда динамики

Для обобщающей характеристики динамики используют два типа средних показателей:

средние уровни ряда;

средние показатели изменения уровней ряда.

Для рядов динамики с равноотстающими по времени уровнями порядок расчета среднего уровня следующий:

а) находим средний уровень интервального ряда абсолютных величин:

б) определяем средний уровень моментного ряда абсолютных величин:

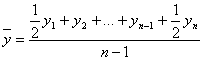
Средний уровень интервального ряда абсолютных величин соответствует рассмотренной выше категории определяющего показателя. Поскольку, как уже отмечалось, уровни такого ряда можно суммировать, то справедливо равенство:

у1+у2+…+уп=

Следовательно,

где п — число уровней ряда.

Средний уровень моментного ряда с равноотстающими уровнями рассчитывается в предположении, что в пределах каждого периода, разделяющего моментные наблюдения, развитие явления происходило по линейному закону. Тогда общий средний уровень вычисляется как среднее значение из средних по каждому интервалу:

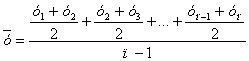
В итоге получаем следующую формулу средней хронологической:

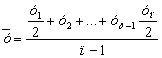
Для моментного ряда с неравными промежутками времени при известных точных датах изменения уровней ряда средний уровень определяется по формуле

где t - время, в течение которого сохранялся уровень.

Средние показатели изменения уровней ряда включают:

средний абсолютный прирост();

средний коэффициент роста (р);

средний темп роста ();

средний темп прироста (Р).

Средний абсолютный прирост показывает, на сколько единиц в среднем увеличивался или уменьшался каждый уровень ряда по сравнению с предыдущим за ту или иную единицу времени (в среднем ежемесячно, ежегодно и т.п.).

Средний абсолютный прирост характеризует среднюю абсолютную скорость роста (или снижения) уровня ряда. Его рассчитывают в зависимости от исходных данных следующими способами:

как простую среднюю арифметическую из абсолютных приростов (цепных) за последовательные промежутки времени

где t — продолжительность периода.

как частное от деления базисного абсолютного прироста конечного уровня ряда на продолжительность периода (число усредняемых отрезков времени от базисного до сравниваемого периода):

через накопленный (базисный) абсолютный прирост (Dуб):

Средний коэффициент роста (снижения) показывает, во сколько раз в среднем за единицу времени изменяется уровень ряда динамики. Для его вычисления используют формулу геометрической средней в предположении, что соблюдается равенство фактического отношения конечного уровня к начальному при замене фактических темпов на средние. В зависимости от наличия исходных данных расчет проводят следующим образом:

если исходной информацией служат цепные коэффициенты роста, то формула имеет вид:

где П — произведение цепных показателей динамики.

через базисный коэффициент роста конечного периода ()

если известны уровни динамического ряда,

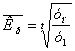
Средний темп роста представляет собой средний коэффициент роста, выраженный в процентах (= *100). Отсюда средний темп прироста D=  - 100.

По данным таблицы рассчитаем абсолютный прирост:

цепной Dуц = уi - уi-1 ;

базисный Dуб = уi - у0,

где Dу — абсолютный прирост за t единиц времени; уi — текущий (сравниваемый) уровень ряда; уi-1 — уровень ряда, непосредственно предшествующий текущему; уо — уровень ряда, который принят за базу сравнения.

2008 год:

II квартал:

III квартал:  844,3-719,8=124,5

IV квартал:  880,0-719,8= 160,2

2009 год:

II квартал: 944,5-894,0= 50,5

III квартал: 989,4-894,0= 95,4

IV квартал: 1012,1-894,0= 118,1

2010 год:

II квартал: 1067,2-1028,8= 38,4

III квартал: 1091,1- 1028,8= 62,3

IV квартал: 1123,2-1028,8= 94,4

Темп роста:

цепной ;

базисный .

2008 год:

II квартал:

III квартал:

IV квартал:

2009 год:

II квартал:

III квартал:

IV квартал:

2010 год:

II квартал:

III квартал:

IV квартал:

 844,3-819,0=25,3

 880,0-844,3= 35,7

 989,4-944,5= 44,9

 1012,1-989,4= 22,7

 1091,1-1067,2= 23,9

 1123,2-1091,1= 32,1

Темп прироста:

цепной:

, где - цепной темп роста;

базисный:

, где - базисный темп роста.

2008 год:

II квартал:  

III квартал:  

IV квартал:  

2009 год:

II квартал:  

III квартал:  

IV квартал:  

2010 год:

II квартал:  

III квартал:  

IV квартал:  

Средний абсолютный прирост:

,

где - накопленный (базисный) абсолютный прирост,

t — продолжительность периода

2008 год:

2009 год:

2010 год:

Средний темп роста

,

где  - базисный коэффициент роста конечного периода,  - базисный коэффициент роста, t – продолжительность периода.

= *100

2008 год:

=

2009 год:

=

2010 год:

=

Средний темп прироста

D=  - 100, где  - средний темп роста

2008 год:

D= 105,15 – 100= 5,15%

2009 год:

D= 103,15 – 100= 3,15%

2010 год:

D= 102,22 – 100= 2,22%

Средний уровень интервального ряда абсолютных величин:

,

где n - число уровней ряда.

2008 год:

2009 год:

2010 год:

Результаты вычислений представлены в таблицах:

Таблица 1.1 Аналитические показатели динамики

Квартал года			,%	,%	,%	,%
II.2008	99,2	99,2	113,78	113,78	13,78	13,78
III.2008	124,5	25,3	117,3	103,09	17,3	3,09
IV.2008	160,2	35,7	122,26	104,23	22,26	4,23
II.2009	50,5	50,5	105,65	105,65	5,65	5,65
III.2009	95,4	44,9	110,67	104,75	10,67	4,75
IV.2009	118,1	22,7	113,21	102,29	13,21	2,29
II.2010	38,4	38,4	103,73	103,73	3,73	3,73
III.2010	62,3	23,9	106,06	102,24	6,06	2,24
IV.2010	94,4	32,1	109,18	102,94	9,18	2,94

Таблица 1.2 Средние показатели динамики

Годы		,%	D,%
2008	40,05	105,15	5,15	815,775
2009	29,525	103,15	3,15	960
2010	23,6	102,22	2,22	1077,575

Проанализировали динамику, тенденции изменения. Заметили, что абсолютный прирост, базисный и цепной, постепенно увеличивается к концу года, что говорит о нарастании объема денежных единиц за реализацию продукции. Также увеличивается темп роста и темп прироста. Средний абсолютный прирост по годам, напротив, уменьшается, так же как и темп роста и темп прироста, что свидетельствует о более плавном нарастании объема денежных средств за реализацию продукции в последующие года.