Навигация
Задача аналізу розімкнутої системи з очікуванням (потоки вимог Пуасоновські)
1.1.2.2 Задача аналізу розімкнутої системи з очікуванням (потоки вимог Пуасоновські)
а) Постановка задачі.
Нехай дана деяка система масового обслуговування, для котрої справедливі наступні гіпотези:
1) ймовірність надходження вимог не залежить від прийнятого початку відліку часу, а залежить тільки від часу періоду спостереження (потік стаціонарний)
2) не надходять до систему і не покидають її одночасно 2 чи більше вимог (потік стаціонарний)
3) надходження однієї вимоги не залежить від надходження іншої (відсутність післядії). Відомі також інтенсивність ![]() надходження потоків вимог (середнє число обслуговування за одиницю часу -
надходження потоків вимог (середнє число обслуговування за одиницю часу - ![]() ). Потрібно визначити основні характеристики системи, а саме:
). Потрібно визначити основні характеристики системи, а саме:
- P – ймовірність простою каналу обслуговування
- ![]() - ймовірність того, що в системі знаходяться n-вимог
- ймовірність того, що в системі знаходяться n-вимог
- ![]() - середнє число вимог, що знаходяться в системі
- середнє число вимог, що знаходяться в системі
- ![]() - середнє число вимог, що знаходяться в черзі
- середнє число вимог, що знаходяться в черзі
- ![]() - середній час очікування вимог в системі.
- середній час очікування вимог в системі.
Потік вимог, що володіє якостями стаціонарності, ординарності та відсутністю післядії, називають простішим. В нашій задачі потік вимог простіший. Основним поняттям при аналізі процесу системи масового обслуговування є стан системи. Знаючи стан системи можна передбачити у ймовірностному сенсі її поведінку. Простіший потік – це стаціонарний Пуасоновський потік. Якщо всі потоки подій, що переводять систему із одного стану до іншого являються Пуасоновськими, то для цих системи ймовірність стану описується за допомогою систем звичайних диференційних рівнянь. В більшості задач не прикладного характеру заміна неПуасоновського потоку подій Пуасоновським з тими ж інтенсивностями призводить до отримання рішення, котре мало відрізняються від істинного, а іноді і зовсім не відрізняється. В якості критерію відмінності реального стаціонарного потоку від Пуасоновського можна розглядати близькість математичного очікування числа дисперсій подій, що надходять на визначеній ділянці часу в реальному потоці.
Існує визначений математичний прийом, що значно полегшує вивід диференційного рівняння для ймовірностного стану. Спочатку будується розмічений граф стану з показом можливих переходів. Це полегшує дослідження та робить його більш наглядним. Граф стану, на котрому проставлені не тільки стрілки переходів, але й інтенсивність відповідних потоків подій називають розміченим.
Закреслимо розмічений граф стану одноканальної розімкнутої системи масового обслуговування з очікуванням (рисунок 1.3):
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ........
........
![]()
|
|
|
|
|
Рисунок 1.3
Якщо складений розмічений граф стану, то для побудови математичної моделі, тобто для складання системи звичайних диференційних рівнянь рекомендується використовувати наступні правила:
- Похідна ![]() ймовірності перебування системі у стані n дорівнює алгебраїчній сумі наступних величин: число величин цієї суми дорівнює числу стрілок на графі стану системи, що з’єднує стан n з іншими станами.
ймовірності перебування системі у стані n дорівнює алгебраїчній сумі наступних величин: число величин цієї суми дорівнює числу стрілок на графі стану системи, що з’єднує стан n з іншими станами.
- Якщо стрілка направлена в стан n, то відповідна величина береться зі знаком “+” .
- Якщо стрілка направлена зі стану n – то зі знаком “-“.
- Кожна величина суми дорівнює добутку ймовірностей того стану, з котрого направлена стрілка на інтенсивність потоку подій, що переводять систему по даній стрілці.
У відповідності з розміченим графом стану, використовуючи даний стан, запишемо систему звичайних диференційних рівнянь ймовірностей стану таким чином:
![]() ;
;
![]()
б) Дослідження математичної моделі.
Обмежемся дослідженням режиму роботи що встановився замкнутої одноканальної системи. Тоді:
![]() (n=0,1,...)
(n=0,1,...)
Дійсно, замість системи диференційних рівнянь отримуємо систему алгебраїчних рівнянь:
![]()
![]()
![]()
Використовуючи отриману систему алгебраїчних рівнянь легко виразити ймовірності стану системи у вигляді квадратної рекурентної формули . З першого рівняння визначається ймовірність присутності однієї вимоги в системі.
![]()
Із другого рівняння ймовірність присутності двох вимог в системі:
![]()
І в результаті отримуємо:
![]()
Аналогічно проводиться перетворення для ![]()
![]()
![]()
І врешті сумуємо отримані значення ![]() та знаходимо суму:
та знаходимо суму:
![]()
![]()
![]()
Використовуючи формулу геометричної прогресії отримуємо:
![]()
і при ![]()
![]() , сума:
, сума:
![]()
Звідки ми маємо:
1) ймовірність простою каналу обслуговування: ![]()
2) знаходимо ймовірність того, що в системі знаходиться ![]() вимог:
вимог:
![]()
3) середнє число вимог, що знаходяться в системі:
![]()
![]()
Остання дужка є похідною від наступного виразу:
![]()
![]() ,
,
тобто цей вираз дорівнює: ![]()
В результаті отримуємо: ![]()
4) Далі знаходимо середнє число вимог, що знаходяться в черзі:
![]()
5) Знаходимо середній час очікування вимоги в системі, котрий можливо визначити, знаючи середнє число вимог, що знаходяться в системі:
![]()
Похожие работы
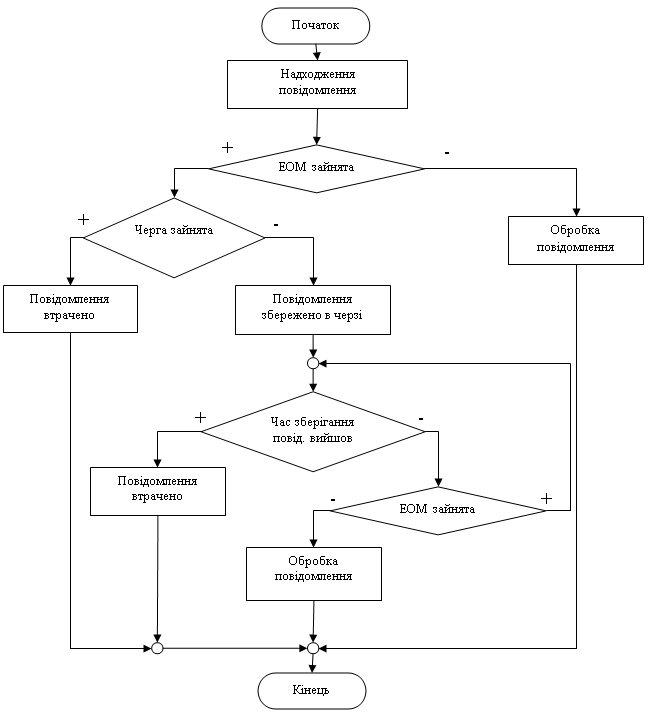
....................................... 23 Додаток Г – результати роботи програми............................................................. 24 Вступ Темою данної курсової роботи є моделювання процесу надходження до ЕОМ повідомлень від датчиків та вимірювальних пристроїв. Це обумовлено тим, що постійне впровадження системи збирання та обробки інформації вимагає збільшення кількост ...
... їх обробки на ЕОМ можна представити у вигляді СМО. Тобто, модель заданої системи є дискретною стохастичною системою. Виконання імітаційного моделювання вказаного процесу надходження повідомлень від датчиків до ЕОМ та їх обробки на ЕОМ потребує проведення моделювання (імітацію) всіх подій, які можуть статись – отримання інформаційних повідомлень від датчиків, вхід і звільнення пам'яті ЕОМ, втрату ...
... кта та алгоритму його функціонування, або алгоритму процесу, а також уявлення опису на різноманітних мовах здійснюється взаємодією людини і ЕОМ. Система автоматизованого проектування - це комплеск засобів автоматизації проектування, взаємозв’язаних з необхідними підрозділами проектної організації або колективом спеціалістів (користувачем системи), які виконують автоматизоване проектування. САПР ...
... модель, яка опосередковує відносини між об’єктом, який вивчається, та суб’єктом, який пізнає (системним аналітиком). Головним гальмом для практичного застосування математичного моделювання в економіці є проблема наповнення розроблених моделей конкретною та якісною інформацією. Точність і повнота первинної інформації, реальні можливості її збору й опрацювання справляють визначальний вплив на виб ...
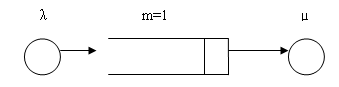




0 комментариев