Навигация
Расчет параметров электрической цепи
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА И ПРОДОВОЛЬСТВИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра электротехники
Расчетно-графическая работа
Тема: «Расчет параметров электрической цепи»
Выполнили: студенты 4 курса
2 эа группы АЭФ
Джунковский В.В., Дацук Е.В.
Проверил: Громова В.С.
Минск – 2010
Задание
Вариант 51
Схема 3.11
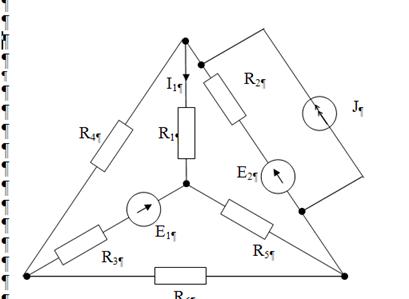
Дано:
E1 =125 B
E2 =34 B
R1 =10 Ом
R2 =40 Ом
R3 =50 Ом
R4 =17.5 Ом
R5 =75 Ом
R6 =20 Ом
J =0.2 А
Требуется:
1. Составить на основе законов Кирхгофа систему уравнений для расчета токов во всех ветвях схемы.
2. Определить токи во всех ветвях схемы методом контурных токов. Расчет системы уравнений выполнить методом определителей.
3. Составить уравнения для расчета токов во всех ветвях схемы методом узловых потенциалов.
4. Составить баланс мощностей, вычислив суммарную мощность источников и суммарную мощность приемников.
5. Определить ток I1 методом эквивалентного генератора.
ток генератор уравнение

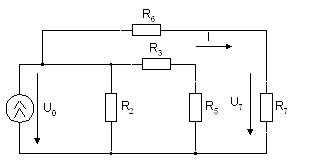
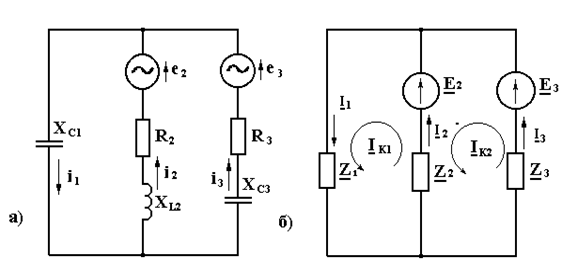
1. Определяем по первому закону Кирхгофа токи в ветвях относительно узлов а, b, с (смотреть рис.2)
Узел а: I2-I4+Iк-I1=0
Узел b: I4 -I3 -I6=0
Узел с: I3+I1-I5=0
Составим уравнения по второму закону Кирхгофа (смотреть рис.2).
контур abcа : I4 R4+I3 R3-I1 R1=E1
контур bcdb : I3 R3+I5 R5- I6 R6=E1
контур acdа : I1 R1+I5 R5+ I2 R2=E2
Из составленных уравнений составим систему и подставим все известные величины
![]() I2-I4+0.2Iк-I1=0
I2-I4+0.2Iк-I1=0
I4 -I3 -I6=0
I3+I1-I5=0
10I1+50I3+17.5I4=125
50I3+75I5-40I2=125
17.5I4-20I6-50I5=34
2. Определим токи во всех ветвях схемы методом контурных токов
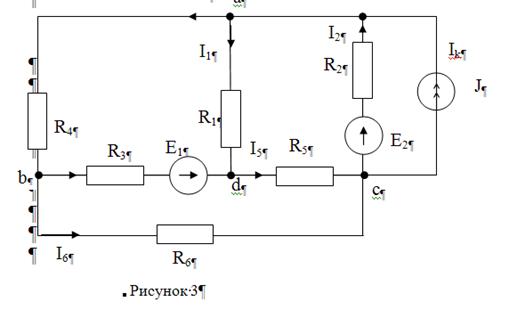
Выберем независимые контуры и придадим им контурные токи. Составим уравнения по второму закону Кирхгофа (смотреть рис.3).
![]() I11(R1+R3+R4) -I22R3-I33R1=E1
I11(R1+R3+R4) -I22R3-I33R1=E1
I22(R6+R5+R3)-I11R3-I33R5 =-E1
I33(R2+R1+R5)-I22R5-I11R1-Iк1R2=E2
77.5I11-50I22-10I33=125
![]() -50I11+145I22-75I33=-125
-50I11+145I22-75I33=-125
-10I11-75I22+125I33=42
Рассчитаем систему методом определителей:
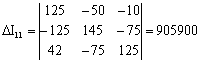
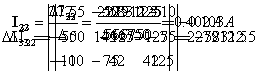
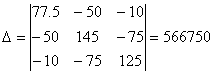
Рассчитываем токи:
I1=I33-I11=-1.196 A
I2=I33-Ik=0.202 A
I3= I11-I22=1.701 A
I4=I11=1.598 A
I5=I33-I22=0.505 A
I6=I22=-0.103 A
Сделаем проверку по второму закону Кирхгофа.
I4 R4+I3 R3-I1 R1=E1
27,965+85,05+ 11,96=125
I3 R3+I5 R5- I6 R6=E1
85,05+37,875+2,06=125
I1 R1+I5 R5+ I2 R2=E2
-11,96+37,875+8,08=34
Похожие работы
... . При расчетах реальные электрические цепи заменяют эквивалентными схемами, в которых реальные устройства заменены совокупностью идеальных (т.е. обладающих одним свойством) элементов, что упрощает расчеты. Задачей теории линейных электрических цепей является изучение совместного действия всех образующих цепь элементов общими методами независимо от физических процессов, определяющих их работу. ...
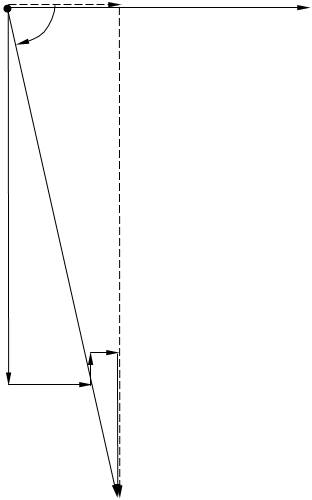
... диаграмма построена на рисунке 4. Ia2 MI= 0,5 А/см МU= 25 В/см I2 I1=Ip1 Ip2 OIa U Ia3 I3 Ip3 Ip I Рисунок 43 Расчёт сложных цепей переменного тока символическим методом Электрическая схема цепи и комплексная схема замещения представлены на рисунке 5а и б соответственно. Рисунок 5 Намечаем в независимых контурах заданной цепи, как показано на рисунке 5б, ...
... Мгновенное напряжение на проводимости G =10 Cм при заданном токе i=12sin(ωt+φ) равно: u=1,2sin(ωt + φ) 4. Электрические цепи при гармоническом воздействии в установившемся режиме Основные свойства линейных цепей: Принципа суперпозиции. Независимыми называют узлы, которые: отличаются одной ветвью. Независимыми называются контура, которые: отличаются одной ...
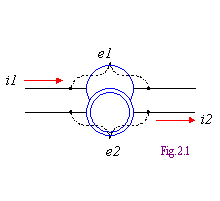
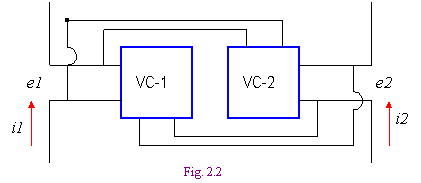
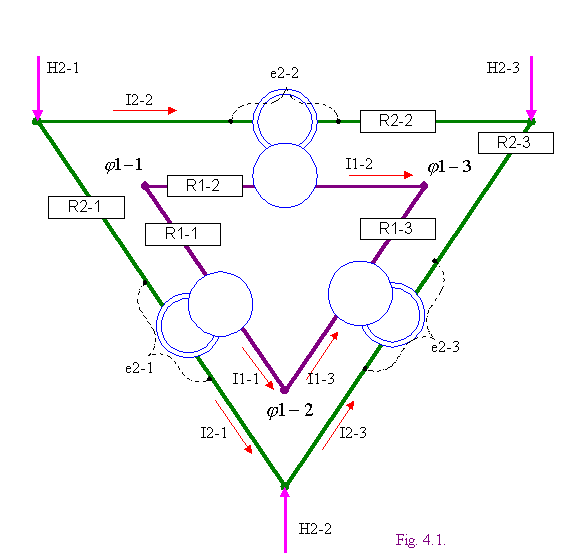
... . Однако, после решения задачи эти фазы становятся известными. 7. Электрическая цепь, как модель оперативной коррекции Рассмотрим сдвоенную электрическую цепь с синусно-косинусными преобразователями СКП, как модель оперативной коррекции в энергосистеме (ср. также с фиг. 4.1 и см. также [3, 6, 7]). Будем использовать в ней для обозначения токов, потенциалов, напряжений и сопротивлений те же ...
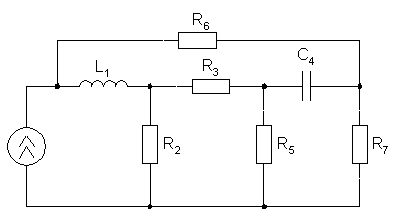
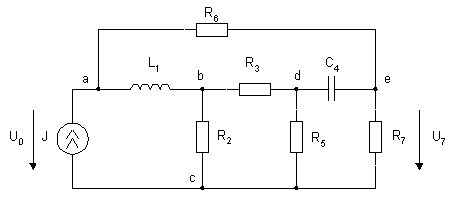


0 комментариев