Функция не периодична

4. Функция не периодична.

5. Находим первую производную . Производная  для всех . Это значит, что функция возрастает на всей числовой оси. Поэтому экстремумов она не имеет.

6. Находим вторую производную 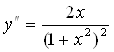 и приравниваем её к нулю: . Точка  будет критической точкой. Точкой  разбиваем область определения функции на интервалы  и , являющиеся интервалами знакопостоянства второй производной.

	—		+
	выпуклая		вогнутая

Поскольку при переходе через точку  производная  меняет знак, то точка  будет точкой перегиба искомой кривой.

7. Выясним наличие наклонных асимптот:

;

;

; .

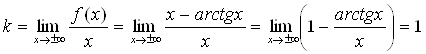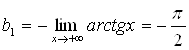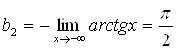Следовательно, наклонными асимптотами будут прямые:

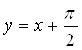 и .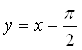

Задача 28

Найти частные производные функции

.

 

Решение

; ; .

 

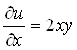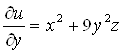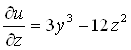Задача 29

Найти производную функции  в точке  в направлении вектора .

 

Решение

 

; ; ; ; ; ; .

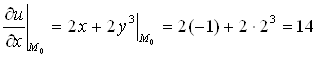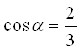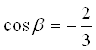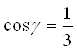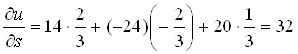Задача 30

Даны функция  и точки  и . Вычислить:

1)  точное значение  функции в точке ;

2)  приближенное значение  функции в точке, исходя из её значения в точке , заменив приращение  при переходе от точки  к точке  дифференциалом ;

3)  относительную погрешность, возникающую при замене  на .

Решение

По условию , , , . Поэтому , . Находим точное значение функции в точке :

.

Находим приближенное значение :

;

; .

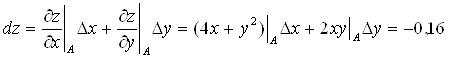Вычисляем относительную погрешность:

.

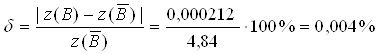Задача 31

Найти экстремумы функции

.

Решение

Находим критические точки:

; ;

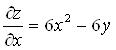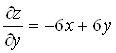откуда  и  - точки, где частные производные равны нулю. Исследуем эти точки с помощью достаточных условий

;

;

;

;

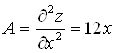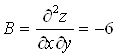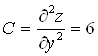. Поэтому экстремума в точке  функция не имеет.

, . Поэтому функция в точке  имеет минимум: .

Задача 32

Вычислить неопределенный интеграл

.

 

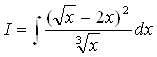Решение

 

Возводим в квадрат числитель и почленно делим на знаменатель. Затем, применяя свойства, получаем первый интеграл таблицы:

.

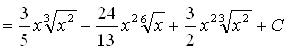Задача 33

Вычислить неопределенный интеграл

.

 

Решение

 

Принимая в подынтегральном выражении , , получим , . Поэтому

.

Проверка. .

 

Задача 34

Вычислить неопределенный интеграл

.

 

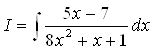Решение

 

Сделав замену переменной

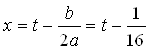
Получим

.

 

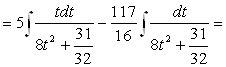
Задача 35

Вычислить .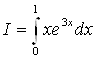

Решение

 

Полагаем , ; тогда , .

Интегрируя по частям, находим

.

 

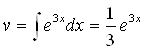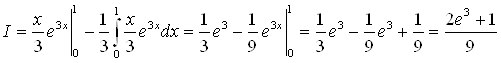Задача 36

Вычислить

.

 

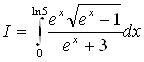Решение

 

Положим . Подстановка значений  и  в уравнение дает  и . Таким образом,

.

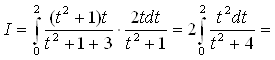
Задача 37

 

Найти .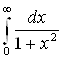

 

Решение

 

По определению

.

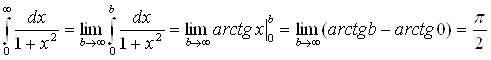Задача 40

Найти общее решение уравнения .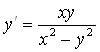

 

Решение

 

Так как

,

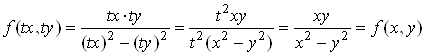то данное уравнение есть однородное дифференциальное уравнение. Заменив в исходном уравнении , получим уравнение  или .

Это уравнение с разделяющимися переменными. Разделив их, получим

,

.

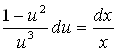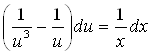Проинтегрировав последнее уравнение, найдем

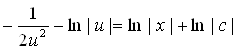 или .

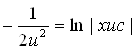Подставив 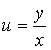, общее решение исходного уравнения запишем в виде 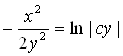, а после преобразования .

Задача 38

Найти область сходимости степенного ряда

.

 

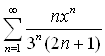Решение

Составим ряд из абсолютных величин

,

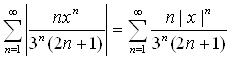По признаку Даламбера имеем:

,

следовательно 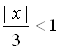, , , и на интервале  ряд сходится.

Проверим его сходимость на концах интервала:

1) Пусть . Тогда 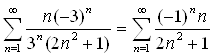 - знакочередующийся ряд. Для его анализа применим теорему Лейбница:

 

Задача 14

Вычислить 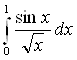 с точностью до .

 

Решение

 

Разложив в ряд  и поделив почленно на , получим:

.

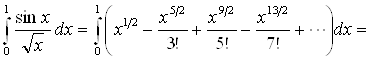
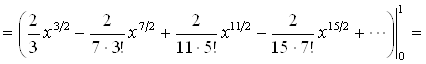
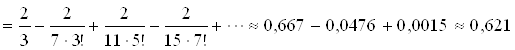Выбираем функцию  такой, чтобы .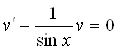

Тогда .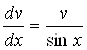

Интегрируем и находим 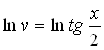 или .

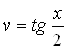Подставив найденную функцию в (1), получим ещё одно уравнение

, , ; .

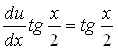Следовательно, 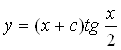 - общее решение заданного уравнения.

Задача 42

Найти общее решение дифференциального уравнения:

.

 

Решение

 

Составим характеристическое уравнение

. Так как  и , то общим решением будет

.

Частное решение неоднородного уравнения  подбирается в зависимости от вида функции .

1.  Пусть , , представляет собой многочлен степени  с действительными коэффициентами. Тогда частное решение следует искать в виде:

,

где  - многочлен той же степени, что и многочлен , но с неизвестными коэффициентами, а  - число корней характеристического уравнения, равных нулю.

Задача 43

Найти общее решение уравнения .

 

Решение

 

Ищем общее решение в виде , где  - общее решение соответствующего однородного уравнения,  - частное решение неоднородного уравнения. Так как  - многочлен первой степени  и один корень характеристического уравнения  , то частное решение надо искать в виде

.

Подберем коэффициенты  и  так, чтобы решение  удовлетворяло данному уравнению

,

,

.

Приравняв коэффициенты при одинаковых степенях левой и правой частей тождества, получим

Следовательно, 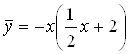, а 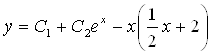 - искомое общее решение.

2.  Пусть . Тогда частное решение неоднородного уравнения , где  - число корней характеристического уравнения, равных .

Задача 44

Найти общее решение уравнения .

 

Решение

 

Ищем решение в виде . Решим однородное уравнение . Корни характеристического уравнения  равны и . Следовательно, . Частное решение ищем в виде  (так как , ). Найдем , а . Подставляя ,  и  в исходное уравнение, получим

,

, , .

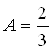Значит, 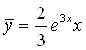- частное решение, а  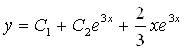- общее решение.

3.  Правая часть , где , ,  - заданные действительные числа. В этом случае частное решение ищется в виде

,

где:  и - неизвестные коэффициенты;

 - число корней характеристического уравнения, равных .

Задача 45

Найти общее решение уравнения .

 

Решение

Ищем общее решение в виде . Имеем:

, , , ,

значит, . Функция , поэтому  не совпадает с корнями характеристического уравнения . Следовательно,

,

.

Подставив ,  и  в данное уравнение, получим

.

Приравняв коэффициенты при  и , найдем

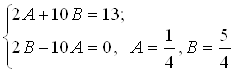
Значит, 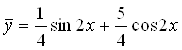 - частное решение, а

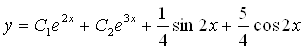 - общее решение уравнения.

 

Задача 46

Исследовать сходимость ряда .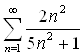

Решение

 

Найдем :

,

следовательно, исходя из необходимого признака, ряд расходится.

 

Задача 47

Исследовать сходимость ряда

 

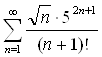
Решение

 

Применим признак Даламбера:

,

,

,

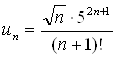следовательно, ряд сходится.

Задача 48

Исследовать на сходимость ряда

.

 

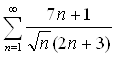Решение

 

Сравним данный ряд с рядом :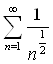

.

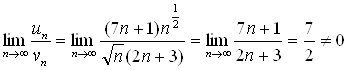матрица задача алгебраическая ряд уравнение

Следовательно, оба ряда ведут себя одинаково. Ряд 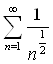 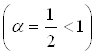 расходится , следовательно, и данный ряд  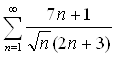тоже расходится.

Размещено на http://www.