Навигация
Синтез частотных характеристик линейных систем автоматического регулирования
ФЕДЕРАЛЬНОЕ АГЕНТСТО ПО ОБРАЗОВАНИЮ РФ
РЯЗАНСКИЙ ГОСУДАРСТВЕННЫЙ РАДИОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра РТС
«Синтез частотных характеристик линейных систем автоматического регулирования»
Выполнил ст. гр. 511
Шмелёв А.О.
Проверил
Гришаев Ю.Н.
Рязань 2008
Задание
логарифмическая частотная разомкнутая система
1. Построить логарифмические частотные характеристики разомкнутой системы по заданным показателям качества.
2. Определить по построенным ЛАХ и ЛФХ запасы устойчивости по усилению и по фазе.
3. Записать передаточную функцию разомкнутой системы по построенной ЛАХ.
4. Рассчитать и построить АЧХ замкнутой системы.
Исходные данные
1. Постоянная ошибка: по укорению (δст/х0)·102=0,5
2. Частота среза: ωср(2+n)·10-2=3, где n=1
3. Логарифмический коэффициент передачи L01 на частоте 0.1ωср не менее 26дБ.
4. Запас устойчивости по фазе Δφ±100=400
5. Постоянные времени обязательных инерционных звеньев: Тин1·104=7, Тин2·105=3
6. Частота гармонической помехи (ωп/ωср)·10-2=3
7. Коэффициент подавления помехи Lп не менее 80дБ
Построение ЛАХ и ЛФХ разомкнутой системы
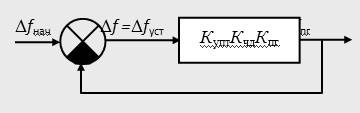
Построение ЛАХ начинается с низкочастотной асимптоты. Т.к. задана статическая ошибка то система будет статической , наклон ЛАХ для низкочастотной асимптоты будет нулевым и ошибка определяется выражением δст= х0/(1+k).
(δст/х0)·102=0,5=> δст/х0=0,5*10-2 – относительная ошибка
k= х0 / δст -1 =2*102 -1=199 - коэффициент передачи разомкнутой системы
L1=20lg(k)=20lg(199)=46 – логарифмический коэффициент передачи разомкнутой системы
Т.е. низкочастотная асимптота проводится через т.(1;46) параллельно оси частот.
Для обеспечения требуемого запаса устойчивости по фазе требуется, чтобы ЛАХ пересекала ось частот под наклоном -20дБ/дек на частоте среза.
ωср(2+n)·10-2=3=> ωср=300/3=100 рад/с
Построенные участки ЛАХ соединяются прямой линией под наклоном -40дБ/дек, при этом для обеспечения п.3 исходных данных выбираем ωс1=5рад/с, тогда т.(10;26) (т. (0.1 ωср ;L01)) пройдёт ниже прямой с нулевым наклоном.
Сопрягающую частоту ωс2 выбираем из условия запаса устойчивости по фазе Δφ±100=400 (т.к. последующие типовые и обязательные инерционные звенья будут вносить дополнительный фазовый сдвиг): ωс2= ωср /2=50 рад/с .
Построенная ЛАХ сформирована последовательным соединением следующих типовых звеньев: безынерционным k(p)=199, двумя инерционными k(p)=1/(1+Т1р)2 и форсирующим k(p)=(1+ Т2p). Т.о. передаточная функция соединения типовых звеньев будет иметь вид:
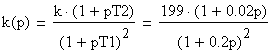
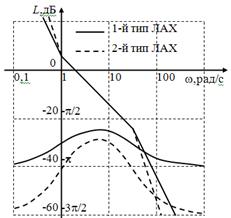
ЛФХ полученной передаточной функции строится сложением ЛФХ отдельных звеньев.
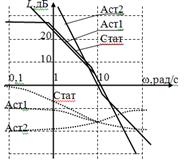
Из рис видно, что при соединении таких типовых линейных звеньев, ЛФХ системы не попадает в заданный интервал устойчивости по фазе. Для обеспечения этого условия в систему вводится дополнительное инерционное звено с сопрягающей частотой ωс3 лежащей выше частоты среза. Система с дополнительным инерционным звеном будет проходить внутри заданного интервала при ωс3=333рад/с .
Достраиваем ЛАХ и ЛФХ системы с учетом введенного звена, обязательных инерционных звеньев, п.5 исходных данных, и проверяем требование к подавлению гармонической помехи п.6 и п.7 исходных данных:
Тин1·104=7 => Тин1=7·10-4с => ωин1=1/Тин1=1.43·103рад/с
Тин2·105=3 => Тин2=3·10-5с => ωин2=1/Тин2=3.3·103рад/с
(ωп/ωср)·10-2=3 => ωп=ωср·3·102=100·3·102=30·103рад/с
Lп ≥ 80дБ
На рис видно, что т.( 30·103;-80) лежит выше ЛАХ разомкнутой системы, следовательно, требование к подавлению гармонической помехи выполняется.
Определение запасов устойчивости
Проведем графически по построенным ЛАХ и ЛФХ разомкнутой системы.
Запас устойчивости по усилению ΔL=24дБ.
Запас устойчивости по фазе Δφ=450.
Запись передаточной функции разомкнутой системы по асимптотической ЛАХ
При частотах близких к 0 ЛАХ имеет нулевой наклони, значит, формируется безынерционным звеном с передаточной функцией k(p)=k. На ωс1 наклон изменяется на – 40 дб/дек – этот наклон обеспечивается 2 инерционными звеньями с k(p)=1/(1+Т1р)2 , Т1=1/ ωс1 . С таким наклоном ЛАХ идёт до ωс2 , а потом наклон становится равным – 20 дб/дек. Изменение наклона на + 20 дб/дек обеспечивается форсирующим звеном с k(p)=(1+Т2р), Т2=1/ ωс2 . На ωс3 наклон изменяется на - 20 дб/дек и становится равным - 40 дб/дек, т. е. действует инерционное звено с k(p)=1/(1+Т3р). На ωин1 наклон изменяется на - 20 дб/дек и становится равным - 60 дб/дек, т. е. действует инерционное звено с k(p)=1/(1+Тин1р). На ωин2 наклон изменяется на - 20 дб/дек и становится равным - 80 дб/дек, т. е. действует инерционное звено с k(p)=1/(1+Тин2р).
При построении ЛАХ разомкнутой системы использовались типовые линейные звенья, поэтому передаточная функция этой системы может быть записана как совокупность таких звеньев.
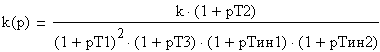 ,
,
где k=199
Т1=1/ωс1=1/5=0.2с,
Т2=1/ωс2=1/50=0.02с,
Т3=1/ωс3=1/333=0.003с,
Тин1=7·10-4с,
Тин2=3·10-5с.
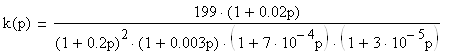
Расчет АЧХ замкнутой системы
Амплитудно-частотная характеристика замкнутой системы связана с частотными характеристиками разомкнутой следующим соотношением:
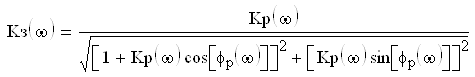
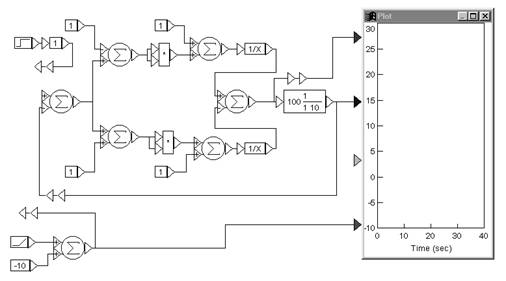
АЧХ и ФЧХ разомкнутой системы можно найти двумя путями. Во-первых, по построенным J1AX и ЛФХ разомкнутой системы и, во-вторых, по комплексной частотной характеристике разомкнутой системы.
Первый способ: По ЛАХ находим значения Lp(ω) в диапазоне от 24 до 450рад/с, по ЛФХ находим значения φр(ω) в этом же диапазоне. Переходим от логарифмического коэффициента передачи к обычному
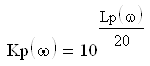
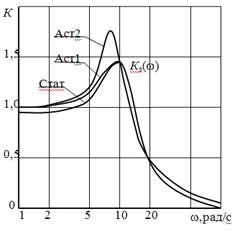
и строим АЧХ замкнутой системы по значениям Кз(ω)
| ω | 24 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 200 | 300 | 400 | 450 |
| Lp(ω) | 20 | 15 | 10 | 6 | 4 | 3 | 2 | 1 | 0 | -6 | -9 | -15 | -20 |
| Кр(ω) | 10 | 5.6 | 3.2 | 1.9 | 1.5 | 1.4 | 1.3 | 1.1 | 1 | 0.5 | 0.4 | 0.17 | 0.1 |
| φр(ω) | -140 | -144 | -143 | -140 | -140 | -140 | -135 | -135 | -135 | -140 | -153 | -162 | -171 |
| Кз(ω) | 1.1 | 1.16 | 1.29 | 1.46 | 1.53 | 1.55 | 1.41 | 1.35 | 1.3 | 0.7 | 0.6 | 0.2 | 0.1 |
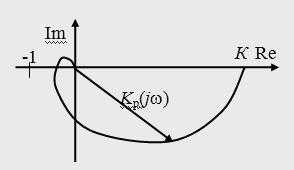
Второй способ: Подставим в передаточную функцию разомкнутой системы p=jω, получим комплексную частотную характеристику
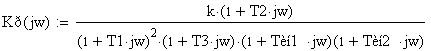
её модуль будет равен:
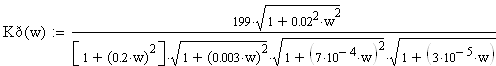
ФЧХ ![]()
| ω | 24 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 200 | 300 | 400 | 450 |
| Кр(ω) | 9.2 | 6.2 | 3.9 | 2.8 | 2.1 | 1.7 | 1.4 | 1.2 | 1.1 | 0.44 | 0.25 | 0.16 | 0.13 |
| φр(ω) | -135.9 | -136.5 | -135.6 | -134.2 | -133 | -132.2 | -131.7 | -131.6 | -131.7 | -140.5 | -151.9 | -162.2 | -166.8 |
| Кз(ω) | 1.1 | 1.13 | 1.19 | 1.26 | 1.32 | 1.35 | 1.33 | 1.3 | 1.28 | 0.6 | 0.32 | 0.2 | 0.15 |

Генерирование независимых случайных процессов
Похожие работы
... Рис. 6 Рис. 7 Схема моделирования показана на рис. 8. Рис.8 Исследование устойчивости для удобства сравнения проводится на трех моделях, отличающихся структурой или параметрами. 2.Оптимальные линейные САР Задача оптимального синтеза линейной системы авторегулирования при случайных воздействиях заключается в определении такой структуры и параметров системы, при ...
... уравнений и даже не определении выходного процесса по заданному входному. Хотя это достаточно важный для теории автоматического управления вопрос, основной целью настоящего раздела является введение центрального для классической теории понятия частотной характеристики и, далее, передаточной функции. Затем, с использованием этих понятий можно обсудить вопросы определения выходного процесса по ...
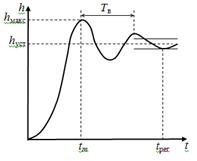
... частот, то переходная характеристика будет колебательной. Переходная характеристика является показателем качества при быстро изменяющемся воздействии. Для систем авторегулирования лучшей считается колебательная переходная характеристика с быстрым затуханием колебаний на вершине (рис. 4). Рис. Обычно используются следующие числовые параметры переходной характеристики: время достижения ...
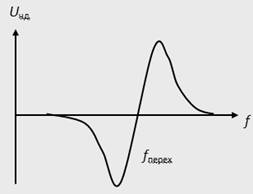
... характеристик системы в установившемся режиме составляется статическая модель. В ней отражаются только функциональные преобразования процессов. Статическая модель системы изображена на рис. 4. При ее составлении учитывалось, что для постоянного воздействия коэффициент передачи ФНЧ равен 1, а частота перестраиваемого генератора fп г = fпг0 + Dfпг, где fпг0 – частота ПГ при управляющем ...

0 комментариев