Навигация
Формула повної ймовірності. Формула Байєса
13385
знаков
0
таблиц
0
изображений
3. Формула повної ймовірності. Формула Байєса
Нехай подія 
може статися за умови появи однієї з несумісних подій (гіпотез) 
,
, ... ,
, що створюють повну групу. Тоді ймовірність події обчислюється за формулою повної ймовірності:
,
де 
– ймовірність гіпотези 
; 
– умовна ймовірність події за умови, що подія відбулася.
Якщо до експерименту ймовірності гіпотез були 
а внаслідок експерименту відбулася подія , то з урахуванням цієї події "нові", тобто умовні, ймовірності гіпотез обчислюються за формулами Байєса:
.
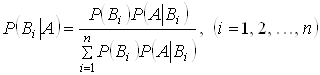Формули Байєса дають можливість "переглянути" ймовірності гіпотез з урахуванням результату експерименту, що спостерігався.
Приклад.На склад надходить продукція трьох фабрик, причому продукція першої фабрики становить 20%, другої – 46%, третьої – 34%. Відомо також, що середній процент нестандартних деталей для першої фабрики дорівнює 3%, другої – 2%, третьої – 1%.
1. Знайти ймовірність того, що вибрана навмання деталь буде нестандартною.
2. Знайти ймовірність того, що деталь виготовлена на першій фабриці, якщо вона виявилася нестандартною.
3. Знайти ймовірність того, що деталь виготовлена на другій фабриці, якщо вона виявилася стандартною.
Розв’язок.
1. Вибрана навмання деталь може бути виготовлена або на першій фабриці (подія ) або на другій (подія ) або на третій (подія 
). Події несумісні і складають повну групу. Ймовірності подій дані в умові задачі:
.
В умові задані й умовні ймовірності. Ймовірність того, що навмання вибрана деталь буде нестандартною (подія ) за умови, що деталь виготовлена на першій фабриці (подія ): 
. Аналогічно, 
; 
.
Подія (навмання вибрана деталь буде нестандартною) може відбутися тільки разом з однією з несумісних подій з повної групи, тому повну ймовірність події визначимо за формулою повної ймовірності:
.
2. Відомо, що подія вже відбулася, потрібно знайти післядослідну ймовірність гіпотези . За формулою Байєса знаходимо:
.
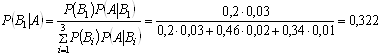3. Деталь виявилася стандартною, тобто в прийнятих нами позначеннях відбулася подія 
. Знайти післядослідну ймовірність події . За формулою Байєса:
Події (навмання вибрана деталь – нестандартна), (навмання вибрана деталь – стандартна) протилежні, тому
.
Аналогічно обчислюється 
:
.
Підставляючи обчислені значення у формулу, отримаємо:
.
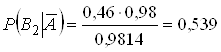Похожие работы
... аксіоматичного визначення поняття ймовірності П.Л. Чебишев (1821–1894 р.) був творцем і ідейним керівником петербурзької математичної школи. Чебишев зіграв велику роль у розвитку багатьох розділів математики, у тому числі теорії ймовірностей. У своїй магістерській дисертації в першому розділі він уводить поняття ймовірності. Для цього він, насамперед, визначає рівно можливі події: «Якщо з ...
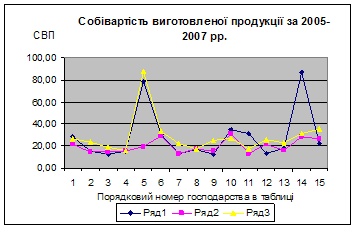
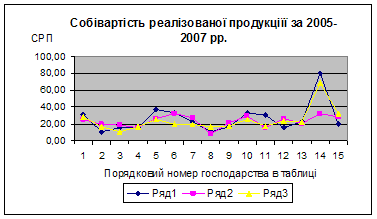
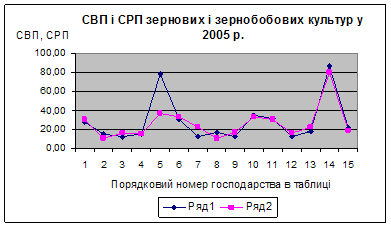
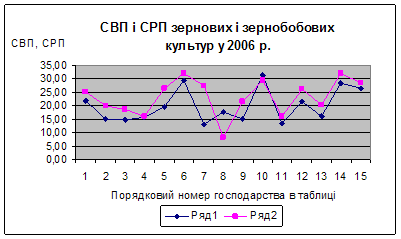
... змін, спостерігається тільки нестабільність та по деяких господарствах різкі зміни собівартості продукції, що виготовляється та реалізується. 3. Економіко-математичне моделювання в управлінні підприємством 3.1 Економіко-математичне моделювання урожайності сільськогосподарської продукції методом Брандона. Нехай економіко-математична модель матиме вид: , Де =; =; = ; Y - ...
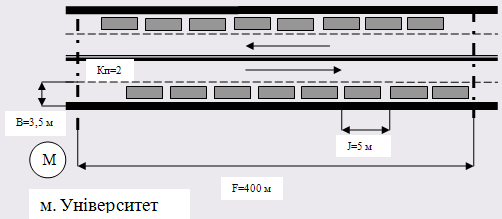
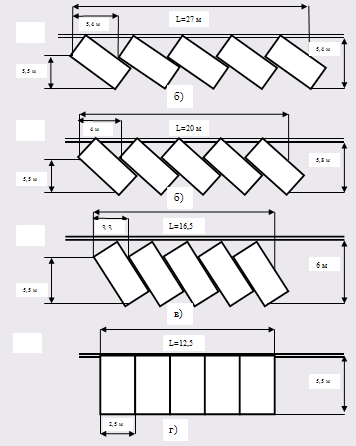
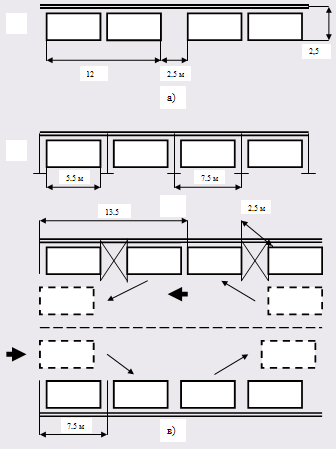
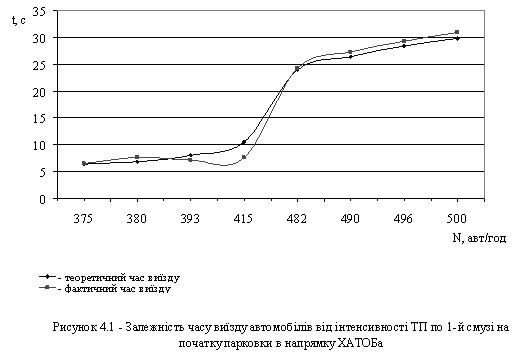
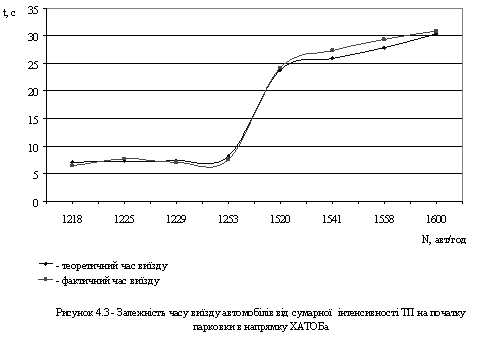
... наслідок, автомобілі припарковані уздовж проїзної частини, зменшують її ефективну ширину, що, в свою чергу, веде до збільшення заторів на дорогах, зниження швидкості руху й зменшення пропускної здатності ВДМ. Все це спричиняє зростання дорожньо-транспортних пригод і виникнення проблем екологічного, соціального й економічного характеру. Серед проблем, породжених автомобілізацією, проблеми організац ...
... заційної реструктуризації. Щоб більш результативно запобігати банкрутству, необхідно вирішити завдання запровадження ефективних, адаптованих до вітчизняних умов, механізмів визначення ймовірності банкрутства ще до виникнення явних ознак неплатоспроможності підприємства, а також створити відповідну систему моніторингу роботи підприємств на рівні регіонів. Аналіз літератури показує, що у даний час ...
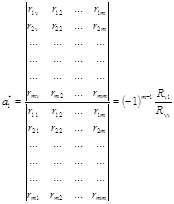
0 комментариев