Компьютерное моделирование

5. Компьютерное моделирование

Разрабатываемые компьютерные модели ТП могут использоваться в производстве путем применения микропроцессорных систем управления и контроля (МСКУ).

Функционирование МСКУ осуществляется на основе, какой-то модели, отражающей основные физические и химические процессы, протекающие в продукте. На основании модели построен алгоритм и схема управления процессом.

МСКУ обеспечивает выполнение следующих функций:

-  определение момента готовности продукта;

-  управления органами машины (оборудованием);

-  регулирование режимов (одно-, двух- или многоскоростной);

-  выдача рекомендаций (или управление) по дозировке рецептурных компонентов, воды и ее температуре).

Система уравнений, связывающих функции отклика с влияющими факторами, называется математическим описанием процесса. Метод полного факторного эксперимента дает возможность получить описание процесса в виде отрезка ряда Тейлора, имеющего вид:

Y = В0 + В1Х1 + В2Х2 + ... + Вn Хn + B1.2 Х1Х2 – ... – В (n – 1)n Х (n – 1),

Его называют уравнением регрессии, а входящие в него характеристики - коэффициентами регрессии, где Х1, ..., Хn - независимые переменные величины, влияющие на протекание процесса, называемые факторами (температура, давление, состав реакционной смеси и т.п.): Y - величина, показывающая производительность оборудования, себестоимость продукции и т.п., называемая функцией отклика. Все возможные неповторяющиеся комбинации варьирования факторов позволяет спланировать матрица полного двухфакторного эксперимента (табл. 2.1).

Таблица 2.1. Матрица полного двухфакторного эксперимента

Номер опыта	Факторы		Функция отклика
	Х1	Х2
1 2 3 4	-1 +1 -1 +1	-1 -1 +1 +1	Y1 Y2 Y3 Y4

Примечание. Здесь и далее в таблице: «-» - минимальное, «+» - максимальное значение факторов.

На основании полного двухфакторного эксперимента вычисляют коэффициенты регрессии:

B0 = 1/4 (Y1 + Y2 + Y3 + Y4),

B1 = 1/4 (-Y1 + Y2 – Y3 + Y4),

B2 = 1/4 (-Y1 – Y2 + Y3 + Y4).

Допуская значимость коэффициентов регрессии и адекватность уравнения при доверительной вероятности 0,95 и трех степенях свободы, по величине коэффициентов и их значению определяют ранжирование влияния факторов X1 и Х2 на функцию отклика Y.

Количество опытов полного факторного эксперимента для выбора социально ориентированного технологического решения резко возрастает с увеличением количества факторов. Однако для нахождения коэффициентов регрессии не всегда требуется много опытов. В таких случаях можно уменьшить объем экспериментальных работ, воспользовавшись методом дробных реплик. Этот метод заключается в нахождении математического описания процессов в определенной части полного факторного эксперимента: 1/2, 1/4 и т.д. Такие системы опытов называются дробными репликами.

Тогда матрица полного трехфакторного эксперимента и его дробных реплик будет иметь вид (табл. 2.2).

Таблица 2.2. Матрица полного трехфакторного эксперимента и его дробных реплик

Номер опыта	Факторы			Функция отклика Y	Дробные реплики
	X1	X2	X3
1	-1	-1	-1	Y1	¼
2	+1	-1	-1	Y2	½
3	-1	+1	-1	Y3	¼
4	+1	+1	-1	Y4
5	-1	-1	+1	Y5	¼
6	+1	-1	+1	Y6	½
7	-1	+1	+1	Y7
8	+1	+1	+1	Y8	¼

Расчет коэффициентов регрессии, проверка их значимости и адекватности математического описания в данном случае производятся так же, как и при полном факторном эксперименте, например в виде уравнения регрессии:

Y = B0 + B1X1 + B2X2 + B3X3.

Если для вычисления коэффициентов регрессии воспользоваться полным трехфакторным экспериментом, то необходимо провести 8 опытов. Однако эту задачу можно решить и с помощью двухфакторного эксперимента, если в матрице приравнять произведение X1 Х2 к фактору Х3 (табл. 2.3).

Таблица 2.3. Упрощенная матрица

Номер опыта	Факторы				Функция отклика Y
	X1	Х2	Х1 Х2	Х3
1	-1	-1	+1	+1	Y1
2	+1	-1	-1	-1	Y2
3	-1	+1	-1	-1	Y3
4	+1	+1	+1	+1	Y4

Коэффициенты регрессии вычисляют по следующим формулам:

B0 = ¼(Y1 + Y2 + Y3 + Y4), B1 = ¼(-Y1 + Y2 – Y3 + Y4),

B2 = ¼(-Y1 – Y2 + Y3 + Y4).

Коэффициент В3 не может быть определен раздельно, поэтому вычисляем сумму:

B1,2 + B3 = ¼(Y1 – Y2 – Y3 + Y4),

тогда искомое уравнение будет иметь вид:

Y = B0 + B1X1 + B2X2 + (B1,2 + B3)X3.

При выборе социально ориентированной технологии переработки сырья с точки зрения экономики и экологии можно быстрее получить результат с помощью ПК.

В процессе выполнения исследований необходимо также вычислить коэффициент корреляции, который рассчитывается по формуле:

где YiВ , YiР - значение первого виртуального (В) и второго реального (Р) показателей;

n - размер элементов в выборке (число корреляционных пар).

При необходимости рассчитывается достоверность коэффициента корреляции. Если по величине абсолютного значения μ степень корреляционной зависимости между показателями менее 0,4 - зависимость слабая; 0,4-0,59 - средняя; 0,6-0,78 - значительная; более 0,8 - высокая.

При моделировании производства функциональной продукции с использованием ПК необходимо виртуально предположить процессы и выявить их закономерности для последующего практического использования этих зависимостей в реальных производственных условиях конкретного производства. Следовательно, необходимо осуществить регулирование технологического процесса с учетом СМС путем их моделирования в виртуальных условиях на основе методов ИР.

6. Экологизация технологического процесса

Проблема окружающей среды и рационального использования природных ресурсов является одной из наиболее актуальных общечеловеческих проблем, так как от ее решения зависит жизнь на земле, здоровье и благосостояние человечества.

Вокруг предприятия предусмотрена санитарно-защитная зона шириной 50 м. Эта зона озеленена и благоустроена. Зеленые насаждения обогащают воздух кислородом, поглощают углекислый газ, шум, очищают воздух от пыли и регулируют микроклимат.

Загрязнение атмосферного воздуха и водоемов находится в пределах допустимых норм, так как с этой целью предусмотрены очистные сооружения.

После промывки оборудования и инвентаря вода, содержащая загрязнения сливается через отверстия в полу, которые связаны с канализацией, сточные воды обрабатываются на очистных сооружениях, а образовавшиеся осадки используются для реализации как удобрения в сельском хозяйстве. Очищенная вода на предприятии используется повторно, но только в бытовых целях.

Заключение

В курсовой работе была рассмотрена технологическая линия производства яблочного сока на малых предприятиях.

В ходе работы были достигнуты следующие цели:

1. ознакомился с характеристикой сырья, выявил лучшие сорта яблок для наиболее лучшего качества соков. Ознакомился с химическим составом яблок.

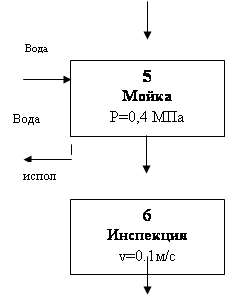
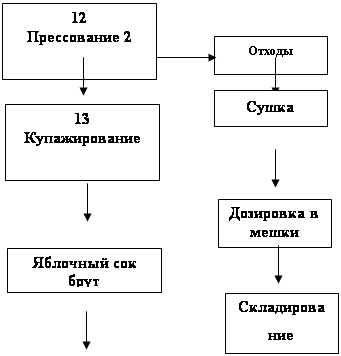
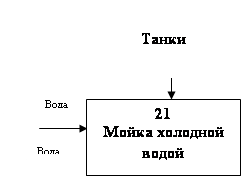
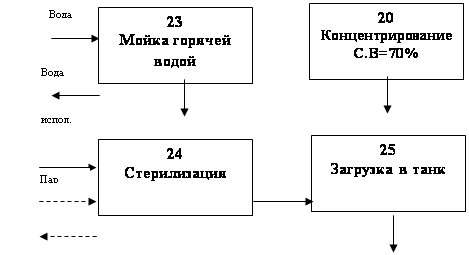
2. Разработал конструкторно-технологические схемы производства яблочного сока, создал технологическую схему производства яблочного сока и операторную схему.

3. Произвёл продуктовый расчет, определил массу сырья, готовой продукции, отходов и потерь по технологической схеме производства. Определил производительную мощность линии.

4. Подобрал и рассчитал технологическое оборудование, определил число машин (аппаратов) их размеры и основные конструктивные элементы.

5. Произвёл компьютерное моделирование, ознакомился с методами решения основных уравнений, алгоритмов их реализации и компьютерных программ.

6. Ознакомился с экологизацией технологического процесса, ознакомился с рациональным использованием ресурсов.

Список использованной литературы

1. Общая технология пищевых производств / Под ред. А. П. Ковальской. – М.: Колос 1993–384 с.

2. Самсонова А. Н. Фруктовые и овощные соки

3. Технология консервированных плодов и овощей. А. Ф. Фан-Юнг, Б. Л. Флау менбаум, А. К. Изотов – М.: Пищевая пром-сть

4. Рогачёв В.И. Справочник технолога плодоовощного консервного производства.