Навигация
3. Кинематические цепи
Кинематические цепи по характеру относительного движения звеньев разделяются на плоские и пространственные. Кинематическая цепь называется плоской, если точки её звеньев описывают траектории, лежащие в параллельных плоскостях. Кинематическая цепь называется пространственной, если точки её звеньев описывают неплоские траектории или траектории, лежащие в пересекающихся плоскостях.
По виду звеньев, входящих в кинематические цепи, последние разделяются на простые и сложные.
Простой называется такая цепь, у которой каждое звено входит не более чем в две кинематические пары (рис.2).
Сложной кинематической цепью называется цепь, в которой имеется хотя бы одно звено, входящее более чем в две кинематические пары (рис.3).
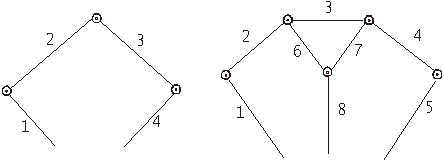
Рис.2 Рис.3
Замкнутой называется кинематическая цепь, каждое звено которой входит в две и более кинематических пар.
Незамкнутой кинематической цепью называется кинематическая цепь, в которой есть звенья, входящие только в одну кинематическую пару.
При равном числе подвижных звеньев замкнутые цепи имеют меньшее число степеней свободы, чем незамкнутые. Замкнутые цепи широко применяются в кинематических цепях рабочих машин, станков, автоматов и т.д., разомкнутые – в цепях манипуляторов и роботов.
В машинах обычно применяются такие кинематические цепи, у которых одно из звеньев неподвижно, т.е. является стойкой. Например, в механизме двигателя внутреннего сгорания кривошип, шатун, поршень и цилиндр образуют кинематическую цепь, у которой неподвижным звеном (стойкой) является цилиндр с рамой двигателя (рис.4 а,б).
Звено механизма, на которое действуют внешние силы, приводящие его в движение, называется ведущим. Звено, к которому приложены полезные сопротивления, ради преодоления которых построен механизм, называется ведомым.
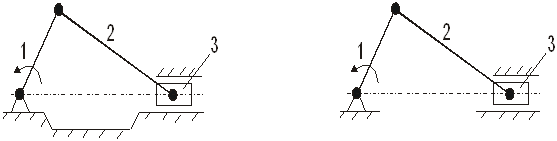
Рис.4 а Рис.4 б
При исследовании кинематики механизма, движение одного из звеньев считают заданным. Его называют входным. Звено, движение которого хотят определить в зависимости от движения входного, называют выходным. В нашем примере ползун – выходное звено, кривошип –входное.
4. Степень подвижности плоской кинематической цепи
кинематический пар цепь плоский механизм
Каждое свободное тело при плоскопараллельном движении обладает тремя степенями свободы, поэтому до соединения К-звеньев в кинематические пары они все обладали ЗК степенями свободы.
При соединении звеньев в кинематические пары последние отнимают у них определенное количество степеней свободы: пары V-го класса в плоских механизмах отнимают две степени свободы (из трех), оставляя одну; пары IV-го класса отнимают одну степень свободы, оставляя две.
Таким образом, плоская кинематическая цепь будет обладать следующим количеством свободы:
H = 3K - 2p1 - p2
Если одно звено кинематической цепи сделать неподвижным, то число степеней свободы уменьшится еще на три и относительно неподвижного звена будет равно:
W = H – 3 или W=3(k-1) - 2p1 - p2
Обозначая k – 1 = n (количество подвижных звеньев), окончательно получим:
W = 3n - 2p1 - p2
где:
n – число подвижных звеньев кинематической цепи;
p1 - число высших пар (накладывающих по одному условию связи);
p2 - число низших пар в кинематической цепи (накладывающих по два условия связи).
Так, кинематическая цепь двигателя имеет 3 подвижных звена, 3 пары вращения и 1 поступательную пару, всего 4 низших пары. Поэтому для нее
W = 3·3 - 2·4 =1
Число степеней свободы кинематической цепи относительно неподвижного звена W называется степенью подвижности кинематической цепи.
Формула для определения степени подвижности кинематической цепи была впервые получена известным русским ученым П.Л.Чебышевым в 1869 г. и носит его имя. Эта формула пригодна только для плоских кинематических цепей.
Задаваясь различными сочетаниями этих чисел, можно получить группы различного вида. Все получаемые таким способом группы можно разбить по классам.
Рассмотрим структурную классификацию плоских механизмов.
Назовем условно ведущее звено и стойку, образующие кинематическую пару V класса, механизмом I класса(рис.5).
Образование любого плоского механизма может быть представлено как последовательное присоединение групп звеньев, удовлетворяющих условию W = 0, к начальному механизму.
ведущее звено ведущее звено

Например, первая группа (рис.6.а) присоединяется к одному механизму I класса (ведущему звену и стойке), следующая группа – либо к звеньям первой группы, либо частично к звеньям первой группы и ведущему звену или к стойке и т.д.
Механизмы, образованные присоединением нескольких групп к механизму I класса, так же как и сам он, обладают степенью подвижности, равной единице, так как группы не изменяют степени подвижности механизма, к которому они присоединяются.
Механизмы могут быть образованы также и присоединением групп одновременно к нескольким механизмам I класса (рис .6.б). В этих случаях степень подвижности получаемых механизмов будет равна числу механизмов I класса, к которым производится такое присоединение групп, т.е. числу ведущих звеньев полученного механизма.
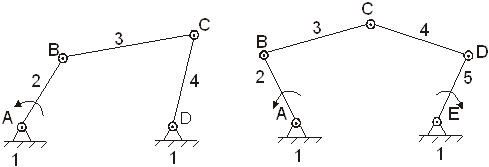
а) 2 - ведущее звено б) 2 и 5 – ведущие звенья
Рис. 6
Группа звеньев (рис.7), имеющая два звена и три пары V класса, называется группой II класса второго порядка или двухповодковой группой Ассура. (Присоединение этой группы к основному механизму производится двумя поводками ВС и CD).
Порядок группы определяется числом элементов, которыми группа присоединяется к основному механизму.
Механизмы, в состав которых входят группы классов не выше второго, называются механизмами II класса.
Группа, содержащая два звена и три вращательные пары, называется первым видом группы II класса.
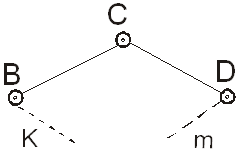
Рис.7
Все последующие виды группы II класса могут быть получены путем замены отдельных вращательных пар парами поступательными.
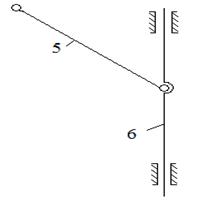
Вторым видом является тот вид, при котором поступательной парой заменена одна из крайних вращательных пар (рис.8).
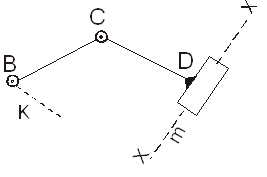
Рис. 8
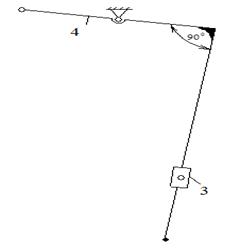
Третий вид – поступательной парой заменена средняя вращательная пара (рис.9).
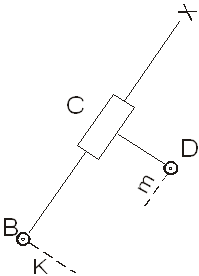
Рис.9
Четвертый вид – две крайние вращательные пары заменены двумя поступательными парами (рис.10).
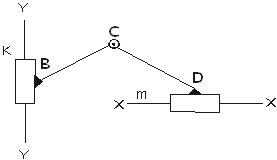
Рис.10
Пятый вид – поступательными парами заменены крайняя и средняя вращательные пары (рис.11).
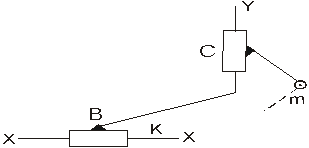
Рис.11
Таким образом, в плоских механизмах с вращательными, поступательными и высшими парами IV и V классов имеется пять групп II класса. Большинство современных механизмов, применяемых в технике, принадлежит к механизмам II класса.
Рассмотрим теперь второе возможное сочетание чисел звеньев и кинематических пар. Следующая по числу звеньев группа должна содержать четыре звена и шесть пар V класса (рис.12). Для этого сочетания могут быть получены три типа кинематических цепей, структурные принципы образования которых различны.
Первая кинематическая цепь представляет собой более сложную незамкнутую кинематическую цепь и является группой III класса третьего порядка и называется трехповодковой группой.
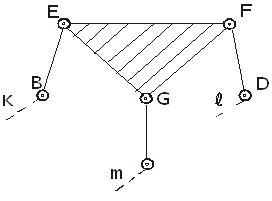
Рис.12
Звено EFC – базисное звено.
Механизмы, в состав которых входят группы не выше групп III класса третьего порядка, называются механизмами III класса (рис.13).
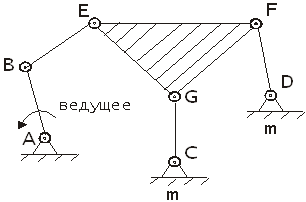
Рис.13
Вторая кинематическая цепь – замкнутая кинематическая цепь, которая присоединяется к звеньям «k» и «m» основного механизма не элементами поводков, а свободными элементами B и G, принадлежащими базисными звеньями (рис.14).
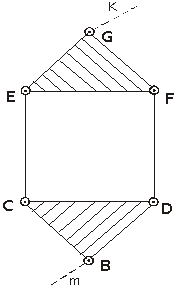
Рис.14
Данная группа кроме двух базисных звеньев BCD и EGF, образующих два жестких замкнутых контура, имеет один подвижный четырехсторонний замкнутый контур CEFD (рис.15).
Группы, в состав которых входят подвижные четырехсторонние замкнутые контуры, относят к группам IV класса.
Третий вид кинематической цепи: эта цепь распадается на две простейшие группы II класса – BCD и EFG – и потому относится к уже ранее рассмотренным и не представляет ничего принципиально нового (рис.16).
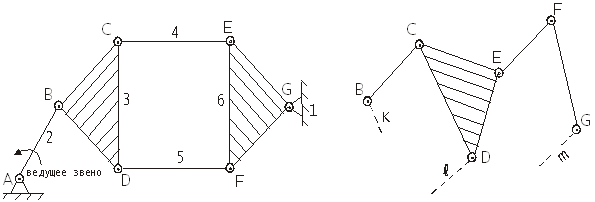 Рис. 1.15 Рис.1.16
Рис. 1.15 Рис.1.16
Следовательно, в состав группы II класса входит односторонний контур, в группу III класса – трехсторонний замкнутый контур, в группу IV класса замкнутый четырехсторонний контур. Все рассмотренные группы получаются соответствующими изменениями структуры контуров.
ЛИТЕРАТУРА
1. Артоболевский И.И. Теория механизмов и машин. М, 1975, с.48-90.
2. Кореняко А.С. и др. Курсовое проектирование по теории механизмов и машин. Киев,1970, с.11-15.
Похожие работы
... е. число неизвестных параметров реакций должно быть равно количеству уравнений статики, которые можно составить для их определения. Начинать силовой анализ необходимо с наиболее удаленной от ведущего звена структурной группы. 3.1 Определение реакций в кинематических парах структурных групп Чтобы определить величины и направления сил инерции, надо знать ускорения и массы звеньев. Ускорения ...
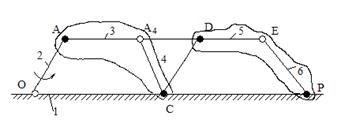
... для него план механизма. Построили диаграмму усилий, действующее на исполнительное звено, и если необходимо, построили 2 плана положений соответствующие началу и концу действия сил полезного сопротивления. Структурный анализ механизма 1. Выписываем кинематические пары определяя класс и вид 1–2 – вращ., 5 кл 2–3 – вращ., 5 кл 3–4 – поступ., 5 кл 4–1 – вращ., 5 кл 4–5 – вращ., 5 кл 5–6 – ...
... механизма для обеспечения эффективного перехода на различные способы транспортирования в зависимости от свойств материала и выполняемой технологической операции. Разработке методов кинематического анализа механизмов транспортирования ткани швейных машин и соответствующего этой задаче алгоритмического и программного обеспечения посвящены работы. [67],[71],[72]. В работе Ю.Ю.Щербаня и В.А.Горобца ...
... трением качения: а) платформа на катках (рис. 6.8) : f' = (k1 + k2 )/d ; (6.6) б) подшипник качения (рис. 6.9) : T = 0.5*Q*fs*d1; f' = beta*k* (1+ d1/d3) /d1 ; (6.7) для реальных конструкций подшипников beta = 1.4 - 1.6. 6.3. Коэффициенты полезного действия механизмов. 6.3.1. Коэффициент полезного действия - отношение полезной мощности на выходе Nn к мощности движущего усилия на ...
0 комментариев