Навигация
Определение времени полного растворения
2.4 Определение времени полного растворения
В отличие от кинетической функции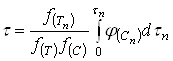 (20)
(20)
В частности, для определения времени полного растворения при некоторых фиксированных значениях ![]() и
и ![]() достаточно подставить в уравнение (20)
достаточно подставить в уравнение (20) ![]() вместо
вместо ![]() и
и ![]() вместо
вместо ![]() :
:
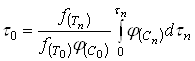 (21)
(21)
Естественно использовать для определения ![]() тот периодический опыт, для которого
тот периодический опыт, для которого ![]() . Тогда формула (21) упрощается:
. Тогда формула (21) упрощается:
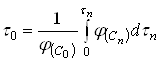 (22)
(22)
Входящий в уравнения (21) и (22) интеграл численно равен площади под кривой ![]() на рис.1. Для его вычисления можно воспользоваться любым из известных методов.
на рис.1. Для его вычисления можно воспользоваться любым из известных методов.
Таким образом, результаты периодического опыта, проведенного при изменяющейся концентрации активного реагента ![]() , позволяют легко определить время полного растворения
, позволяют легко определить время полного растворения ![]() , относящейся к постоянным значениям
, относящейся к постоянным значениям ![]() и
и ![]() . Для перехода к иным значениям концентрации и температуры можно воспользоваться соотношением, вытекающим из уравнений (20) и (21).
. Для перехода к иным значениям концентрации и температуры можно воспользоваться соотношением, вытекающим из уравнений (20) и (21).
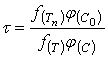 (23)
(23)
В частности, если ![]() и
и ![]() , то:
, то:
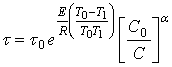 (24)
(24)
Таким образом, зная энергию активации Е, порядок реакции ![]() и время полного растворения
и время полного растворения ![]() при некоторых фиксированных значениях
при некоторых фиксированных значениях ![]() и
и ![]() по формуле (24) можно вычислить время полного растворения
по формуле (24) можно вычислить время полного растворения ![]() при любых значениях
при любых значениях ![]() и
и ![]() .
.
2.5 Рекомендации по проведению исследований и выполнению расчетов
Результаты одного лабораторного периодического опыта в принципе позволяют определить кинетическую функцию ![]() . В действительности нужно провести серию опытов в диапазоне интересующих значений концентрации активного реагента и температуры. Это необходимо для обеспечения надежности кинетических величин.
. В действительности нужно провести серию опытов в диапазоне интересующих значений концентрации активного реагента и температуры. Это необходимо для обеспечения надежности кинетических величин.
Кроме того, проведение серии опытов необходимо для экспериментального подтверждения инвариантности кинетической функции относительно концентрации и температуры.
Результатом такой серии опытов будет совокупность кривых ![]() . Из каждой кривой нужно определить кинетическую функцию, вычислив для ряда значений
. Из каждой кривой нужно определить кинетическую функцию, вычислив для ряда значений ![]() соответствующие значения х по формуле (18). Из этой формулы следует, что для расчета нужно знать время полного растворения
соответствующие значения х по формуле (18). Из этой формулы следует, что для расчета нужно знать время полного растворения ![]() в периодическом опыте и иметь достаточно надежные данные о ходе кинетической кривой во всем диапазоне значений
в периодическом опыте и иметь достаточно надежные данные о ходе кинетической кривой во всем диапазоне значений ![]() от 0 до
от 0 до ![]() .
.
 . При обработке экспериментальных данных относящихся к каждому проведенному опыту, вместо определения х по формуле (18) вычисляют значения
. При обработке экспериментальных данных относящихся к каждому проведенному опыту, вместо определения х по формуле (18) вычисляют значения  (25)
(25)
где ![]() -время, необходимое для достижения
-время, необходимое для достижения ![]() в периодическом опыте.
в периодическом опыте.
В результате такой обработки экспериментальных данных получают зависимость доли нерастворившегося компонента ![]() от безразмерного времени
от безразмерного времени
![]() при постоянных концентрации активного реагента и температуре. Нетрудно убедиться в том, что, зависимость
при постоянных концентрации активного реагента и температуре. Нетрудно убедиться в том, что, зависимость ![]() есть полный аналог кинетической функции
есть полный аналог кинетической функции ![]() . Аргументы х и
. Аргументы х и ![]() отличаются друг от друга лишь постоянным множителем.
отличаются друг от друга лишь постоянным множителем.
Действительно, из соотношений 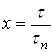 и
и  следует, что
следует, что
 (26)
(26)
где 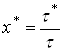 - значение безразмерного времени х, отвечающее выбранной фиксированной величине
- значение безразмерного времени х, отвечающее выбранной фиксированной величине ![]() . Соотношение (26) показывает, что зависимость
. Соотношение (26) показывает, что зависимость ![]() сохраняет присущее кинетической функции свойство инвариантности относительно условий проведения процесса (поскольку величины х и
сохраняет присущее кинетической функции свойство инвариантности относительно условий проведения процесса (поскольку величины х и ![]() не зависят от этих условий).
не зависят от этих условий).
![]()
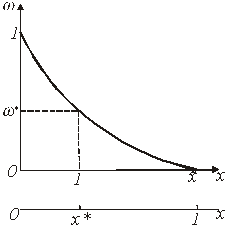
![]() Рис.2. Зависимость доли нерастворившегося компонента
Рис.2. Зависимость доли нерастворившегося компонента ![]() от безразмерного времени
от безразмерного времени ![]() .
.
На рис.2 безразмерное время ![]() пропорционально отношению
пропорционально отношению ![]() , где
, где ![]() - время, необходимое для достижения некоторого фиксированного значения
- время, необходимое для достижения некоторого фиксированного значения ![]() .
.
1. Результаты каждого периодического опыта необходимо представить в виде зависимости доли нерастворившегося компонента ![]() и концентрации активного реагента
и концентрации активного реагента ![]() от времени
от времени ![]() :
: ![]() и
и ![]() .
.
2. Выбирают некоторое фиксированное значение ![]() с таким расчетом, чтобы значению
с таким расчетом, чтобы значению ![]() от 1 до
от 1 до ![]() соответствовали достаточно надежные участки всех экспериментальных кривых.
соответствовали достаточно надежные участки всех экспериментальных кривых.
3. По уравнению (25) вычисляют значение ![]() , отвечающие ряду последовательных значений
, отвечающие ряду последовательных значений ![]() . Такие расчеты выполняют для каждого опыта.
. Такие расчеты выполняют для каждого опыта.
4. Результаты расчетов используют для получения усредненной по всем опытам зависимости ![]() . Эту зависимость удобно нанести на график вместе с результатами обработки отдельных опытов и тем самым убедиться в инвариантности функции
. Эту зависимость удобно нанести на график вместе с результатами обработки отдельных опытов и тем самым убедиться в инвариантности функции ![]() относительно технологических параметров процесса в исследованном диапазоне.
относительно технологических параметров процесса в исследованном диапазоне.
5. С помощью формулы:
 (27)
(27)
необходимо перейти к обычной кинетической функции ![]() т.е. необходимо изменить масштаб по оси абцисс (рис.2).
т.е. необходимо изменить масштаб по оси абцисс (рис.2).
Последний этап необходим для единообразия вычислительных процессов при переходе к их моделированию. Возможные значения безразмерного времени должны быть заключены в диапазон от 0 до 1. Поэтому использование кинетической функции ![]() , в которой аргумент нормирования в максимальной продолжительности процесса - времени полного растворения, предпочтительнее.
, в которой аргумент нормирования в максимальной продолжительности процесса - времени полного растворения, предпочтительнее.
Заметим, что при растворении труднорастворимых веществ и выщелачивании чаще всего не достигают стопроцентного растворения или извлечения полезного компонента. В этом случае под временем полного растворения ![]() естественно понимать время достижения максимального возможного извлечения. Если обозначить максимально возможное извлечение через
естественно понимать время достижения максимального возможного извлечения. Если обозначить максимально возможное извлечение через ![]() , то связь между долей нерастворившегося компонента и достигнутым извлечением
, то связь между долей нерастворившегося компонента и достигнутым извлечением ![]() опишется формулой:
опишется формулой:
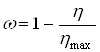 (28)
(28)
Это значит, что при определении ![]() не следует принимать во внимание ту часть полезного компонента, которая не может быть переведена в раствор. Тогда изменению
не следует принимать во внимание ту часть полезного компонента, которая не может быть переведена в раствор. Тогда изменению ![]() от 0 до
от 0 до ![]() (или х от 0 до 1) соответствует изменение
(или х от 0 до 1) соответствует изменение ![]() от 1 до 0, что также благоприятствует единообразию вычислительного процесса.
от 1 до 0, что также благоприятствует единообразию вычислительного процесса.
III. ПРОСТЫЕ МОДЕЛИ РАСТВОРЕНИЯ И ВЫЩЕЛАЧИВАНИЯ
Для подавляющего большенства процессов кинетическая функция1. Исходный продукт представляет собой совокупность сферических частиц одинакового размера, скорость растворения которых пропорциональна поверхности. В этом случае справедливо следующее дифференциальное уравнение для скорости растворения:
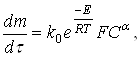 (29)
(29)
где m – масса частицы;
F – поверхность частицы;
k0 – константа скорости реакции, не зависящая от температуры;
![]() - порядок реакции;
- порядок реакции;
Е – энергия активации;
R – газовая постоянная.
Если обозначить текущий радиус растворяющейся частицы через r, а её начальный радиус через r0, получим, что ![]() , а
, а ![]() , где
, где ![]() - плотность твердой фазы. Поэтому:
- плотность твердой фазы. Поэтому:
 (30)
(30)
Если растворение протекает при постоянных концентрациях и температуре, то интегрирование дает:
 (31)
(31)
Таким образом, для рассматриваемой модели радиус растворяющейся частицы уменьшается во времени по линейному закону.
Время полного растворения определяется из условия ![]() (частица полностью растворилась):
(частица полностью растворилась):
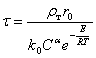 (32)
(32)
Доля нерастворившегося продукта ![]() определяется очевидным соотношением
определяется очевидным соотношением 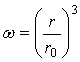 , с учетом которого уравнение (31) можно записать так:
, с учетом которого уравнение (31) можно записать так:
![]() (33)
(33)
Характеристические графические зависимости ![]() для разных С и Т представлены на рис.3.
для разных С и Т представлены на рис.3.
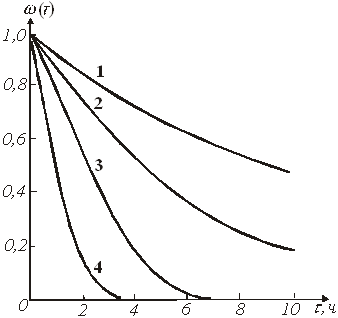
Рис.3. Зависимость доли нерастворившегося компонента от времени при различных условиях для продукта, состоящего из полностью растворившихся сферических частиц.
Температура: ![]() . Концентрация моль/л:
. Концентрация моль/л: ![]()
С учетом выражения (32) последнее уравнение можно переписать в виде 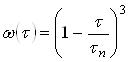 или:
или:
![]() (34)
(34)
Сравнение уравнений (33) и (34) показывает, что кинетическая характеристика ![]() зависит от температуры и концентрации активного реагента, тогда как кинетическая функция
зависит от температуры и концентрации активного реагента, тогда как кинетическая функция ![]() не содержит этих величин в явном виде. Может показаться, что преимущество, связанное с инвариантностью кинетической функции относительно С и Т, является до некоторой степени фиктивным: вместо единственной характеристики
не содержит этих величин в явном виде. Может показаться, что преимущество, связанное с инвариантностью кинетической функции относительно С и Т, является до некоторой степени фиктивным: вместо единственной характеристики ![]() мы имеем две характеристики
мы имеем две характеристики ![]() и
и ![]() , причем вторая из них по прежнему зависит от условий растворения.
, причем вторая из них по прежнему зависит от условий растворения.
Однако мы заменили бесчисленное множество функций ![]() , зависящих от двух параметров С и Т, единственной функцией
, зависящих от двух параметров С и Т, единственной функцией ![]() . Что же касается полного растворения
. Что же касается полного растворения ![]() , то эта величина служит масштабным коэффициентом, позволяющим перейти от безразмерного времени х к натуральному:
, то эта величина служит масштабным коэффициентом, позволяющим перейти от безразмерного времени х к натуральному: ![]() . Разумеется, для любого сочетания С и Т этот коэффициент имеет определенное значение, устанавливаемое экспериментально или теоретически (при известной модели растворения).
. Разумеется, для любого сочетания С и Т этот коэффициент имеет определенное значение, устанавливаемое экспериментально или теоретически (при известной модели растворения).
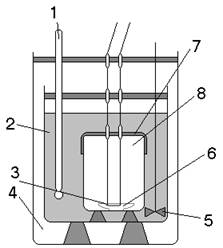
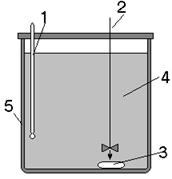
Исходный продукт, как и в предыдущем случае, представляет собой (рис.4) совокупность сферических частиц одинакового радиуса r0. Частицы состоят из растворимого вещества и инертного материала. Выщелачивание частицы происходит таким образом, что в любой момент времени внутри частицы имеется сферическое ядро радиуса r, окруженное слоем пористого инертного материала. Такое явление вполне вероятно, когда исходная частица является пористой и состоит из не менее чем из двух веществ, одно из которых в данных условиях не растворяется. При этом нерастворяющееся вещество образует так называемый "пористый скелет". Возможен также случай, когда химически растворяющееся вещество образует два продукта, один из которых нерастворим в данных условиях. Например, растворение молекулы хрикозолы в серной кислоте:
![]()
Образующийся гель ![]() покрывает пористым сферическим слоем растворяющуюся частицу хрикозолы. Через этот слой диффундирует серная кислота к поверхности растворения и обратно диффундирует
покрывает пористым сферическим слоем растворяющуюся частицу хрикозолы. Через этот слой диффундирует серная кислота к поверхности растворения и обратно диффундирует ![]() .
.

Рис.4. Модель выщелачиваемой частицы
Радиус ядра r уменьшается по мере выщелачивания, а наружный радиус частицы r0 остается неизменным (или условно-неизменным). Скорость выщелачивания определяется диффузией реагента сквозь поры инертного слоя и описывается уравнением одномерной сферической диффузии:
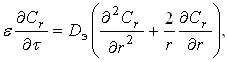 (34)
(34)
где ![]() - порозность инертного слоя;
- порозность инертного слоя;
![]() - эффективный коэффициент диффузии;
- эффективный коэффициент диффузии;
![]() - концентрация диффундирующего вещества на расстоянии r от центра частицы.
- концентрация диффундирующего вещества на расстоянии r от центра частицы.
Как уже отмечалось, наибольший интерес представляет кинетические характеристики продукта при постоянных температуре и концентрации активного реагента в объеме раствора. Преобразование уравнения (34) приводит к следующему результату:
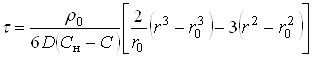 (35)
(35)
Учитывая, что 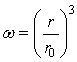 , можно это уравнение переписать так:
, можно это уравнение переписать так:
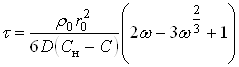 (36)
(36)
При полном извлечении ![]() , поэтому:
, поэтому:
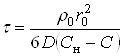 (37)
(37)
Разделив уравнение (36) на (37) получим связь между безразмерным временем х и долей нерастворившегося компонента ![]() :
:
![]() (38)
(38)
Уравнение (36) представляет в неявном виде кинетическую характеристику ![]() . Мы снова видим, что эта характеристика зависит от концентрации и температуры (через коэффициент диффузии и концентрации насыщенного раствора), тогда как кинетическая функция
. Мы снова видим, что эта характеристика зависит от концентрации и температуры (через коэффициент диффузии и концентрации насыщенного раствора), тогда как кинетическая функция ![]() , определяется уравнением (38) и не зависит от С, и Т.
, определяется уравнением (38) и не зависит от С, и Т.
![]() (39)
(39)
Тогда:
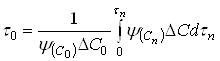 (40)
(40)
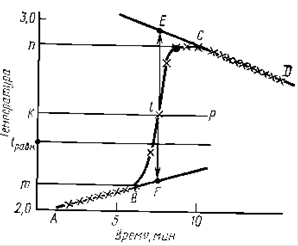
Входящий в уравнение (40) интеграл численно равен площади под нижней кривой рис.5, если принять, что ![]() об/мин. Таким образом, результаты периодического опыта, проведенного при изменяющейся концентрации С0, позволяют легко определить время
об/мин. Таким образом, результаты периодического опыта, проведенного при изменяющейся концентрации С0, позволяют легко определить время ![]() , относящейся к постоянному значению концентрации С0. Нам, однако, нужно знать время полного растворения
, относящейся к постоянному значению концентрации С0. Нам, однако, нужно знать время полного растворения ![]() и при других сочетаниях С, n и Т.
и при других сочетаниях С, n и Т.
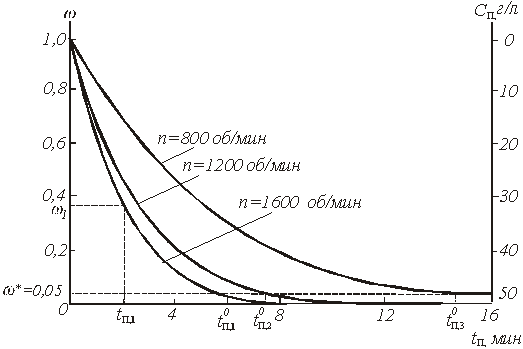
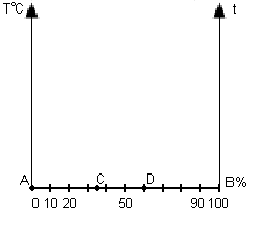
Рис.5. Зависимость доли нерастворившегося продукта ![]() и концентрации раствора Сn от времени
и концентрации раствора Сn от времени ![]() при растворении бихромата калия в воде в условиях периодического опыта
при растворении бихромата калия в воде в условиях периодического опыта
Связь между ![]() и
и ![]() легко установить с помощью уравнения:
легко установить с помощью уравнения:
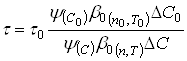 (41)
(41)
Входящая в уравнение (41) функция ![]() определяется экспериментально.
определяется экспериментально.
Разность концентраций обычно известна: ![]() или
или ![]() . Поэтому для выполнения расчетов по уравнению (41) нам нужно научиться определять значение коэффициента
. Поэтому для выполнения расчетов по уравнению (41) нам нужно научиться определять значение коэффициента ![]() или отношение
или отношение 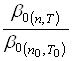 . Если сравнивать скорости растворения в двух опытах, отличающихся температурой и числом оборотов мешалки, то для разных значений
. Если сравнивать скорости растворения в двух опытах, отличающихся температурой и числом оборотов мешалки, то для разных значений ![]() в первом и втором опытах можно записать:
в первом и втором опытах можно записать:
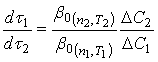 (42)
(42)
Уравнение (42) относится к произвольному но фиксированному значению ![]() . Производная
. Производная ![]() и разности концентраций
и разности концентраций ![]() и
и![]() относится к точке, отвечающей этому значению
относится к точке, отвечающей этому значению ![]() .
.
В следующих двух случаях интегрирование уравнения (42) приводит к линейной зависимости ![]() от
от ![]() . Графический вариант определения
. Графический вариант определения ![]() для различных оборотов мешалки иллюстрируется рис.6. и аналогичен описаному в разделе 2.2. для определения порядка реакции.
для различных оборотов мешалки иллюстрируется рис.6. и аналогичен описаному в разделе 2.2. для определения порядка реакции.
Если скорость растворения определяется скоростью диффузии реагента из объема к межфазной поверхности (т.е. если ![]() ), то для двух опытов с одинаковой начальной концентрацией активного реагента справедливо равенство
), то для двух опытов с одинаковой начальной концентрацией активного реагента справедливо равенство ![]() .
.
Тогда:
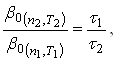 (43)
(43)
где ![]() и
и ![]() означает время, необходимое для достижения одного и того же значения
означает время, необходимое для достижения одного и того же значения ![]() в первом и втором опытах.
в первом и втором опытах.
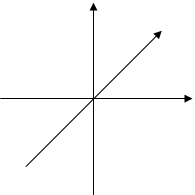
Уравнение (43) показывает, что зависимость ![]() от
от ![]() есть прямая линия, угловой коэффициент которой равен отношению
есть прямая линия, угловой коэффициент которой равен отношению 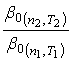 . Поэтому, если
. Поэтому, если ![]() , для определения отношения коэффициентов
, для определения отношения коэффициентов ![]() достаточно провести два периодических опыта с одинаковой начальной концентрацией активного реагента, но при разных температурах Т и Т0 и числом оборотов мешалки n и n0. Затем нужно найти угловой коэффициент зависимости
достаточно провести два периодических опыта с одинаковой начальной концентрацией активного реагента, но при разных температурах Т и Т0 и числом оборотов мешалки n и n0. Затем нужно найти угловой коэффициент зависимости ![]() от
от ![]() .
.
Оптимальную температуру процесса определяют в предварительных опытах. Отношение коэффициентов ![]() при одинаковых значениях температуры Т0 и различных числах оборотов n1 и n2 определяется по формуле:
при одинаковых значениях температуры Т0 и различных числах оборотов n1 и n2 определяется по формуле:
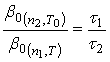 (44)
(44)
Это уравнение справедливо не только при ![]() , но и в тех случаях, когда
, но и в тех случаях, когда ![]() .
.
На рис.7 показаны экспериментальные данные, а на рис.8 результаты их обработки. После проведения опытов в широком интервале изменения чисел оборотов мешалки, вычисления ![]() для любых значений технологических параметров легко осуществить по формуле (41).
для любых значений технологических параметров легко осуществить по формуле (41).
Определение ![]() при температуре Т, концентрации С и числе оборотов n в случае, когда
при температуре Т, концентрации С и числе оборотов n в случае, когда ![]() , осуществляют по формуле:
, осуществляют по формуле:
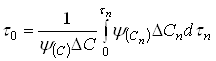 , (45)
, (45)
где ![]() - время полного растворения в периодическом опыте при температуре Т и числе оборотов n;
- время полного растворения в периодическом опыте при температуре Т и числе оборотов n;
![]() - текущая концентрация в этом опыте.
- текущая концентрация в этом опыте.
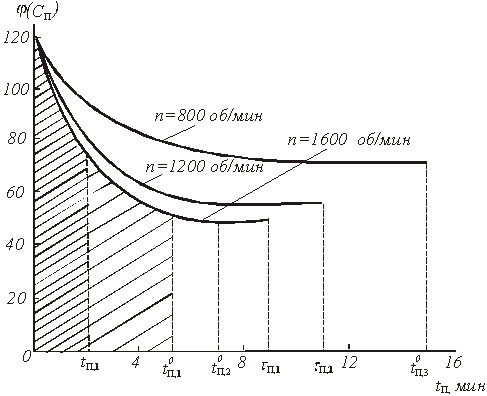
Рис.6. К графическому определению кинетической функции растворения соли в воде, используя экспериментальные данные рис.5
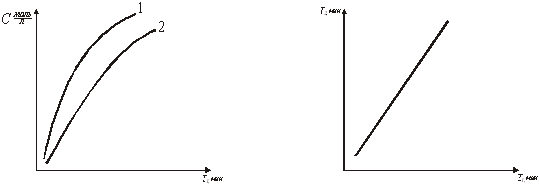
Рис.7. Результаты опытов по растворению Рис.8. График для опр деления ![]() соли в воде. Скорость вращения при двух различных скоростных мешалки (об/мин): 1-2000; 2-1000.вращений мешалки.
соли в воде. Скорость вращения при двух различных скоростных мешалки (об/мин): 1-2000; 2-1000.вращений мешалки.
Определенные в лабораторных условиях кинетическая функция ![]() , время полного растворения
, время полного растворения ![]() , коэффициент массопередачи
, коэффициент массопередачи ![]() и его зависимость от числа оборотов используются при моделировании промышленных реакторов.
и его зависимость от числа оборотов используются при моделировании промышленных реакторов.
Похожие работы
... циклов. Как уже было отмечено, калориметрия используется для определения тепловых эффектов реакций, в частности она используется и для определения теплот растворения солей или других соединений в воде или других растворителях. Это является одной из самых интересных задач термохимии, так как выделение теплоты при растворении солей может быть использовано для разогрева или охлаждения тех или иных ...
... или кислот; так получают, например, золь гидроксида железа(III), имеющий следующее строение: {[Fe(OH)3]m n FeO+ · (n–x)Cl–}x+ x Cl– 4.2.2 Агрегативная устойчивость лиофобных коллоидов. Строение коллоидной мицеллы Лиофобные коллоиды обладают очень высокой поверхностной энергией и являются поэтому термодинамически неустойчивыми; это делает возможным самопроизвольный процесс уменьшения ...
... с кислородом, восстановлением - отнятие кислорода. С введением в химию электронных представлений понятие окислительно-восстановительных реакций было распространено на реакции, в которых кислород не участвует. В неорганической химии окислительно-восстановительные реакции (ОВР) формально могут рассматриваться как перемещение электронов от атома одного реагента (восстановителя) к атому другого ( ...
... реакции на альдегидную группу – окисляется оксидом серебра (1), присоединяет синильную кислоту (4): Химические свойства: 1. 2. 3. 4. 5. 6. 7. 8. Спиртовое брожение. Эта реакция характерна для гексоз. Она осуществляется с помощью биологических катализаторов – ферментов. При сбраживании гексозы превращаются в этиловый спирт. Для пентоз брожение ...

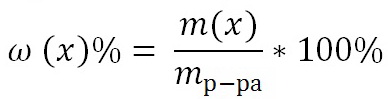
0 комментариев