Навигация
4.6 Задача
Дана улитка Паскаля с полюсом в точке O. Написать уравнения в прямоугольной и полярной системах координат.
Решение:
Пусть начало координат – в полюсе O, ось OX направлена по лучу OB. Тогда уравнение в прямоугольной системе координат будет иметь вид:
![]() . (1)
. (1)
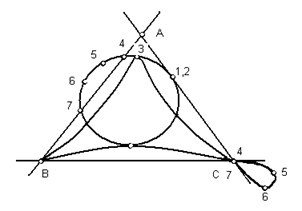
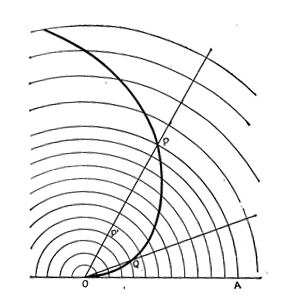
Строго говоря, это уравнение представляет фигуру, состоящую из улитки Паскаля и полюса O, который может и не принадлежать определенному выше геометрическому месту (такой случай имеет место для линий 3 и 4 на рис.6).
Уравнение в полярной системе (O – полюс, OX – полярная ось):
![]() , (2)
, (2)
где ![]() меняется от какого-либо значения
меняется от какого-либо значения ![]() до
до ![]() .
.
5. Лемниската Бернулли
5.1 Определение
Лемниската есть геометрическое место точке, для которых произведение расстояний от них до концов данно отрещка ![]() равно
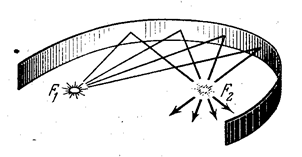
равно ![]() . Точки F1, F2 называются фокусами лемнискаты; прямая F1F2 – ее осью.
. Точки F1, F2 называются фокусами лемнискаты; прямая F1F2 – ее осью.
5.2 Исторические сведения
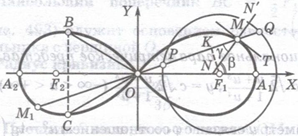
В 1694 г. Якоб Бернули в работе, посвященной теории приливов и отливов, использовал в качестве вспомогательного средства линию, которую он задает уравнением ![]() . Он отмечает сходство этой линии (рис.8) с цифрой 8 и узлообразной повязкой, которую он именует «лемниском». Отсюда называние лемниската. Лемниската получила широкую ивестность в 1718 г., когда итальянский математик Джулио Карло Фаньяно (1682 – 1766) установил, что интеграл, представляющий длину дуги лемнискаты, не выражается через элементарные функции, и тем не менее лемнискату можно разделить (с помощью линейки и циркуля) на n равных дуг при условии, что
. Он отмечает сходство этой линии (рис.8) с цифрой 8 и узлообразной повязкой, которую он именует «лемниском». Отсюда называние лемниската. Лемниската получила широкую ивестность в 1718 г., когда итальянский математик Джулио Карло Фаньяно (1682 – 1766) установил, что интеграл, представляющий длину дуги лемнискаты, не выражается через элементарные функции, и тем не менее лемнискату можно разделить (с помощью линейки и циркуля) на n равных дуг при условии, что ![]() или
или ![]() или
или ![]() , где m – любое целое положительное число.
, где m – любое целое положительное число.
Лемниската есть частный вид линии Кассини. Однако, хотя линии Кассини получили всеобщую известность с 1749 г., тождественность «восьмерки Кассини» с лемнискатой Бернули была уставновлена лишь в 1806 г. (итальянским математиком Саладини).
5.3 Построение
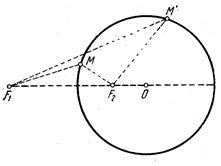
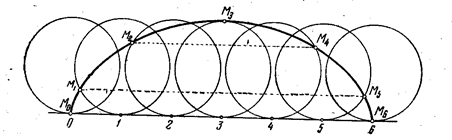
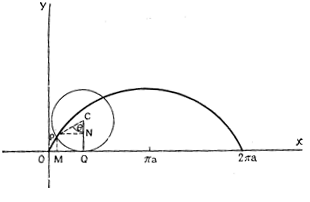
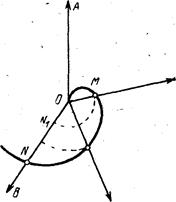
Можно применять общий способ построя линия Кассини, но нижеизложенный способ (К. Маклорена) и проще и лучше. Строим (см. рис.) окружность радиуса ![]() с центром в точке F1 (или F2). Проводим произвольную секущую OPQ и откладываем на этой прямой в обе стороны от точки O отрезки OM и OM1, равные хорде PQ. Точка M опишет одну из петель лемнискаты, точка M1 – другую.
с центром в точке F1 (или F2). Проводим произвольную секущую OPQ и откладываем на этой прямой в обе стороны от точки O отрезки OM и OM1, равные хорде PQ. Точка M опишет одну из петель лемнискаты, точка M1 – другую.
5.4 Особенности формы
Лемниската имеет две оси симметрии: прямую F1F2 (OX) и прямую OY![]() OX. Точка O – узловая; обе ветви имеют здесь перегиб. Касательные в этой точке составляют с осью OX углы
OX. Точка O – узловая; обе ветви имеют здесь перегиб. Касательные в этой точке составляют с осью OX углы ![]() . Точки A1,A2 лемнискаты, наиболее удаленные от узла O (вершины лемнискаты), лежат на оси F1F2 на расстоянии
. Точки A1,A2 лемнискаты, наиболее удаленные от узла O (вершины лемнискаты), лежат на оси F1F2 на расстоянии ![]() от узла.
от узла.
5.5 Свойства нормали.
Подяоный радиус OM лемнискаты образует с нормалью MN угол ![]() , вдвое больше полярного угла
, вдвое больше полярного угла ![]() :
:
![]() .
.
Другими словами: угол ![]() между осью OX и вектором NN' внешней нормали лемнискаты в точке M равен утроенному полярному углу точки M:
между осью OX и вектором NN' внешней нормали лемнискаты в точке M равен утроенному полярному углу точки M:
![]() .
.
5.6 Построение касательной
Чтобы построить касательную к лемнискате в ее точке M, проводим полярный радиус OM и строим ![]() . Перпендикуляр MT к прямой MN есть искомая касательная.
. Перпендикуляр MT к прямой MN есть искомая касательная.
5.7 Задача
Написать уравнение лемнискаты Бернулли в прямоугольной системе координат (O – серидина отрезка F1F2) и в полярной системе координат (O – полюс).
Решение:
Пусть точка O – начало координат ; ось OX направлена по F1F2. Тогда Уравнение в прямоугольной системе координат:
![]() .
.
Если O – полюс, OX – полярная ось, то уравнение в полярной системе:
![]() .
.
Угол ![]() изменяется в промежутках
изменяется в промежутках ![]() и
и ![]() .
.
Заключение
В данной работе мы рассмотрели некоторые замечательные кривые, изучили их способы построения, особенности формы и задачи, связанные с этими кривыми.
В параграфе 1 была рассмотрена строфоида, особенности её формы, стереометрическое образование и исторические сведения.
Во 2-м параграфе мы изучили циссоиду Диокла и некоторые формулы, связанные с ней.
В параграфе 3 узнали метод построения, особенности формы и исторические сведения о кривой, называемой «Декартов лист».
В 4-м параграфе рассмотрели улитку Паскаля. Её определение, построение, особенности формы, свойства нормали и построение касательной.
В параграфе 5 была изучена лемниската Бернулли: определение, построение, исторические сведения, особенности формы, свойства нормали и построение касательной.
А также при помощи задач узнали формулы кривых в прямоугольной декартовой и полярной системах координат.
Используемая литература:
1. Маркушевич А.И., Замечательные кривые, М., 1978 г., 48 стр. с ил.
2. Выгодский М.Я., Справочник по высшей математике, М.: АСТ: Астрель, 2008, 991 стр. с ил.
3. Атанасян Л.С. и Атанасян В.А., Сборник задач по геометрии. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов. Ч. I, М., "Просвещение", 1973, 256 с.
4. Гурова А.Э. Замечательные кривые вокруг нас. М, 1989
5. Маркушевич А.И. Замечательные кривые. - М, 1978
6. http://ru.wikipedia.org/wiki/Строфоида
7. http://ru.wikipedia.org/wiki/Лемниската_Бернулли
8. http://ru.wikipedia.org/wiki/Улитка_Паскаля
Похожие работы
... этим лучом и касательной к спирали, проведенной в точке пересечения (Рис. 13). Теорема Паскаля Б. Паскалю (1623—1662) не было еще и 17 лет, когда он открыл замечательное общее свойство конических сечений. Об его открытии математикам поведала афиша, отпечатанная в количестве 50 экземпляров; только два из них дошли до нашего времени. Несколько таких афиш были расклеены на стенах домов и церквей ...
... , повысить интерес к учению; 3) углубить знания, полученные на уроках математики. Ход занятия I. Организационный момент II. Основная часть 1) Лекция об истории изучения плоских кривых [см. гл. I § 1] 2) Задание Ребята, разгадаем с вами кроссворд: ПАСКАЛЬ ПАПИРУС АПОЛЛОНИЙ РОБЕРВАЛЬ АРХИМЕД ГЕОМЕТРИЯ По горизонтали 1. Учёный, считавший, что дуга спирали ...
... различных видах деятельности; • развитии пространственного воображения и пространственных представлений, образного, пространственного, логического, абстрактного мышления школьников; • формировании умений применять геометро-графические знания и умения для решения различных прикладных задач; • ознакомлении с содержанием и последовательностью этапов проектной деятельности в области технического и ...
... , поскольку точки М и М’ входят в формулу равноправно, а для центра инверсии и бесконечно удаленной области все очевидно. 1.3. Формула инверсии в комплексно сопряженных координатах. Найдем формулу обобщенной инверсии при задании точек комплексными числами. Пусть точкам S, M и М’ соответствуют комплексные числа s, z и z’. По формуле скалярного произведения векторов . Коллинеарность точек S, M и ...



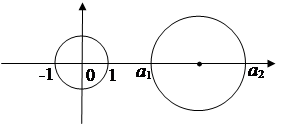

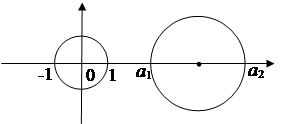
0 комментариев